What Is 4/3 as a Decimal + Solution With Free Steps
The fraction 4/3 as a decimal is equal to 1.33.
The ratio of two whole numbers represented as p/q is known as a Fraction. The p component is referred to as the Numerator and the q component as the Denominator, while p/q stands for p number of pieces out of total q pieces.
The numerator and denominator are two components of a fraction that are distinguished by a line between them. The number placed above the line is known as the Numerator, whereas the number placed below the line is the Denominator. Fractions can easily be solved using Division to find their equivalent decimal value.
Here, the decimal equivalent of 4/3 will be computed using the Long Division method.

Solution
To solve a fraction, we have to transform it into a division by separating its components according to the nature of their functions. The numerator is referred to as the Dividend and is divided by the denominator, also known as the Divisor. In the given example, we have 4 and 3 as dividend and divisor, respectively.
Mathematically, we can state that:
Dividend = 4
Divisor = 3
Two more terms are important to understand the process of division. These are quotient and remainder. The Quotient is the equivalent value of a fraction that we get as a result of division. However, if a fraction undergoes partial division, the remaining term is known as Remainder.
Quotient = Dividend $\div$ Divisor = 4 $\div$ 3
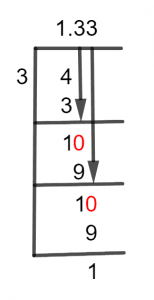
Figure 1
4/3 Long Division Method
The solution of 4/3 using Long Division is shown below:
4 $\div$ 3
To get the solution of a fraction, first, we see which is greater among the numerator and denominator. If the denominator is greater, then we must introduce a Decimal point. However, if the numerator is greater, we can proceed without it.
In the above fraction, 4 is greater than 3, so we will divide 4 by 3.
4 $\div$ 3 $\approx$ 1
Where:
3 x 1 = 3
The remainder is computed by subtracting the two quantities as:
4 – 3 = 1
As we have obtained a non-zero remainder, which is less than the divisor, so now we have to use a decimal Point. Adding a zero to the right of the remainder inserts a decimal point in the quotient and the remainder becomes 10, which is to be divided by 3.
10 $\div$ 3 $\approx$ 3
Where:
3 x 3 = 9
The remainder is given as:
10 – 9 = 1
We get 1 as a remainder again, so we insert a zero to its right again and make it 10. But this time, we don’t insert any decimal point in the quotient, because it already contains one. 10 is again to be divided by 3. Therefore, mathematical calculations are the same as that in the previous step.
Finally, we have a Remainder of 1 and a Quotient of 1.33. It shows that 4/3 is a non-terminating fraction.
Images/mathematical drawings are created with GeoGebra.
