What Is 7/11 as a Decimal + Solution With Free Steps
The fraction 7/11 as a decimal is equal to 0.636.
Fractions are converted into decimal values to make them easier to understand. Fractions are generally represented in p/q form. The p in the fraction is referred to as the numerator, while the q is known as the denominator of the fraction. Both the numerator and the denominator are separated by a line called the division line.
The division operator is used to solve the fraction, and it appears to be the most difficult of all mathematical operators, but we can make it easier by using the Long Division method, which is simple and convenient.
So we can convert the given fraction 7/11 into its decimal value by using the long division method.
Solution
Before starting a solution for the given fraction, we will first explain the important terms used in the long division method. The terms are “Dividend” and “Divisor.”
The numerator in a fraction is known as the dividend while the denominator is referred to as the divisor, or we can also explain to them as, for p/q, p is for the dividend while q is referred to as the divisor.
Dividend = 7
Divisor = 11
When we solve a mathematical problem, we end up having some result, and when we solve a fraction by using the long division method, the result is referred to as the Quotient. It is the answer of a fraction in decimal form.
Quotient = Dividend $ \div $ Divisor = 7 $ div $ 11
The solution through the long division is as shown below:
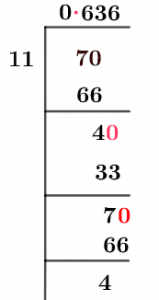
Figure 1
7/11 Long Division Method
We have a fraction:
7 $ \div $ 11
When we calculate fractions, there are two possible results: greater than one and less than one. The numerator and denominator both matter. Our result will be greater than one if the numerator is greater than the denominator.
Similar to this, if the fraction’s numerator is less than its denominator, the result will be less than one. Therefore, in this situation of 7/11 when the numerator is less than the denominator, it is clear that the result will be less than one.
Another concept that must be defined in this context is the concept of a remaining number, which results from the division of two non-completely divisible integers. And that number is referred to as the Remainder.
We will first add a decimal point to the quotient of the provided fraction, which will add zero to the dividend’s right and give us a dividend of 70.
So now, by adding a zero to the dividend, we have 70.
70 $ \div $ 11 = 6
Where:
11 x 6 = 66
Therefore the remainder is 70 – 66 = 4. Now again adding a zero will make 4 as 40 and divisible by 11.
40 $ \div $ 11 $\approx$ 3
11 x 3 = 33
Now the remainder is 40 – 33 = 7. Again 7 is smaller than 11 adding a zero gives 70 and makes it divisible by 11.
70 $ \div $ 11 $\approx$ 6
11 x 6 = 66
The remainder of the division is 4.
So the resulting Quotient is 0.636 for the fraction of 7/11, with 4 as a remainder.
Images/mathematical drawings are created with GeoGebra.
