What Is 8/5 as a Decimal + Solution With Free Steps
The fraction 8/5 as a decimal is equal to 1.6.
We determine how many equally sized pieces we can divide a number or quantity into using the mathematical idea of Fractions. In its depiction, a line separates the Numerator and Denominator, which are its two parts.
Since Decimals are more convenient and understandable than fractions, so mostly fractions are converted into decimal forms before using in mathematical operations. There are various methods to do this conversion, but mostly Long Division is preferred.
This article will provide the details of the Long Division method.
Solution
When we divide a fraction into its parts based on how they operate, we transform it into division. Consequently, we find the numerator to be the Dividend, a number we have to divide, and the denominator to be the Divisor, a number that will divide.
Thus, in our example of 8/5, we have numerator 8 as a dividend and denominator 5 as a divisor.
Dividend = 8
Divisor = 5
The complete division of two numbers gives us a decimal value equivalent to a fraction named the Quotient. However, there are instances where two integers cannot split evenly and leave us with some value. The remainder is the name of this value.
Quotient = Dividend ÷ Divisor = 8 ÷ 5
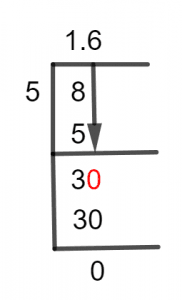
Figure 1
8/5 Long Division Method
We have two important divisional rules. The first rule indicates that we must subtract a multiple of the Divisor closest to the Dividend from the Dividend. Two numbers have been divided completely if there is no value left after subtraction. On the other hand, a leftover value means that we still need to solve it.
According to the second rule, we put a Decimal Point in the Quotient whenever the Dividend is lesser than the Divisor. However, in this case where the Dividend is bigger, no decimal point is needed.
Our task is to solve the following fraction:
8 ÷ 5
Given that our dividend 8 is higher than our divisor 5, we must solve an improper fraction. We can therefore continue our division without using a decimal point. 8 is split by 5 as follows:
8 ÷ 5 \approx 1
5 x 1 = 5
By subtracting 5 from 8, we can find the remaining term.
8 – 5 = 3
As a result, the remainder is now smaller than the Divisor. For our computations to be complete, we need a decimal point. We can get this decimal point by multiplying our remainder by 10. The remainder 3 thus gives us 30 and serves as our Dividend for the subsequent iteration.
30 ÷ 5 \approx 6
5 x 6 = 30
30 – 30 yields zero. This gives us the conclusion that the fraction is divided, and we get 1.6 as the Quotient and an equivalent decimal of 8/5.
Images/mathematical drawings are created with GeoGebra.
