What Is 9/2 as a Decimal + Solution With Free Steps
The fraction 9/2 as a decimal is equal to 4.5.
A Fraction is used to express how many identical parts there are in a whole. It consists of two numbers expressed as p/q. Here, p stands for the fraction’s Numerator, q for its Denominator, and the line represents the Division between p and q.
Because of their ease of understanding and use in mathematical calculations, decimals are typically used to convert fractions. Furthermore, it is difficult to find the largest or smallest number by comparing two fractions but it becomes very easy when we deal with their decimal values.
The conversion of a fraction 9/2 by using the method of Long Division is shown below.
Solution
Checking if a fraction is a Proper or an Improper Fraction is the first step to its solution. In contrast to an improper fraction, which has a larger numerator than the denominator, a proper fraction contains a greater denominator.
A fractional problem is changed into a division problem to solve it. This is accomplished by categorizing its constituent parts or elements based on how they function. The Dividend is the denominator or the number that will be split, while the denominator is the term used to describe the Divisor.
Dividend = 9
Divisor = 2
We obtain the Quotient, which is our outcome after the division procedure is complete. However, if two numbers are not completely divided, we obtain a value known as the Remainder.
Quotient = Dividend $\div$ Divisor = 9 $\div$ 2
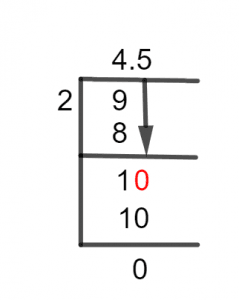
Figure 1
4 1/2 Long Division Method
The division of 9 by 2 by the Long Division method is shown below.
9 $\div$ 2
When we have an improper fraction like 9/2, we don’t require a Decimal Point. So, for this division, we have to determine the multiple of 2, which is closest to 9, so that it can be subtracted from 9 to compute the remainder. The multiple of 2 that is closest to 9 is 8, thus we can write the mathematical steps as:
9 $\div$ 2 $\approx$ 4
Where:
2 x 4 = 8
1 is left behind and is referred to as the remainder.
9 – 8 = 1
Now it can be seen that divisor 2 has a greater value than the remainder 1, so to proceed with the division process, therefore, now we should have a Decimal Point. This decimal point is obtained by multiplication of the remainder with 10. Hence, we get 10 to divide by 2.
10 $\div$ 2 $\approx$ 5
Where:
2 x 5 = 10
Now, we have no left-over value.
10 – 10 =0
As we get zero remaining value when both the divisor and the quotient are factors of the dividend, so we can say that 9 is completely divided by 2 and the value of the Quotient is 4.5.
Images/mathematical drawings are created with GeoGebra.
