Girard Desargues’s Phenomenal Contributions To Geometry

Rome wasn’t built in a day, so goes the cliché, and it wouldn’t be out of place to say that mathematics and geometrics weren’t developed in a day either. Notable men of honor have helped in propagating both field of knowledge.

This article is about one of the most phenomenal contributors in the field of Geometry, Girard Desargues, whose contribution to the area of Synthetic Projective Geometry remains a remarkable achievement.

Desargues Theorem, an approach to Projective Geometry through the study of figures and shapes, is an acknowledged and improved version to the work of previous contributors such as Pappus and Apollonius and a continuation of the Euclidean Geometry.

Girard Desargues was born on the 21 of February 1591 in Lyon, to a wealthy French aristocrat. His father was a notary public for the crown. The most famous work of Desargues in the field of geometry. Rough draft for an essay on the result of taking plane sections of a cone was printed only in small quantities in 1639.

With this Mathematical statement publication, he was able to introduce his unique form of Geometry, “The Desargues Theorem,” into Mathematics, which motivated the development of Projective Geometry in the first quarter of the 19th century by another French mathematician, Jean-Victor Poncelet. This feat has made many regard Desargues has the founder of Projective Geometry.

Desargues, in his early life, served in the French royal army, worked as a tutor, an engineer, an architect and a consultant in the entourage of Richelieu. Still, he was more known for his architectural and engineering skills.

As an engineer, Desargues used the principle of the Epicycloid wheel, a law that was relatively unknown at that time to design and install a system for lifting water near Paris. Several friends who were also members of Marin Mersenne’s mathematical circle which included, Rene Descartes, Blaise Pascal and his father, Étienne Pascal influenced Desargues to stay in Paris, and most of the Desargues works were limited to their suggestions and opinions.

Desargues works were dense and theoretical in their approach; his works dealt with the practical application of his theorem. The Perspective, which was written in 1636, Sundials and the cutting of stones for use in building in 1640 are all theoretical writings that practically addressed the application of some of his principles to the cutting of stones used in building complex structures.

Desargues’s work on Perspective projection, as at when he published his writing, is a climax of years of research and enquiry across the classical era in visual research that goes beyond the renaissance perspective theories. Desargues Projective Geometry, where objects appear deformed based on the point of view, is a continuation of the Euclidean Geometry, which states parallel lines of infinite size do vary if proportion and sharp are put into consideration.

Most regard Projective Geometry as one of Desargues’ most famous work. However, only one copy of the very dense and short book is known to survive. The books start with lines and range of complexity points located on edge, which explains the properties that are invariant under projection using the comics and infinite distance concept.

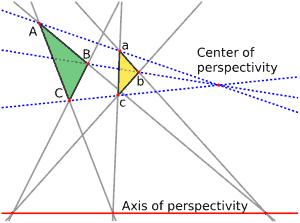Corresponding sides of a line or triangle, when extended on the same line, would inevitably meet at a point called the Axis of Perspectivity. At the same time, the centre of perspectivity are lines that meet after running through a corresponding line on a triangle. Desargues theorem appeared in an appendix entitled Universal Method of M. Desargues for Using Perspective. Abraham Bosse also published the Desargues perspective theorem in work on Perspective in 1648.

The Desargues theorem of projective geometry states that the intersection points of two triangles ABC and a’b’c, which are the corresponding side lies on a straight line and related to each other in a visible way from one point. It means the lines AA′, BB′, and CC′ all intersect in one end, which is in the corresponding side that lies on a straight line when the connecting paths of corresponding vertices cross in one point and vice versa.

But if two similar lines are parallel; then there would be only two points of intersection instead of a three, and the theorem must be modified to reflect the result. Several mathematicians such as Abraham Bosse, who taught based on the Desargues method, found Desargues work to be intriguing and went on to publish a more acceptable presentation of this method.

As earlier stated, Desargues’s theorem of Projective Geometry has only been studied with a three-dimensional triangle. The proof of plane perspective geometry requires two-dimensional triangles that are on separate planes but can also be proven in more than two dimensions from other verified theories in Projective Geometry.

The Desargues theorem was named after him for several reasons, one of which could be because he was able to effectively link perspectivity from a point and perspectivity from a line, which are both two different aspects of projective geometry. Even though one of his significant works Brouillion project was relatively unknown for a long-time till 1845 when another French mathematician Michel Charles discovered it.

In the 17th century, Rene Descartes Algebra approach Discours de la méthode published in 1637 was a preferred approach geometry, and it dominated the era.

Descartes approach made Desargues theorem which was a new approach to the study of figures through their projection become redundant and eventually out of space, even though it was appreciated by famous mathematicians such as Blaise Pascal and Gottfried Wilhelm Leibniz.

Desargues theorem was later rediscovered and republished in 1864. Several mathematicians such as Gaspard Monge have reinvented Projective Geometry, which is an improvement of descriptive geometry and its perspective techniques in honor of Desargues’s contribution to the field.

Hexagons theorem according to Pappus theorem states that if a hexagon AbCaBc is drawn in the same line, where vertices a, b, and c are on the same line, and vertices A, B and C are on the second line. Then every two opposite sides of the hexagon lie on two lines that meet at a point.

This theorem also goes for three points of construction, which are collinear. Heisenberg 1950 believes the Desargues theorem was deduced from the application of pappus theorem. However, not all Desargues planes are pappus because they don’t satisfy pappus theorem principles, but the influence of pappus theorem in the Desargues theorem is undeniable.

Despite the acknowledged importance of Desargues in the history of geometry, it is evident that several mathematicians such as Apollonius and Pappus through their previous publications, remarks and works had a significant influence on Desargues’ practices.

Desargues’s theorem has been reinvented into a more straightforward and relatable projective space, and this has paved the way for the publication of other hypotheses within this framework. The new interpretation is more straightforward in terms of their approach to intersections of lines, collinearity of points, measurement of distance and angles and similarities of shapes.

Conclusively, Desargues’s name has been etched on a golden plaque in the field of Geometry. Although, further adjustments might still be made to his notable theorem in the future as human’s understanding of the concepts improves. His contribution to this field of knowledge remains equally significant and evergreen.