Brackets|Definition & Meaning

Figure 1 shows different types of brackets in a numeric expression. 

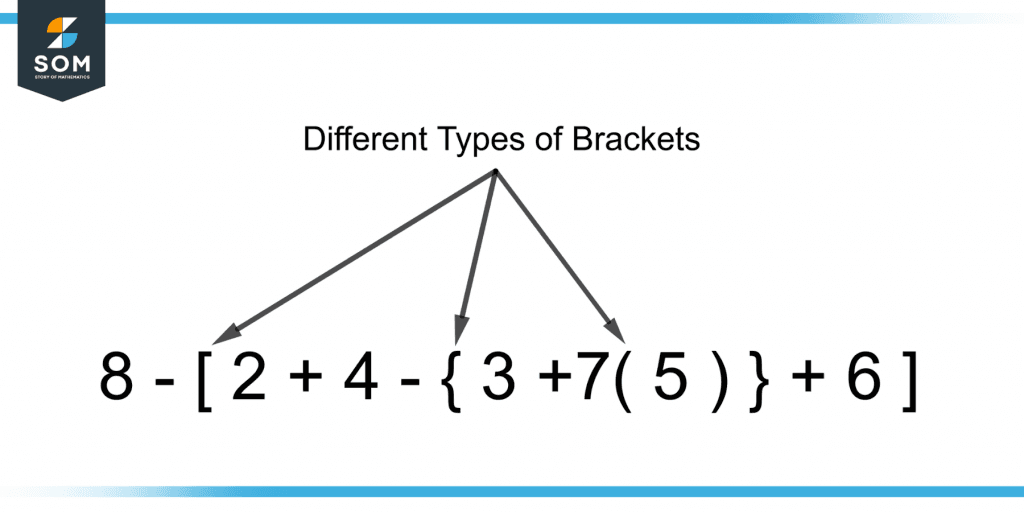
Figure 1 – Different Types of Brackets in a Numeric Expression

Note that each bracket has an opening end and a closing end.

Importance of Brackets

Brackets play an essential role in solving algebraic equations as they provide a systematic way to solve the equation. Without brackets, solving the mathematical expression would be confusing and quite tedious.

Types of Brackets

Brackets are organizational tools used to define the order of operation in an algebraic equation. The different variety of brackets makes the algebraic expression look more comprehensible for solving it.

The different types of brackets are given as follows:

Round Brackets

Round Brackets are also known as parentheses, circle brackets, parens, or smooth brackets.

The term “lunula” came from the Latin word “luna” and was used for round brackets in early history as the shape of the round bracket is similar to the crescent moon.

The singular for parentheses is “parenthesis” which can be referred to the right or left round bracket. The round brackets are shown in figure 2.

Figure 2 – Round Brackets

Parentheses are also used in English literature to add extra information to the text. They are also used in expressions where the singular and plural of the word are required at the same time—for example, the writer(s).

Round brackets are often nested in the innermost part of an algebraic expression. The math operator in the round brackets is performed first regardless of its precedence over the other operator with it in the square brackets.

For example, in the equation:

[ 8 ÷ ( 5 – 3 ) ] 

The division should be performed first over subtraction according to the order of operations but the round brackets overshadow this precedence.

The round bracket has the highest priority and so the answer will be 4.

Parentheses are also used to define a function in terms of its variable such as f(z) represents a function of variable z.

They are also used to define the domain and range of a function if there is any discontinuity or the graph goes up to infinity on the interval side.

Square Brackets

Square brackets are also known as closed brackets, brackets, and box brackets.

They are used in algebraic equations to enclose more terms outside the round brackets and thus have the second precedence after the parentheses. Figure 3 shows the square brackets.

Figure 3 – Square Brackets

They are also used to define an interval in graphs.

For example, in [1,9) the left square bracket suggests that 1 is included in the interval and the right parenthesis suggests that 9 is not included. 8.99 is included but 9 is not included.

Square brackets are also used to define matrices and chemical concentrations in solutions.

Curly Brackets

Curly brackets are also known as braces, flower brackets, and swirly brackets. They have the third precedence after parentheses and square brackets. They are shown in figure 4.

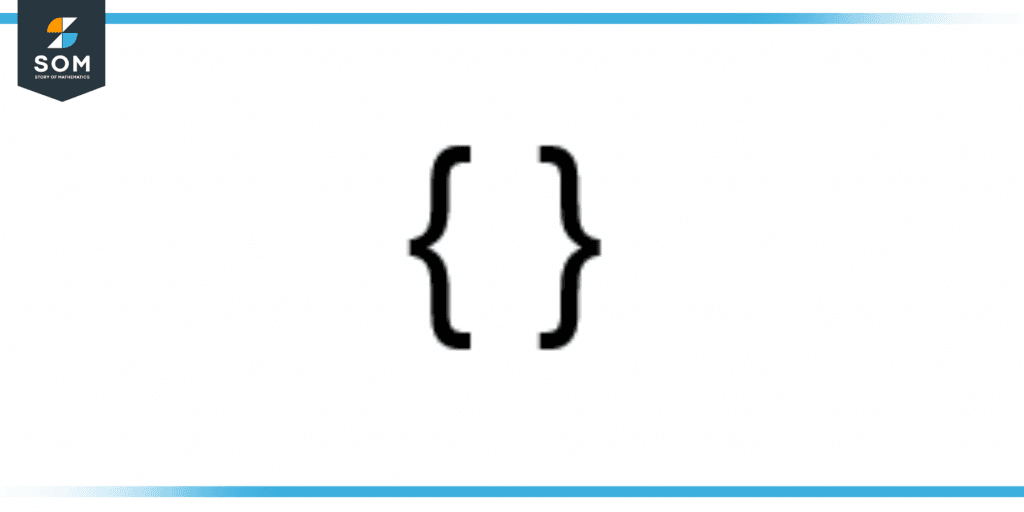
Figure 4 – Curly Brackets

Curly brackets are used in algebraic expressions and to define sets such as subsets, power sets, or supersets, etc.

Angle Brackets

Angle brackets are also known as broken brackets, pointy brackets, diamond brackets, or chevrons. The brackets are similar to the less than and greater than signs. Figure 5 shows the angle brackets.

Figure 5 – Angle Brackets

Angle brackets are used to define averages with respect to time or any other variable. They are used to identify ordered pairs.

Rules for Order of Operations

The order of operations is the set of rules that signify which mathematical operation should be carried out first while solving an algebraic expression. This order is described by the following two acronyms.

BODMAS

BODMAS stands for “Brackets Orders Division Multipliplication Addition Subtraction”. Brackets are the first to look for while solving a mathematical expression.

Orders are the powers or exponents which are calculated after brackets. After these come division and multiplication which have more precedence than addition and subtraction.

Sometimes, the acronym BIDMAS is also used for BODMAS with “I” standing for “Indices”.

PEMDAS

PEMDAS stands for “Parentheses Exponents Multiplication Division Addition Subtraction”. It is the same order of operation as BIDMAS or BODMAS. The multiplication and division and the addition and subtraction are checked from left to right.

Order of Brackets In Solving Algebraic Expressions

Brackets are analyzed first and foremost while solving an algebraic expression. The terms in the interior-most bracket which is usually the parentheses are solved first regardless of the mathematical operation in it.

The next bracket to solve according to the PEMDAS rule is the square bracket and the last to solve is the curly bracket.

Although all brackets serve the same purpose of enclosing various terms, this order can be flexible. But most commonly, the parenthesis is used in the inner-most part of the expression and first solved.

Also, the bar or vinculum is solved even before the round brackets as they are usually enclosed in the parentheses if they involve three or more math operations.

So conclusively, brackets have the top priority in solving algebraic equations.

Solving an Expression With the PEMDAS Rule

Solve the algebraic expression given below:

5x – { 3y – [ 4x – ( 5y – 6x – 7y ) ] }

Solution

According to the PEMDAS rule, the parentheses are solved first. In the round brackets, 5y and 7y are like terms so they can be subtracted. Like terms have the same variable and power on the variable.

So, the equation becomes:

5x – { 3y – [ 4x – ( 5y – 7y – 6x  ) ] }

5x – { 3y – [ 4x – ( – 2y – 6x  ) ] }

The parentheses are not removed as the minus sign outside the parentheses will change the signs of terms inside the round brackets. So, further solving gives:

5x – { 3y – [ 4x + 2y + 6x ] }

Solving the square bracket and adding the like terms 4x and 6x gives:

5x – { 3y – [ 10x + 2y ] }

5x – { 3y – 10x – 2y }

Solving the braces gives:

5x – { y – 10x }

5x – y + 10x

So, the final answer is:

15x – y

All the images are created using GeoGebra.

Box And Whisker Plot Definition < Glossary Index > Byte Definition