Convert|Definition & Meaning

Why is Conversion Required?

It is necessary to convert the units to find solutions to many of the mathematical issues. To make the necessary computations, converting between different mathematical units is required. To find the area of a triangle in centimeters, for instance, if the base is given in centimeters and the height is supplied in meters, but the question asks you to find the area of the triangle in centimeters, you will need to convert the height from meters to centimeters. Therefore, one must have a working knowledge of the various unit conversions to convert one unit into the desired unit.

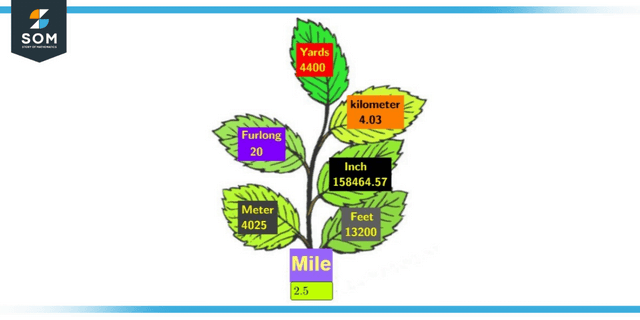
Figure 1: Distance (Mile) Conversion

Unit Conversion

A different unit of measurement can be expressed with the same property through a unit conversion. For example, time can be represented in minutes rather than hours, and miles can be converted to kilometers, feet, or any other unit of length measurement. Likewise, distance can be represented in any unit of length measurement. Measurements are frequently provided with a set of units, like feet, even when the information must also be available in another set of units, such as chains. A conversion factor is a numerical equation that allows one unit of measurement, such as feet or chains, to be converted into another with the same value.

Conversion Factor

A conversion factor is a number that can be multiplied or divided to shift the units of measurement used for one set to another. When a conversion is required, the correct conversion factor that results in the same value must be utilized. To convert inches to feet, for instance, the correct value for the conversion is 12 inches equaling 1 foot. The correct ratio of converting minutes to hours is sixty minutes to one hour, which means that one hour is equivalent to sixty minutes.

Examples of Conversion Factors

The most common types of measurements that need to be converted are length (linear), area (two-dimensional), and volume (three-dimensional). Still, you can also use conversion factors to convert things like mass, speed, density, and force. Many different kinds of measurements sometimes need to be converted. The imperial system (feet, pounds, and gallons), the International System of Units (SI, and the contemporary form of the metric system: meters, kilograms, and liters), and the conversions between the two need the employment of conversion factors.

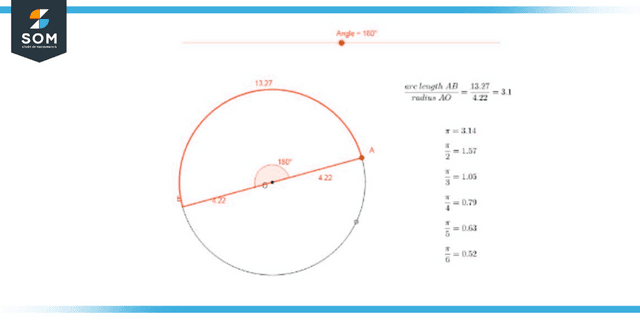
Figure 2: Degree to Radian Conversion

It is essential to remember that the two values need to indicate the same quantity. For instance, converting between two different mass units (such as going from grams to pounds) is possible. Still, it is typically impossible to convert between different volume and mass units (e.g., grams to gallons).

Conversion Table

Using previously established units, conversion factors, and the knowledge that a unit of measure that is equal to itself cancels out that unit is the component that goes into constructing a unit cancellation table. The table is constructed so that all of the units, except for the one sought, cancel out. For a unit to be cancelled, it must appear both in the numerator and in the fraction’s denominator. When you multiply across the table, the number at the top will be divided by the number at the bottom, and the answer you get will be in the units you choose.

Unit Conversion in Field

Converting units of measurement out in the field requires that you have experience doing it. Writing down your unit cancellation table on a piece of paper, the back of a wrapper, or anywhere else that might be handy will ensure that you preserve the units in the correct order. It is essential to effective planning to solve problems in units that are already familiar to the fire staff. The consequences of getting the unit wrong might be rather severe.

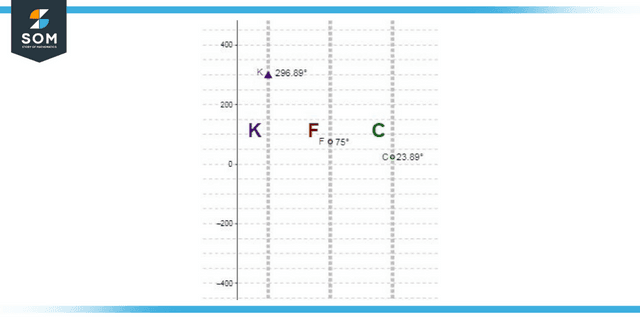
Figure 3: Temperature Conversion

Check the accuracy of your result by applying what you understand about units. You are aware that one foot does not equal a chain. The conversion from feet to chains should give you a smaller number since the ultimate result will be in chains, and each chain has several feet. This happens because the outcome will be in chains.

Importance of Mathematical Conversions

We need to convert one measurement unit to another to achieve precision in our measurements and avoid misunderstandings. To give just one illustration, the length of a pencil is not typically measured in kilometers. In such a circumstance, one must convert from kilometers (km) to centimeters (cm). In most cases, multiplicative conversion factors are used to convert from one unit of measurement of a given amount to another unit of measurement of the same quantity. Let’s look at how to convert one length unit into another and one mass unit.

Examples of Unit Conversions

Example 1

A prescription of 12mg dosage was described to a man who is allowed to get two refills with the given prescription. For instance, 60 tablets are prescribed to the patient, and 4mg of drug is in every tablet, find the dosages in the three prescriptions (Two Refills and Original)?

Solution

Three Prescriptions = Three Prescriptions x [(60 Tablets) / (1 Pres.)] x [(4mg) / (1 tablet)] x [(1 dosage) / (12mg)]

Cancel all the units that are in common within the numerator and denominator.

= (3 x 60 x 4 x 1) / (1 x 1 x 12)

= 720 / 12 Dosages or Sixty Daily Dosages.

Example 2

The human heart beats approximately 70 times a minute on average. Find the total number of heart beats for an average human in a year?

Solution

There are 365 days in a year and each day has 12 hours.

Total Hours in 365 days are: 365 x 12 = 4,380 hours.

Now, there are sixty minutes in each hour, so in a year, there will be 4,380 x 60 = 262,800 minutes.

The human heart beats 70 times a minute; therefore, the total beats become 262,800 x 70 = 18,396,000 beats.

All mathematical drawings and images were created with GeoGebra.