JUMP TO TOPIC
Denominator|Definition & Meaning
Definition
In a fraction, the number under the horizontal line is called the denominator. The denominator of a fraction indicates how many identical subparts make up the whole.
What Is the Denominator?
The component of a fraction that falls below the fractional bar is referred to as the denominator. The total number of components that comprise the whole can be found in the denominator.
A bar is horizontally placed between two integers; sometimes, the symbol “/” can be used to identify a fraction. The name “fractional bar” refers to this bar or this symbol. The number displayed on top is referred to as the “numerator,” while the number displayed below the fractional bar is referred to as the “denominator.”
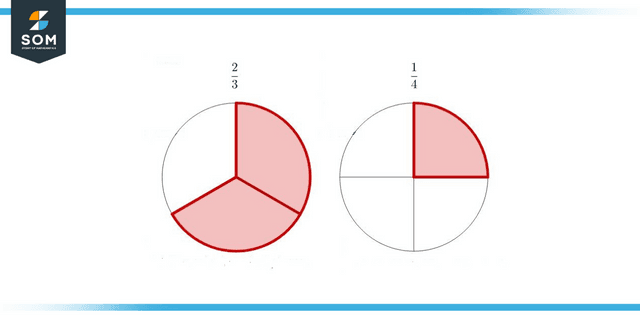
Figure 1: Representation of Different Denominators
In any fraction written as (a / b), the letter a represents the numerator, and the letter b represents the denominator. A fraction denotes a portion of the whole. It can be demonstrated using mathematics by dividing two numbers together. For instance, one quarter is one part of the four equal parts generated when one thing is divided into four parts. The numerator for this fraction is 1, and the denominator is 4.
Denominator and Numerator
The denominator indicates the number of components that comprise a unit or a whole thing. The numerator indicates the number of components chosen from the total number of equivalent parts. For instance, in fraction (3 / 5), numerator 3 refers to the three equal portions we chose, while denominator 5 refers to the five equal parts that were initially formed. The whole is composed of five equal components.
Least Common Denominator
When the denominators of two or many fractions are identical, we refer to those denominators as common denominators. The term “least common denominator” refers to the lowest number that can serve as a common denominator for a particular group of fractions. The only way to perform operations such as adding and subtracting fractions or considering alternative or more fractions is if the fractions in question share a common denominator. Consider the following scenario: we now have to add (3 / 8) and (1 / 8). Because the denominators are precisely the same, they may be added together as though they were fractions, and the conclusion will be (3 / 8) + (1 / 8), equaling (4 / 8), which is the same as (1 / 2).
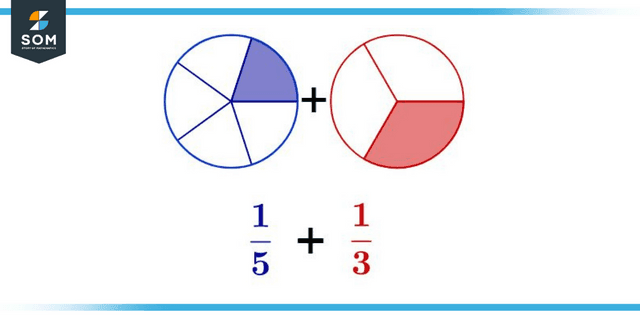
Figure 2: Addition of Fractions
Similar fractions are those that have the same numerator in their fractional breakdown. Take, for instance, the numbers 5/15, 3/15, 17/15, and 31/15. The fractions that have different denominators from one another are referred to as, unlike fractions. Take, for instance, the numbers (2 / 7), (9 / 11), (3 / 13), and (39 / 46).
We need to change the given fractions into equivalent fractions with the same denominator to convert the unlike fractions that have been given to like fractions because the denominators are different. It is possible to accomplish this by locating the Least Common Multiple (LCM) of the denominators, also called LCD (Least Common Denominator).
Things To Remember
- A denominator must be an integer.
- A denominator can never equal zero since there are never precisely zero elements that make up an entire thing.
- The ideas of rational numbers, ratios, and proportions, and division all make extensive use of the term “denominator.”
How To Find Unknown Denominator
In a fraction in which either the numerator or the denominator is unknown, you must cross-multiply the fraction’s numerators and denominators to solve the problem. To perform a cross-multiplication, all that is required is to multiply each numerator by the denominator that appears in the corresponding opposite fraction. You will be given a different equation to deal with; as a result, one that does not involve any fractions.
How exactly does one use cross multiplication to determine the denominator in an unknown situation? An ‘X’ will be used to denote a denominator that is unknown while working with algebraic equations.
Figure 3: Subtraction of Fraction with Same Denominator
Step 1
The first thing to do is to cross-multiply the fractions, as was covered in the previous section. This will result in a brand-new equation that can be solved with significantly less effort.
Step 2
After completing the cross-multiplication of your fractions, the equation you have just produced needs to be solved. Firstly, you have to obtain “X” on its own.
Step 3
The final phase in this process involves decreasing the fraction. Finding the most significant common factor between the numerator and the denominator is the first step in accomplishing this task.
If the fraction’s numerator is more than one, it is recommended to be converted into a mixed number. To accomplish this, you need only divide the numerator by the denominator in your calculations. Following this step, you will be left with a whole number and a fraction. The original denominator will serve as the numerator, and the remainder will be the denominator.
Solved Examples of Expressions Involving Denominators
Example 1
What is the solution of the following numerical?
(2 / 3) + (2 / 6)
Solution
Since the denominators of both fractions are different, we’ll take LCM.
3 = 3
6 = 2 x 3
The least common factor is three and two; therefore, the LCM becomes 3 x 2 = 6
(2 / 3) + (2 / 6) = [(2 + 2) / 6]
= (4 / 6) or (2 / 3)
Example 2
What is the solution to the following numerical?
(2 / 4) + (2 / 8) + (2 / 12) + (2 / 14)
Solution
Again, the denominators of both fractions are different; we’ll take LCM.
4 = 2 x 2
8 = 2 x 2 x 2
12 = 2 x 2 x 3
14 = 2 x 7
The least common factor is two, two, two, and two; therefore, the LCM becomes 2 x 2 x 2 x 2= 16:
(2 / 4) + (2 / 8) + (2 / 12) + (2 / 14)
= [(2 + 2 + 2 + 2) / 16]
= (8 / 16)
= (1 / 2)
All mathematical drawings and images were created with GeoGebra.
