Divisible|Definition & Meaning

What Is Meant by Divisible?

A number is said to be divisible if it is entirely divided by any other number without leaving a remainder. When we say that a certain number is completely divisible by another number, it means that a quotient is a whole number, and there is no remainder left.

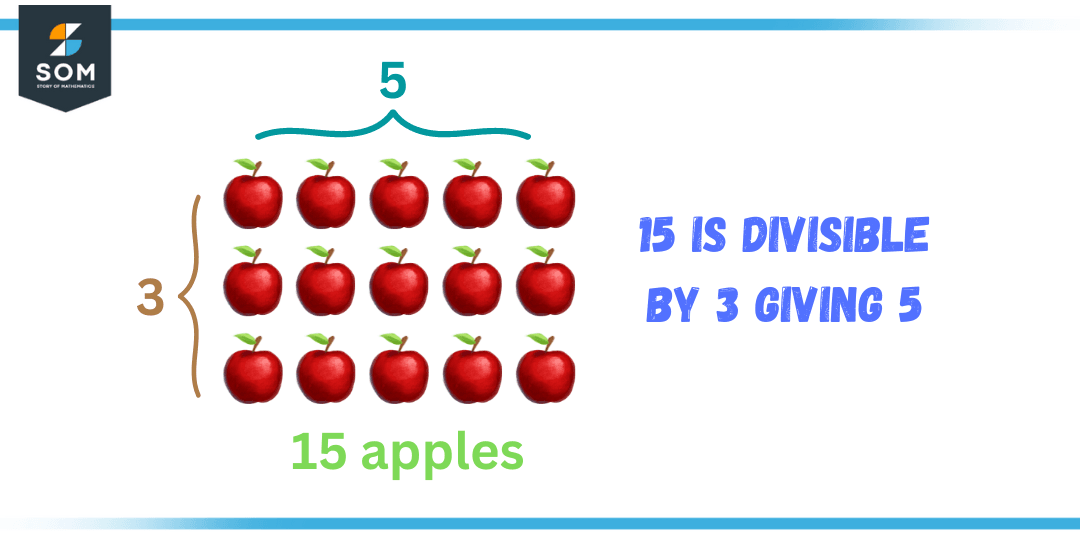
Figure 1 – 15 is divisible by 3 which gives 5

If we want to know the factors of a particular number, divisibility plays an important role in it. For example, 2,3,4, and 6 are the factors of 12 because all of these divide 12 completely, giving zero remainders.

Some of the methods to find the divisibility of a number are by using divisibility rules, prime factorization, and greatest common divisor (GCD).

Prime Factorization

One of the methods for determining divisibility is by using prime factorization.  If a number is the factor of the prime factorization of a particular number, then that particular number is divisible by it. For example, take the number 35; we know that 5*7=35, so 5 and 7 are the prime factors of 35 and hence 35 is divisible by 5 and 7.

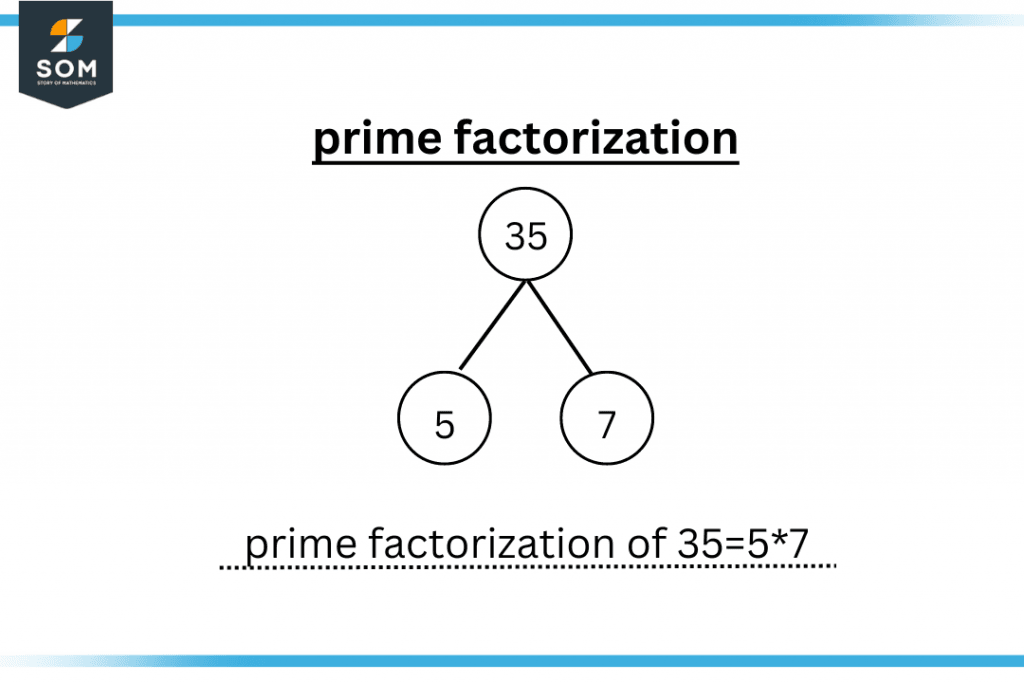
Figure 2 – Prime factorization of 35

Divisibility Rule

To review whether a particular number is completely divisible by 2 or not, we have to look at the last number of the given numerical value. If a number is even or it ends with 0,2,4,6 or 8, then it is completely divisible by 2.

Divisibility Rule of 1

We know that every number is completely divided by 1, leaving no remainder. No matter how large the number is, dividing it by 1 will yield the number itself as a quotient. For example,12876 is divisible by 1. So there is no specific condition for any number divided by 1.

Divisibility Rule of 2

To review whether a particular number is completely divisible by 2 or not, we have to look at the last number of the given numerical value. If a number is even or it ends with 0,2,4,6 or 8, then it is completely divisible by 2.

For example, 3256 is divisible by 2 because it ends with an even number, but if we consider the number 3257, whose last digit is 7, thus not being an even number hence 3257 is not divisible by 2.

Divisibility Rule of 3

There is an easy method to figure out if an integer is dividable by 3. For divisibility by 3, we have to add all the numbers of the given numerical value. If the sum gives a number that is completely divided by 3, then the number as a whole is divisible by 3.

Suppose the numerical value is 35682; add all the numbers of this value 3+5+6+8+2. The answer to this addition is 24, which is completely divisible by 3 so 35682 is also divisible by 3. On the contrary, 35681 is not divisible by 3 because its sum is 23, which is not divisible by 3.

Divisibility Rule of 4

The Divisibility rule of 4 is that if the last two digits of any numerical value are divisible by 4 and give zero remainders, then the number as a whole is divided by 4.

Let us consider the numerical value 7512; the last two digits, 12, are divisible by 4, 12/4=3, so 7512 is divisible by 4. But 7502 is not completely divisible by 4 because 4 is not a factor of the last two digits.

Divisibility Rule of 5

The divisibility rule of 5 is very simple and easy to practice. The only numbers divisible by 5 are the ones whose ending value is either a zero or 5.

For example, 43265 is divisible by 5 because it ends with 5, but 43266 is not divisible by 5 due to the ending number, i.e., 6.

Divisibility Rule of 6

A number is completely divisible by 6, leaving zero remainder when it is a factor of both 2 and 3. In other words, we can say that if a number ends with even values and the summation of all of its values is a factor of 3, then the number as a whole is divided by 6.

For example, 540 is divisible by 6 as it ends with an even number(hence 2 is a factor), and adding its number gives 9, which is divisible by 3 (hence 540 is divisible by 3).

Divisibility Rule of 7

The divisibility rule of 7 is a bit complicated as compared to other numbers’ divisibility. Let us understand this by using an example.

Suppose a value of 14497; first, we have to multiply the last number, i.e., 7, by 2, which gives 14. Now subtract 14 from the remaining number, i.e., 1449, which gives 1435. If 1435 is divisible by 7, then 14497 is also divisible by 7.

If again you want to check the divisibility of 1435, repeat the process by multiplying 5 by 2 and deducting it from the remaining value, which gives 133, which is easily divisible by 7. Hence 7 is a factor of the number 14497.

Divisibility Rule of 8

An integer is completely divisible by 8 if and only if the leftmost three values of that number are divided by 8, leaving zero remainders. For instance, 35408 is a number, and its last three digits, i.e., 408, are divided by 8 completely, so the number as a whole is divisible by 8.

Divisibility Rule of 9

The rule for divisibility by 9 is identical to the rule for divisibility by 3. Let us understand it by an example. 23454 is a numerical value that we want to check. The sum of its digits is 18, and 9 is a factor of 18, so 9 is also a factor of 23454.

Divisibility Rule of 10

Any number that ends at zero is divisible by 10. For suppose 25430 and 4950 are divisible by 10, but 495 and 2543 are not completely divisible by 10.

Divisibility Rule of 11

For an integer to be completely dividable by 11, we have to follow a few steps.

• Observe the number carefully.
• Add the digits alternatively.
• Subtract both the sums obtained in the above step.
• If the difference is zero or a number that is multiple of 11, then the number as a whole is divisible by 11.

Let’s apply these steps to an example. Consider the number 723954. Adding the alternate numbers, i.e., 7+3+5 and 2+9+4. The sums are 15 and 15. Subtracting both sums produces zero, which satisfies the condition for divisibility by 11. Hence the number 723954 is divisible by 11.

Greatest Common Divisors (GCD)

Divisibility can also be determined by using the Euclidean algorithm. It is a method to locate the GCD of two numbers. We know that GCD gives out the largest number providing no remainder when dividing both numbers.

For example, the GCD of 12 and 8 is 4, which means that 4 is the largest number that divides both 12 and 8 without leaving a remainder. So 12 and 8 both are divisible by 4.

Figure 3 – This is how the greatest common divisor is calculated

Solved Examples of Divisibility of a Number

Example 1

Check whether 23487 is divisible by 3 or not.

Solution

The first step of the divisibility rule of 3 is adding all the values.

2+3+4+8+7=24

Since 24 is divisible by 3, so the number 23487 is also divisible by 3.

Example 2

Check whether 93456 is divisible by 5 or 7.

Solution

The number 93456 is not divisible by 5 because its ending number is neither 5 nor 0.

To check divisibility by 7, we have to follow the steps of the divisibility rule of 7.

Multiplying the last digit by 2, 6*2=12.

Now subtract 12 from the rest of the number, i.e., 9345.

9345-12=9333

To check that 9333 is divisible by 7, repeat the process.

The last digit, 3, multiplied by 2, gives 6.

Subtract 6 from 933, which gives 927.

927 is divisible by 7, so 9333 is divisible by 7, and hence the number 93456 is also divisible by 7.

All images are created using GeoGebra.