JUMP TO TOPIC
Extraneous Root|Definition & Meaning
Definition
An extraneous root is a value reached for a variable in answer to a problem that is not an actual root of the equation. When you are solving a system of algebraic equations and come up with more than one solution (or multiple roots), some of those roots may not satisfy the equations. These are called extraneous roots!
It is essential to double-check each root by reinserting it into the mathematical system.
The root is referred to as an extraneous root. It should be removed from the solution set if it fails to satisfy the system or fulfill other requirements like the root has to be favorable, the root cannot equal 1, or the root should be a real integer.
Figure 1 below shows the extraneous root of (=4 and -4).
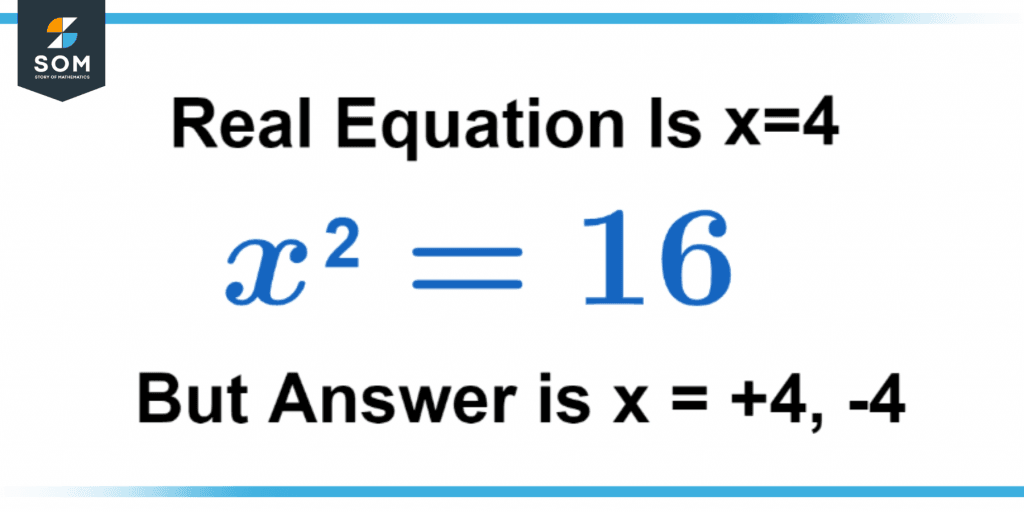
Figure 1 – Representation of extraneous root.
Why Do Extraneous Solutions Occur?
Extraneous Solutions appear because there are two solutions when you square the two sides of a square root problem. As a result, one of those figures will represent an additional solution or a solution that is added but does not satisfy the initial equation.
Only when arithmetic is used to describe and solve an issue in the actual world is it rooted unnecessarily. A straightforward mathematical model might only sometimes accurately reflect reality.
The model’s solutions are only sometimes practical and may not even be what is desired. By adding all known restrictions to the issue, unnecessary solutions may have been avoided in many instances. For instance, according to the angle of release, the arrow’s range launched with a specific beginning speed can take on various values.
The other alternatives are no longer viable if the maximum distance is what we are after.
The definition given above is flawed, however, in that it omits the qualifier by “correct or proper method.”
The procedures that are often considered to be correct include:
- Adding like amounts together.
A double is created by adding a number twice. Therefore, we say that a number has been doubled if we multiply it by two or add it to itself. Double numbers denote twice the specified quantity or number. - Delete the same values.
Subtract the identical quantities from both sides to equalize the equation. - Multiplying the same quantity is required.
The results are also identical when multiplied by the extra equals.
Figure 2 and Figure 3 below shows the square of a value may be calculated by multiplying & adding the same set of integers.
Figure 2 – Representation of square of integers.
Figure 3 – Representing addition of integers.
- Dividing by equals and multiplying equal by equals are also options.
When equals are divided among themselves, the quotients are also equal. - Extraction of equal roots from equals.
Find equal roots from the same numbers on both sides of the equation.
Extracting Square Roots as Extraneous Roots
Square Root Property
The Square Root Rule is utilized to solve quadratic equations by removing the square exponent to focus on the variable being solved. The negative and positive numbers that may be multiplied by themselves to equal x are provided by the formula x=$\mathsf{\sqrt{a}}$, x = +a, -a.
Extracting Roots
The square is isolated when extracting roots, and the square root quality is used. The square root ability is used to create two mathematical equations that can individually be solved. Make sure to rationalize the denominator if required and simplify all radical expressions.
Remember that if a quadratic equation equals 0, it is in standard form:
ax$\mathsf{^2}$ + bx + c = 0
Standard Form
Standard form is Any value within 1.0 and 10.0 that can be expressed as just a decimal number and is multiplied by a power of 10.
Where a≠0 and the real numbers a, b, and c are present, a root of a quadratic function denoted by is a solution to an equation. There can be two real solutions to a quadratic equation, one real answer, or none at all—in which case; it will result in two complex answers. We may use factoring to solve the equation if the quadratic expression divides.
Quadratic Polynomial Expression
A quadratic expression is a polynomial of degree two in one or more variables. A quadratic polynomial defines the form known as just a quadratic equation. The graph for a quadratic function has the form of a parabola. Although a parabola’s “width” or “steepness,” as well as its opening direction, might change, they all have the same basic “U” shape.
Parabola
A parabola is a mirror-symmetrical, roughly U-shaped planar curve. The same curves can be defined by various irrelevant mathematical definitions that correspond to them. A spot, as well as a line, can be used to depict a parabola.
Complete Squares in Extraneous Roots
Solving the equation, which entails modifying the equation’s form so that the left side resembles a perfect square, is used to solve quadratic equations.
(x – y)$\mathsf{^2}$ = z
Consider the equation x$\mathsf{^2}$ + 8x + 20 = 8 as an illustration. This equation’s square must first be completed by subtracting 4 from both sides. It comes out to x$\mathsf{^2}$ + 8x + 20 – 4 = 8 – 4. We now get the square roots of the equation, x$\mathsf{^2}$ + 8x + 16 = 4, on both sides. There is a solution to the problem x + 4$\mathsf{^2}$ = 2$\mathsf{^2}$.
How To Know Whether Equation Is Extraneous or Not?
An equation’s solution appears to be correct but is later found to be incorrect by replacing it with the original equation.
As an illustration, consider the equation “x” and “y,” which has two roots (in which it remains unchanged).
The original equation becomes zero when you add “x,” but it doesn’t when you add “y.”
Thus, “y” is an extra root. When we square all sides throughout our solution, this frequently occurs.
Solved Example of Extraneous Root
For x, solve the equation $\mathsf{\sqrt{x+9}}$ = x – 3
Solution
Squaring both sides to eliminate the square on the left side:
$\mathsf{\left(\sqrt{x+9}\right)^{2}}$ = (x – 3)$\mathsf{^2}$
Now, we have:
x + 9 = x$\mathsf{^2}$ – 6x + 9
With the equation rearranged, we obtain the following:
x$\mathsf{^2}$ + 6x + 9 – x – 9 = 0
x$\mathsf{^2}$ – 5x = 0
Taking x common, we have:
x(x – 5) = 0
We now have 2 answers for x: x = 5 and x = 0. Before we finalize, we need to check the results for validity.
First Root: x = 5
Firstly putting x = 5 in the equation $\mathsf{\sqrt{x+9}}$ = x – 3. We get:
$\mathsf{\sqrt{5+9}}$ = 5 – 3
$ \mathsf{ \sqrt{14}}$ = 2
We know the square root of 14 does not equal 2, so x = -5 is an extraneous solution.
Second Root: x = 0
Now putting x=0 in the equation $\mathsf{\sqrt{x+9}}$=x – 3. We get:
$\mathsf{\sqrt{0+9}}$ = 0 – 3
$\mathsf{\sqrt{9}}$ = -3
We get 3 = 3, which is valid. Therefore, x = 0 is a solution.
All images are created using GeoGebra.
