Factorising|Definition & Meaning

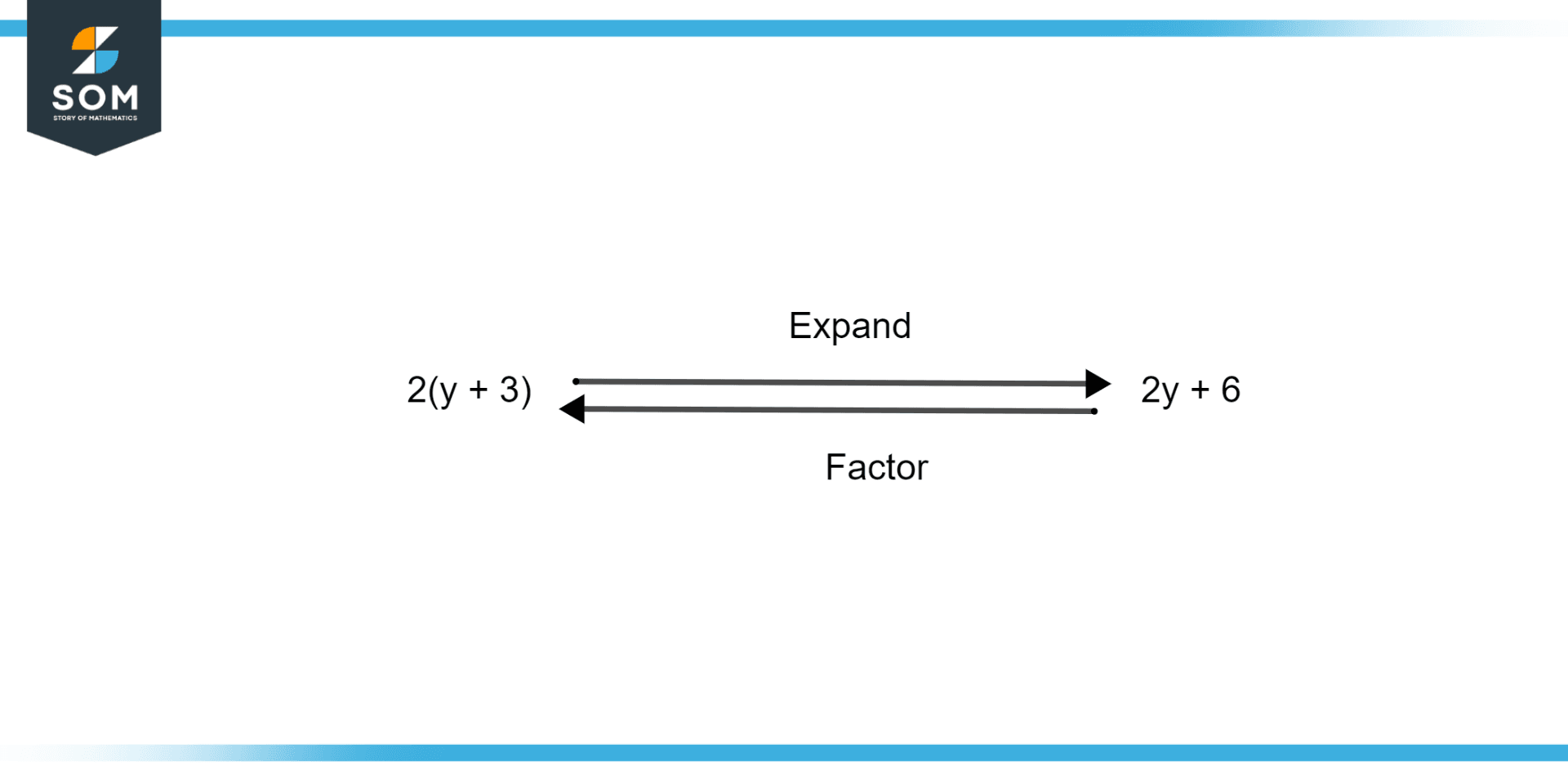
Figure 1 – Difference Between Expansion and Factors 

Figure 1 illustrates the difference between factors and the expansion of an equation.

Greek mathematicians were the first to think about factorization in the context of integers. They established the arithmetic basic theorem, which states that any positive integer can be factored into a product of prime numbers but that no prime number can be factored into an integer larger than one.

Furthermore, this factorization is exclusive to the factor order. Even though integer factorization is somewhat of the opposite of multiplication from an algorithmic perspective, the RSA cryptosystem uses this fact to construct public-key cryptography.

Factorization, also known as factoring, is the mathematical process of breaking down an item (such as a number, a matrix, or a polynomial) into the product of one or more additional entities, or factors, whose multiplication yields the original number, matrix, etc. The majority of this concept will be covered in your lower secondary courses, which include grades 6 through 8.

An integer or polynomial is simply divided into parts that, when multiplied together, yield the original or starting integer or polynomial. Any algebraic or quadratic equation may be made simpler using the factorization technique by expressing the equations as the product of factors rather than by expanding the brackets.

An algebraic expression, a variable, or an integer can all be parts of an equation.

For millennia, people have also researched polynomial factorization. Finding a polynomial’s roots in elementary algebra is simplified to finding the roots of the components by factoring the polynomial.

The irreducible polynomial property, a variant of the basic theorem of arithmetic using irreducible polynomials in place of prime numbers, is a property that applies to polynomials with coefficients in the integers or in a field.

Particularly, a univariate polynomial with complex coefficients permits a singular (up to ordering) factorization into linear polynomials; this is a variant of the algebraic basic theorem.

Root-finding methods can be used in this situation to factorize the data. Computer algebra starts with the case of polynomials with integer coefficients.

A unique factorization domain is a commutative ring with a unique factorization characteristic. There are number systems that do not have a single factorization domain, such as some rings of algebraic integers. Rings of algebraic integers, however, meet the Dedekind domains’ weaker condition, which states that ideals factor only once into prime ideals.

Factorization can also refer to more broad breakdowns of a mathematical entity into its component parts, which are smaller or simpler. For instance, each function might be included in the mix of an injective function and a surjective function.

There are several matrix factorizations that may be applied to matrices. In the matrix formulation of Gaussian elimination, each matrix, for instance, has a distinct LUP factorization, which is the product of a lower triangular matrix L with all diagonal entries equal to one, an upper triangular matrix U, and a permutation matrix P.

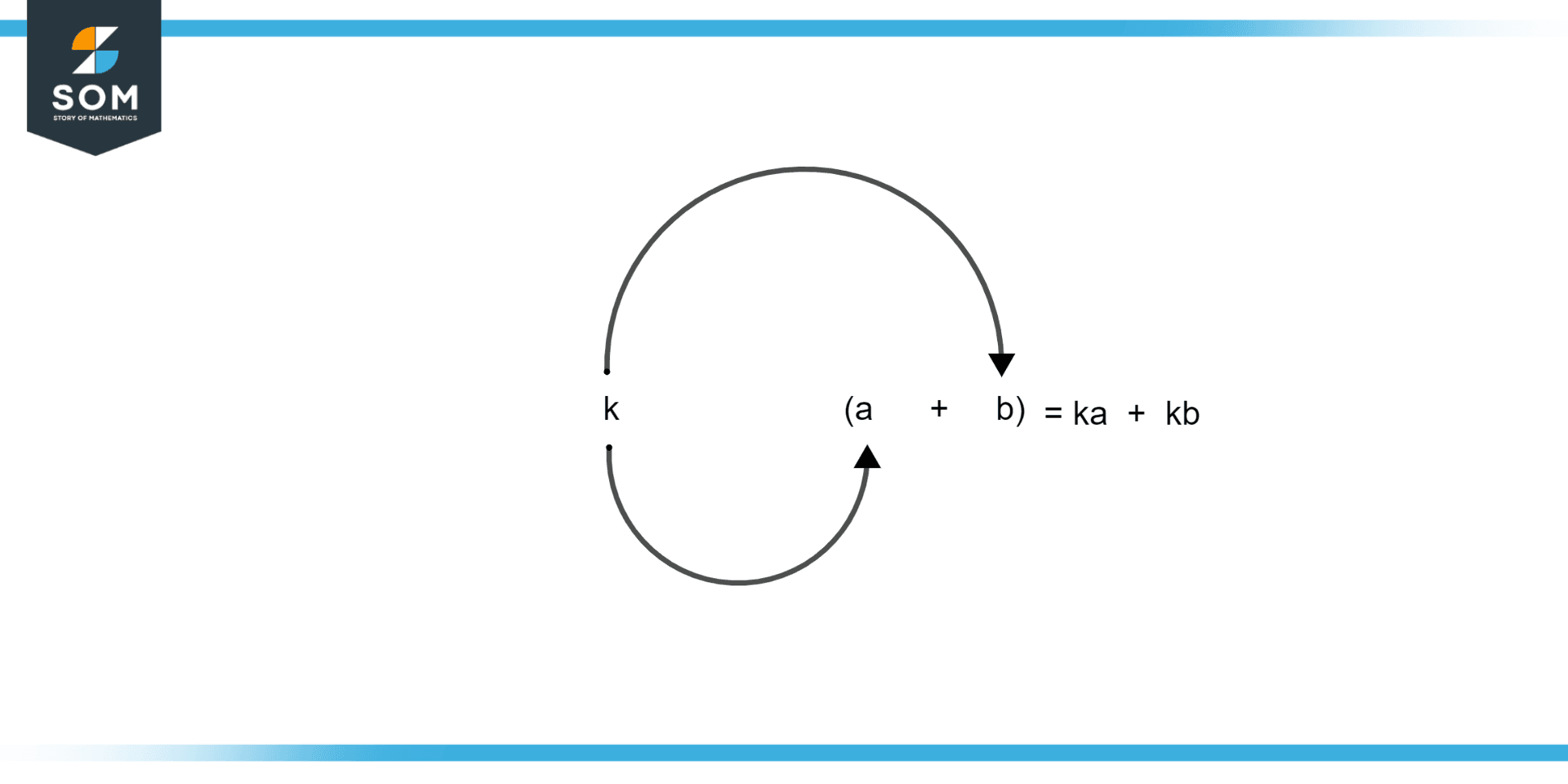
Figure 2 – Factorization of an Expression

Figure 2 illustrates the Factorisation of an Expression.

Factorisation in Algebra

The division of 12 by the integers 1, 2, 6, and 12 leaves no residue, making them all factors of 12. It is a crucial algebraic procedure that is used to solve equations, simplify fractions, and simplify expressions. Factorisation in algebra is another name for it.

Difference Between Terms and Factors

It is anything that has to be added or removed from an expression (subtracting involves adding a negative value). 2x and 7 are the terms if 2x + 7 is an expression. Where sum equals terms plus terms.

In an expression, it is anything that has to be multiplied. Where a product is equal to a factor multiplied by a factor. For instance: p = 4(2q – 6).

Basic Formula for Factorisation

The basic formulae for factorisation are:

• (a + b)², which is equal to a² + b² + 2ab
• (a – b)², which is equal to a² + b² – 2ab
• a² – b², which is equal to (a + b) (a – b)
• a³ – b³, which is equal to (a + b)(a² + ab + b²)
• a³ + b³, which is equal to (a + b)(a² – ab + b²)

Factorisation Methods

Following are the four methods to factorize an algebraic expression.

• Method 1: Common factors method
• Method 2: Regrouping terms method
• Method 3: Factorisation using identities
• Method 4: Factors of the form (x + a)(x + b)

Method 1

With this approach, we only eliminate the elements that each phrase in the provided statement has in common.

Method 2

Regrouping entails reorganizing the provided statement using words that are related or identical to one another.

Method 3

By using the basic formula of factorization.

Method 4

The factors of an expression will be (x+a) and (x + b) if it takes the form x² + (a + b) x + ab.

Factorisation for a Quadratic Polynomial

A polynomial called a “quadratic” is expressed as “ax² + bx + c,” where “a,” “b,” and “c” are simple integers. You may get the two integers that will multiply to equal the constant term “c” and add up to equal “b,” the coefficient on the x-term, in a simple instance of factoring.

It’s crucial to factorize algebraic formulae while solving quadratic polynomials. In most circumstances, such as with fractional formulae, factorization may be used to condense a formula instead of removing all the brackets when decreasing it.

Some Examples of Factorisation

Example 1

Factorize the following Quadratic Polynomials:

a) x² + 7x + 6

b) x² + 7x + 12

c) x² + 3x + 2

Solution

a) The constant term in the quadratic polynomial is 6, which can be written in the product form of 2 and 3 or 6 and 1. We need to have 7, and 6+1 is equal to 7, so the equation can be written in the form of:

x² + 7x + 6

x² + 6x + x + 6

For the factorization, we can have x and 1 common from the equation

x(x + 6) + 1(x + 6)

(x + 1)(x + 6)

So the (x + 1) and (x + 6) are the factors of the polynomial x² + 7x + 6.

b) The constant term in the quadratic polynomial is 12, which can be written in the product form of 4 and 3 or 6 and 2. We need to have 7, and 4+3 is equal to 7, so the equation can be written in the form of:

x² + 7x + 12

x² + 4x + 3x + 12

For the factorization, we can have x and 3 common from the equation:

x(x + 4) + 3(x + 4)

(x + 4)(x + 3)

So the (x + 4) and (x + 3) are the factors of the polynomial x² + 7x + 12.

c) The constant term in the quadratic polynomial is 2, which can be written in the product form of 2 and 1. We need to have 3, and 2+1 is equal to 3, so the equation can be written in the form of:

x² + 3x + 2

x² + 2x + x + 2

For the factorization, we can have x and 1 common from the equation:

x(x + 2) + 1(x + 2)

(x + 1)(x + 2)

So the (x + 1) and (x + 2) are the factors of the polynomial x² + 3x + 2.

Example 2

Factorize x² – 64 using the basic formula of factorization.

Solution

We can factorize this expression using Basic Formula for Factorisation as illustrated in figure 3:

Figure 3 – Factorization algebraic expressions using known formulae

Thus:

x² – 64 = x² – 8² = (x + 8)(x – 8)

All images were created using GeoGebra.

Factoring Definition < Glossary Index > Fahrenheit Definition