JUMP TO TOPIC
Finite Number|Definition & Meaning
Definition
A finite number is a calculable integer representing elements from a finite collection of things. It may be some natural or whole number, such as 0.
All finite numbers are well-defined and can both be used in and result from a computation.
They can be measured or quantified, unlike the undefined infinity.
Figure 1 below shows, from 1 to 10, a set of infinite numbers.

Figure 1 – Representation of a finite set using a Venn diagram.
Finite Sets
Sets with a bounded number of members are referred to as finite sets. Due to their ability to be numbered, finite sets also are known as countable sets. If the members of the items of this set are finite, then the operation would run out of items to list.
A = {0, 3, 6, 9, …, 99}
B = {a, where an is an integer between 1 and 10}
Both sets are finite because both of them are countable.
Finite Set Cardinality
The finite set’s cardinality is n(X) = an if “a” denotes the number of members in set A. A finite set has a natural number as its cardinality, or it might be zero.
Because there are 26 components (alphabets), set A comprising all English alphabets has a cardinality of 26.
As a result, n(X) = 26.
Similar to the month in a year, a collection of those will have several clusters of 12.
The elements of any finite set can then be listed in the Roster form or with curly braces.
Roster Form
A roster set is a straightforward mathematical expression of the set. The set’s components (or members) are given in a row within the curly brackets in the roster form. If the set comprises more than one element, a comma is used in a roster notation to indicate the separation of every two elements. Since each person is counted separately, the roster form is indeed known as an enumeration notation.
Figure 2 below shows the rooster for three sets.
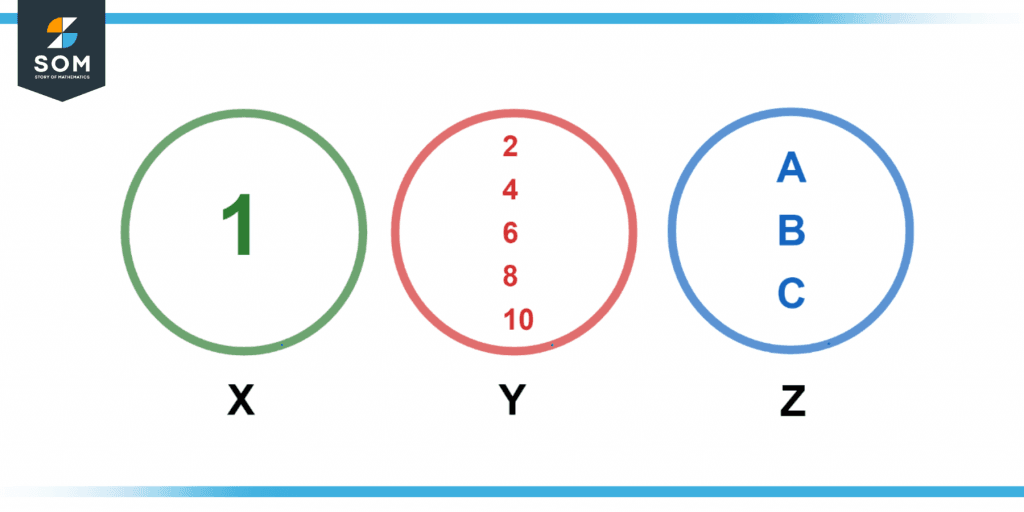
Figure 2 – Representation of roster set.
Set X only has one element. The items in roster form may be expressed using curly brackets, such as X = {1}.
Set Y comprises numerous components; hence the roster form of the elements is Y = {2, 4, 6, 8, 10}.
The components of set Z are denoted as Z = {a, b, and c}.
Properties of Finite Sets
The criteria in the preceding finite set are always valid.
- The Finite Set’s Subset
If n = 2, $\frac{Z}{a}= \varnothing$ is a finite number. The limit of f to $\mathsf{{k \ \boldsymbol\in \ N:k\leq n-2}}$ produces a bijection into $\frac{Z}{a}$ if n > 2. Thus, $\frac{Z}{a}$ is finite and consists of n – 2 components. As a result, we know its subsets ($\varnothing$ and Z) are finite if n = 2. - Two Finite Sets’ Union
In reality, the term “union of sets” refers to the intersection of two or more sets. All the items included by the united sets are in a union of two or more sets. Because the sets being joined are finite sets, it makes sense that combining two or even more finite sets would always result in a finite set.
Figure 3 below shows the union of two sets.
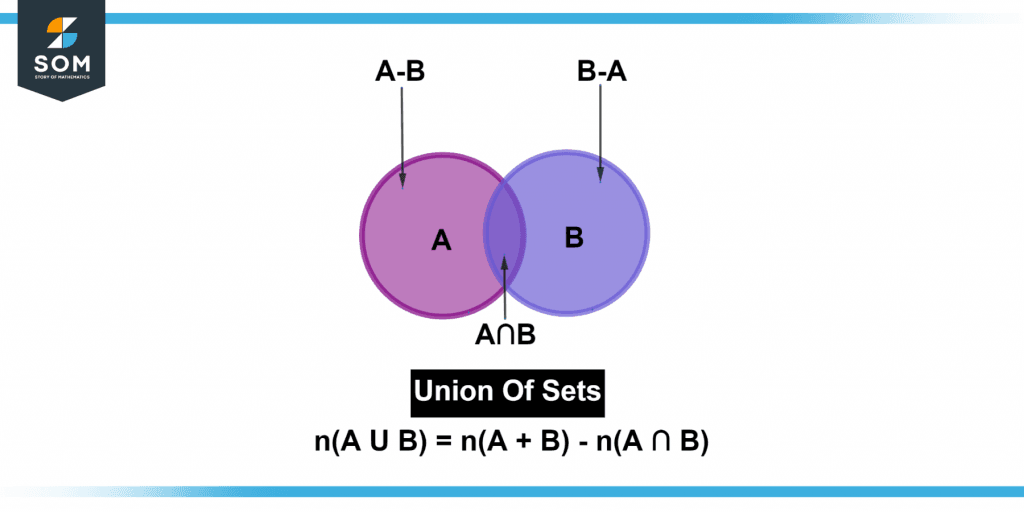
Figure 3 – Representation of a union set.
- A Finite Set’s Power Set
A quantifiable finite set has a countable power set. We can do one-to-one mappings of the resulting set, P(S), with actual figures for a natural set of numbers. When used alongside the union of sets, intersection of sets, and complementary of sets, the function P(S) of set S indicates a Boolean algebra example.
Boolean algebra deals with logical operations on binary variables. The binary integers used to represent the truths of the Random variables are 1 for true and 0 for false. While Boolean algebra focuses on logical operations, introductory algebra works with numeric operations.
Non-empty Finite Set
This set either has many elements or provides the beginning or finish. The number of items we use to represent it is called n(A), so if n(A) is a natural integer, then the set is said to be finite.
A is a collection of a country’s population numbers.
The population of this country is hard to estimate, although it’s somewhere close to a natural amount. Therefore, it qualifies as a non-empty measure used to determine.
Suppose B is a collection of natural numbers below n. Therefore, n is the number of data points of set B.
B = {1, 2, 3, …, n}
Z = z1, z2, …, zn
Where I is an integer between 1 and n, X = {Z: x I $\in$ B, 1 < i < n}.
Is It Possible To Define an Empty Set as a Finite Set?
Let’s first define an empty set.
A set without elements is said to be empty and is denoted by one of the following symbols, which indicates that there are none in the set:
A = {} Or ∅
Since the empty set contains no elements and the finite set contains a calculable number of elements, the number of elements is definite.
Therefore, an unfilled set is finite when its cardinality is 0.
Examples of Finite Sets
Below are some examples of finite number sets.
Example 1
Consider the finite set A = 2, 3, and 4 as an example. Show that subset b = 2, 3 is a finite set.
Solution
There are four elements in Set A = 2, 3, and 4, and they are all natural integers.
Considering this subset b = 2, 3 right now.
This subset s is likewise a finite set since its first and second elements are natural numbers.
Example 2
Think about the finite number sets X = 1, 3, 5, 7 and Y = 2, 4, 6, 8. Show that their union is a finite set as well.
Solution
The limited sets X and Y both contain natural numbers.
This is how their union might be expressed:
X U Y = {1,3,5,7} U {2,4,6,8}
X U Y = A = {1,2,3,4,5,6,7,8}
Set A, which represents the combination of X and Y, has identical items from the finite sets, and they are both natural numbers. As a result, the union of collections A & B is indeed a subset.
All images are made using GeoGebra.
