JUMP TO TOPIC
Frequency|Definition & Meaning
Definition
Frequency is defined as the number of incidents of a recurring event occurring in a specific time interval. In wave propagation, it is defined as the number of wave cycles that pass through a point in one second. It defines the number of oscillations of a periodic signal that occur per unit second. It is denoted by “f.”
Figure 1 shows two waves with different frequencies.
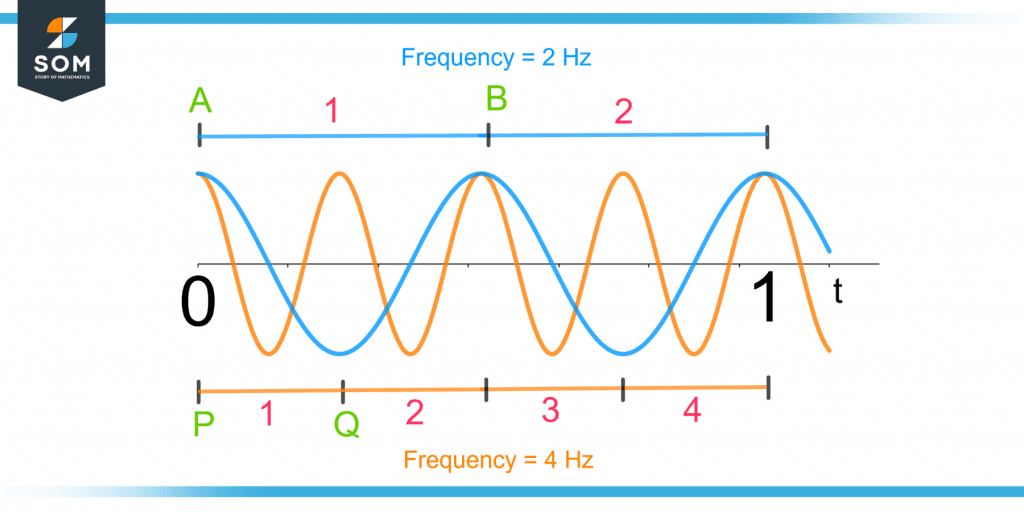
Figure 1 – Demonstration of Frequency of Two Waves
The orange wave has a higher frequency than the blue wave as more repetitions of a wave pattern are observed compared to the blue wave.
The orange wave pattern from point P to Q repeats four times in one second hence its frequency is 4 Hz. Similarly, the wave pattern of the blue wave from point A to B recurs two times per second, therefore having a frequency of 2 Hz.
The wave pattern from A to B and P to Q is known as the wave cycle. The greater the number of wave cycles passing in one second, the higher the frequency. A higher frequency increases the speed of wave propagation.
Unit of Frequency
The frequency unit is named after Heinrich Rudolf Hertz, a German physicist of the nineteenth century. Its unit is “Hertz” abbreviated as “Hz” which is equal to one cycle per second (/s).
Frequency of Periodic and Aperiodic Signals
A periodic signal repeats itself after a specific interval of time and has a definite shape. Whereas, an aperiodic signal does not recur at a regular time interval. It is also known as a non-periodic signal.
The periodic signal has a single frequency whereas an aperiodic signal has multiple frequencies spread over a continuous range.
Frequency in Different Types of Mechanical Waves
A mechanical wave transfers energy through a medium by the oscillation of matter. There are two types of mechanical waves depending upon the motion of wave particles. The frequency of both waves is discussed below.
Transverse Waves
The particles of a transverse wave move perpendicularly to the direction of wave propagation. Examples of transverse waves are light waves, radio waves and water waves formed when a stone is thrown into it.
The particles undergo a to-and-fro motion about their mean position. Figure 2 shows a transverse wave.
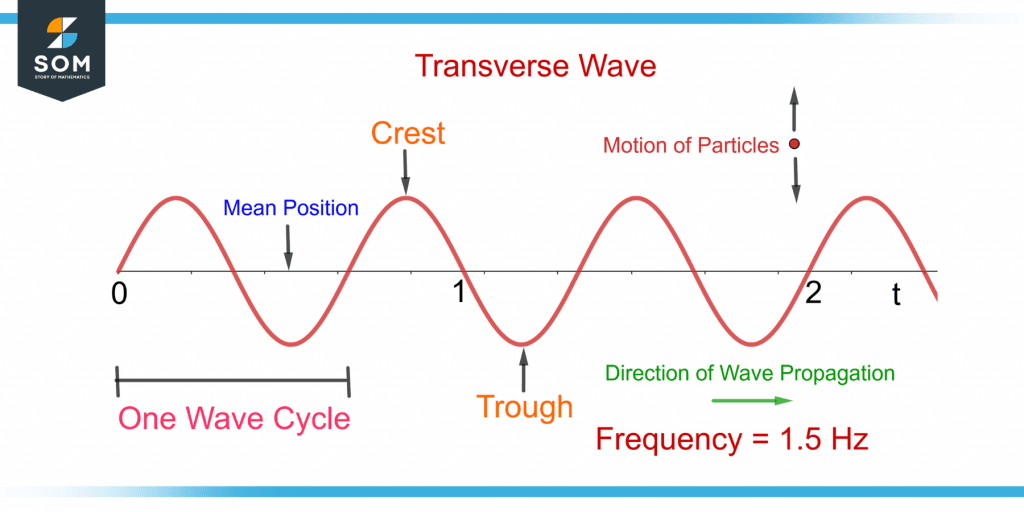
Figure 2 – Demonstration of a Transverse Wave and its Frequency
The maxima and minima of the transverse are known as the crest and trough respectively. The wave from crest to crest or trough to trough makes a complete wave cycle. As a one-and-a-half wave cycle passes per second in the above figure, the frequency of the wave will be 1.5 Hz.
Longitudinal Waves
A longitudinal wave propagates parallel to the motion of the wave particles. An example of longitudinal waves is sound waves. Figure 3 shows a longitudinal wave.
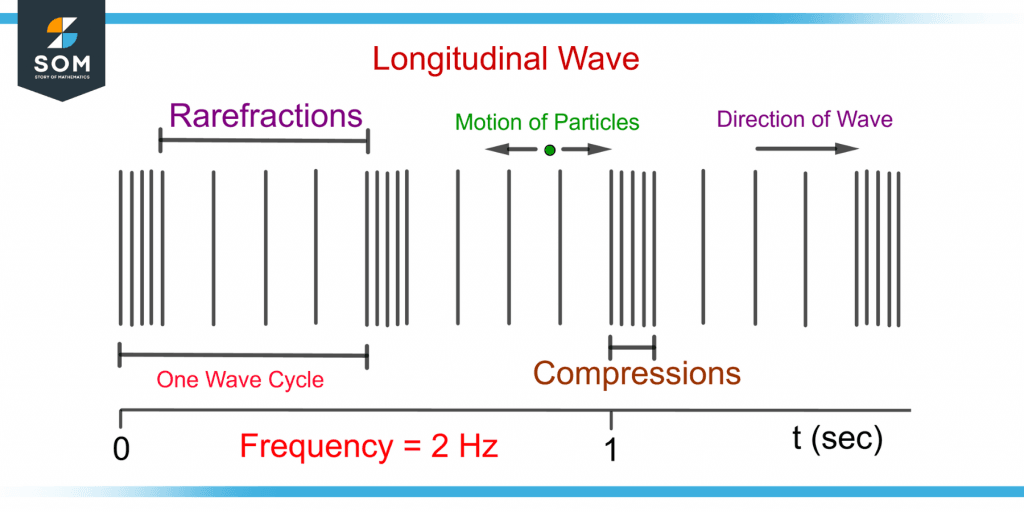
Figure 3 – Demonstration of a Longitudinal Wave and Its Frequency
The wave particles of longitudinal waves have back-and-forth motion. It consists of compressions and rarefactions as shown in the figure. One wave cycle consists of one compression and one rarefaction.
The frequency of the periodic longitudinal wave is 2 Hz as two wave cycles pass through a point in one second.
Human Hearing Range of Frequency
Human beings can hear frequencies ranging from 20 Hz to 20,000 Hz. Infants can hear higher frequency sounds than 20 kHz but lose this sensitivity to high frequency as they grow. Adults can listen to higher frequencies between the range of 15 to 17 kHz.
Frequency in Circular Motion
The angular or circular motion also has a frequency. One complete rotation forming a circle is equal to one wave cycle. So, the frequency in a circular motion can be defined as the number of revolutions per second.
Important Relations of Frequency
The change in factors such as wavelength and time period changes the frequency of the periodic signal. The mathematical relation of the frequency with wavelength and time period is discussed below.
Frequency and Wavelength
The distance between any two adjacent troughs or crests in a wave is called the wavelength. Alternatively, the distance of the wave to complete one wave cycle is also known as the wavelength. It is denoted by lambda(λ) and is measured in meters(m).
The frequency and wavelength are mathematically related as follows:
c = fλ
The product of frequency f and wavelength λ gives the speed of light c. The speed of light is equal to 3 ✖ $10^8$ m/s. We can write the above equation as:
f = c/λ
It shows that increasing the frequency decreases the wavelength and vice versa. Hence, frequency and wavelength are inversely proportional.
Figure 4 shows two waves with their frequency and wavelength.
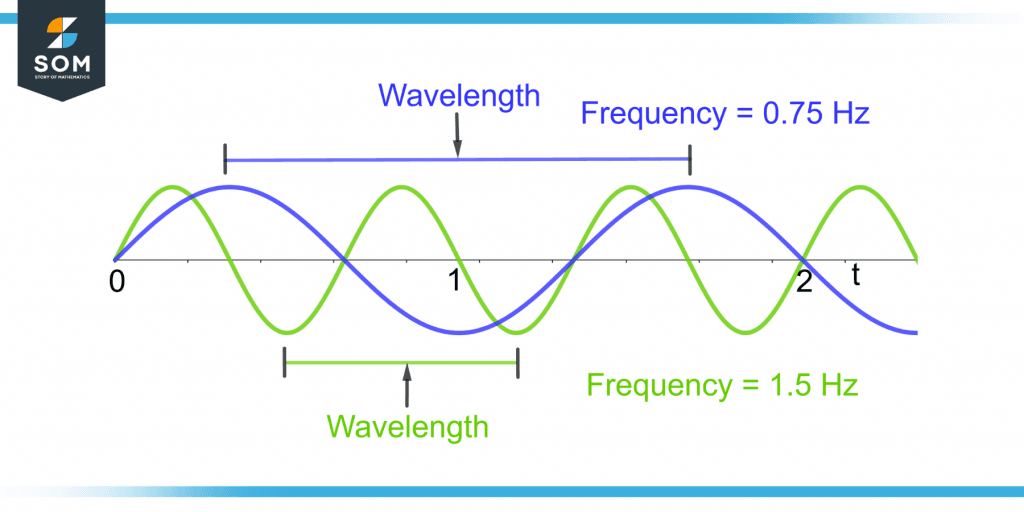
Figure 4 – Comparison of Frequency and Wavelength of Two Waves
The blue wave has a greater wavelength as compared to the green wave. So, the frequency of the blue wave(0.75 Hz) will be less than that of the green wave(1.5 Hz).
Frequency and Time Period
The time taken by a wave cycle to pass from a fixed point is called the time period. The period T and the frequency f are mathematically related as follows:
f = 1/T
Both are reciprocals of each other. It means that period and frequency are inversely related to each other. The unit of T is seconds.
Figure 5 shows the same waves as figure 4 for their time periods and frequencies.
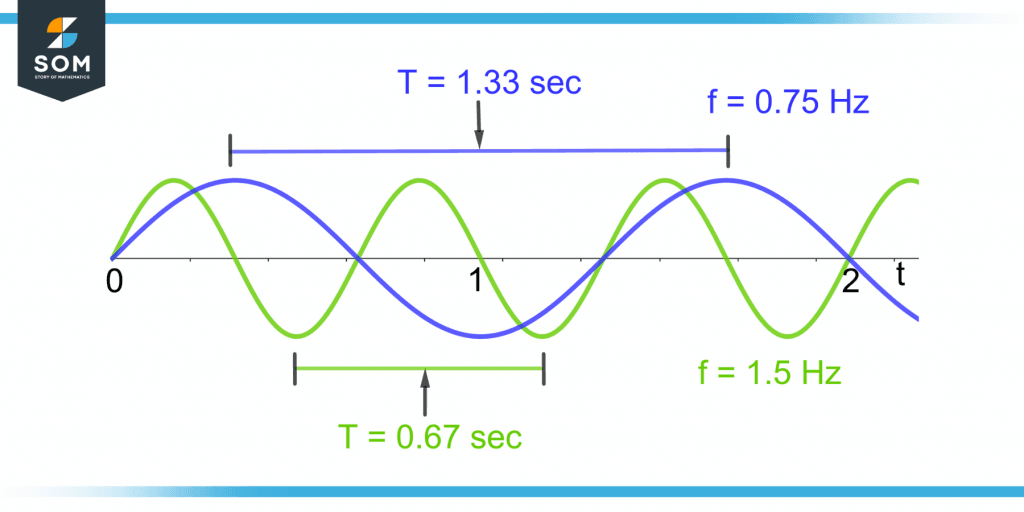
Figure 5 – Comparison of Frequency and Time Period of Two Waves
The green wave with a higher frequency has a less period (0.67 sec) whereas the lower frequency blue wave has a greater period(1.33 sec).
Examples of Frequency Related Problems
Example 1 – Frequency and Wavelength
Calculate the frequency of a wave if its wavelength is 1000 meters.
Solution
From the given data,
λ = 1000 m
The formula for frequency f and wavelength λ is:
λ = c/f
It can also be written as:
f = c/λ
Here,
c = 300,000,000 m/s
Placing the values in the above equation gives:
f = 300,000,000 / 1000
f = 300,000 Hz
f = 300 kHz
So, the frequency of the wave with a wavelength of 1000 m is 300 kHz.
Example 2 – Frequency and Time Period
Calculate the time period of a periodic signal if its frequency is 70 Hz.
Solution
The formula for time period T and frequency f is given as:
T = 1/f
Putting the value of f = 70 Hz, the time period is:
T = 1/70
T = 0.0143 sec
So, the time period of a wave with a frequency of 70 Hz is 0.0143 sec.
All the images are created using Geogebra.
