JUMP TO TOPIC
Interior Angle|Definition & Meaning
Definition
Angles that are inside a shape are referred to as interior angles, and interior angles can also refer to angles that are located in the region enclosed by two parallel lines and a transversal.
From the basic polygon, a triangle, through the polygon with an unlimited number of sides, n, the sides of polygons converge in space. Each intersection of sides produces a vertex with both an interior and an exterior angle. Polygon’s interior angles are contained within the polygon.
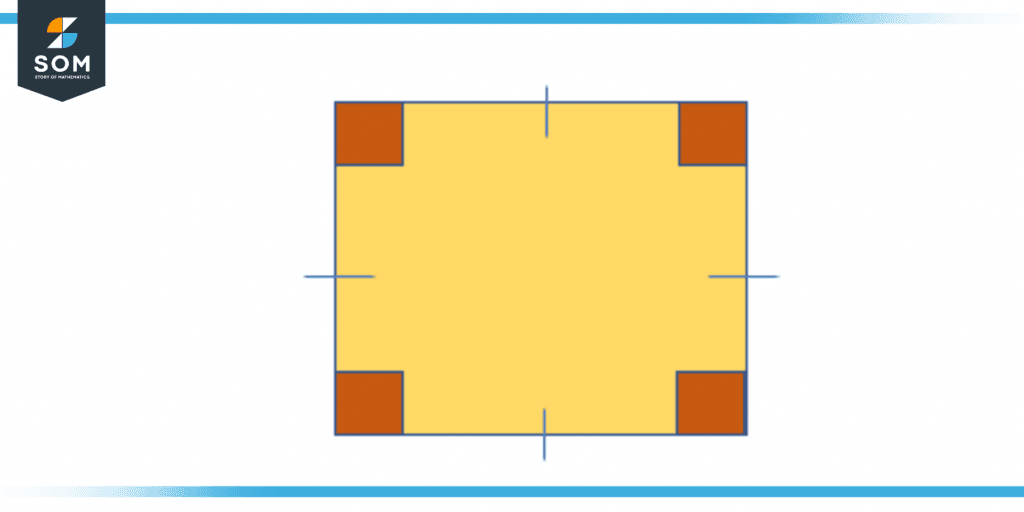
Figure 1 – Interior angle of a square (Regular Quadrilateral)
What Is Interior Angle?
In geometry, there are two ways to create internal angles. One occurs within a polygon, while the other occurs when a transversal cuts parallel lines. On the basis of their dimensions, distinct types of angles are distinguished. Other sorts of angles are characterized as pair angles because they exist in pairs to demonstrate a particular attribute. Interior angles are an example.
Interior angles can be defined in two ways:
- Interior Angles of a Polygon
- Interior Angles of Parallel Lines
Interior Angles of a Polygon
The figure created by combining the two rays at their same terminal is referred to as an angle in mathematics. An interior angle is a shape’s internal angle. The closed shape with sides and vertices is a polygon. All of the inner angles of a regular polygon are equal to one another. For instance, a square has interior angles that are all exactly right angles, or 90 degrees.
A polygon’s internal angles are proportional to the number of sides. Angles are typically expressed in terms of degrees or radians. Therefore, if a polygon has four sides, it also has four angles. Additionally, the total internal angles of various polygons vary.
We refer to the angles contained within a shape, most commonly a polygon, as its inner angles.
The figure above shows the interior angle of a square each interior angle is 90º. The point where the lines join with one another is the vertex. In a square, each vertex has a 90º angle.
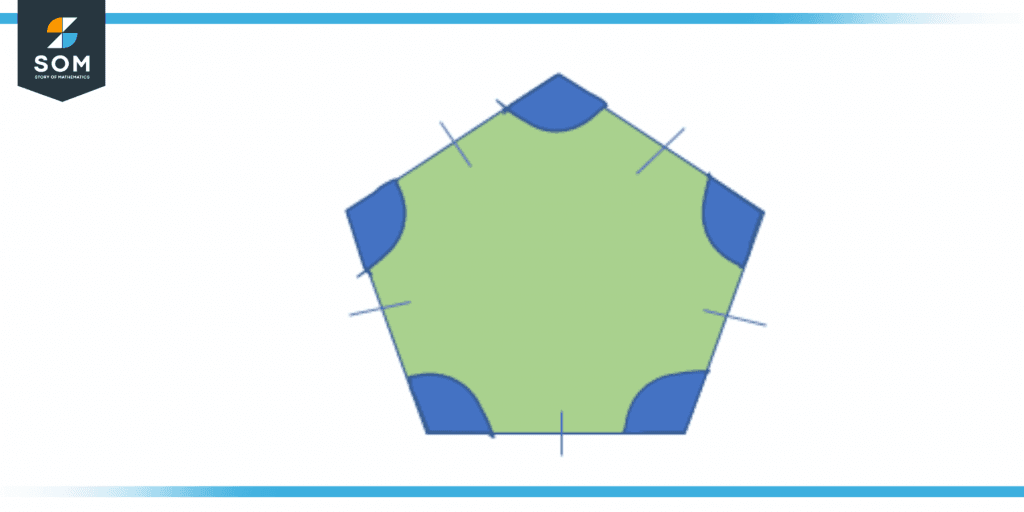
Figure 2 – Interior angles of a regular pentagon
Interior Angles of Parallel Lines
Interior angles are another name for angles that are in the space bounded by parallel lines which are crossed by a line that is called a transversal line. All the angles within these parallel lines along the transversal line are interior angles whereas angles out sIde the parallel line are exterior angles.
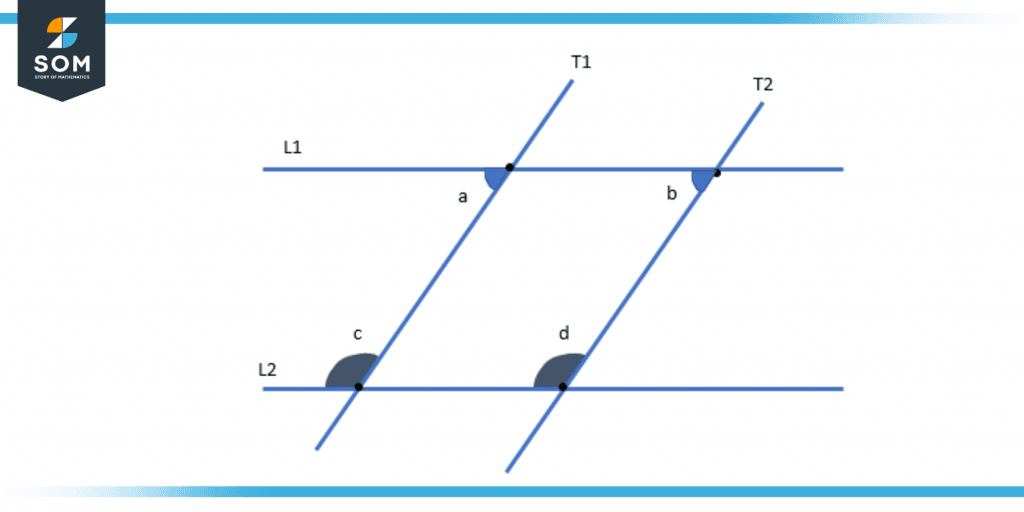
Figure 3 – Interior angles of Parallel Lines
The lines L1 and L2 are parallel to one another in the below diagram, and the lines T1 and T2 are the transversal lines that are cutting both parallel lines. The angles ∠a, ∠b, ∠c, and ∠d all fall into the category of internal angles.
Interior Angle’s Types
When two parallel lines are intersected by a transversal, two different kinds of interior angles are created. These two kinds of interior angles are known as co-interior angles and alternate interior angles.
Alternate Interior Angles
These angles are created when a transversal intersects two parallel lines. The opposing sides of a transversal produce these non-adjacent angles pair. The alternate interior angles paired in the initial image are 1 and 3, and 2 and 4. If a transversal cuts two parallel lines, their lengths are equal.
Co-Interior Angles
On the identical side of the transversal, such angles seem to be the pair of interior non-adjacent angles. Co-interior angle pairs are (1 and 4), and (2 and 3). Additionally known as consecutive interior angles or same-side interior angles, these angles are interior. Co-interior angles also make up a pair of supplementary angles because the sum of two of them is 180 degrees.
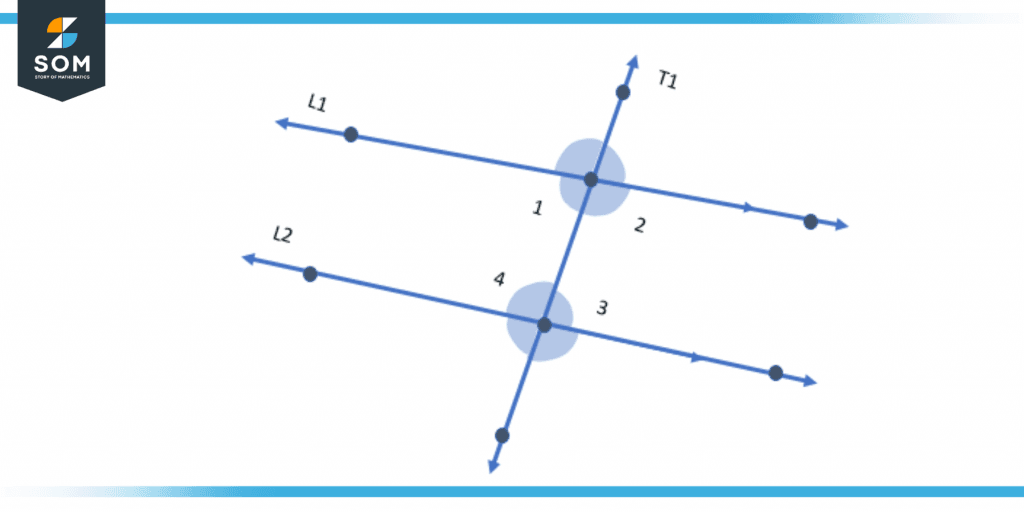
Figure 4 – Alternate and Co-Interior angles
Here ∠1, ∠2, ∠3, and ∠4 are interior angles between two parallel lines L1 and L2, and one transversal line T1.
Interior Angles of a Triangle
Every vertex of a triangle contains three inner angles. These inner angles always add up to 180 degrees. The incenter is the place where the bisectors of all these angles intersect. Due to the fact that the total of the internal angles in a triangle equals 180°, there is simply one right angle and obtuse angle available in any triangle.
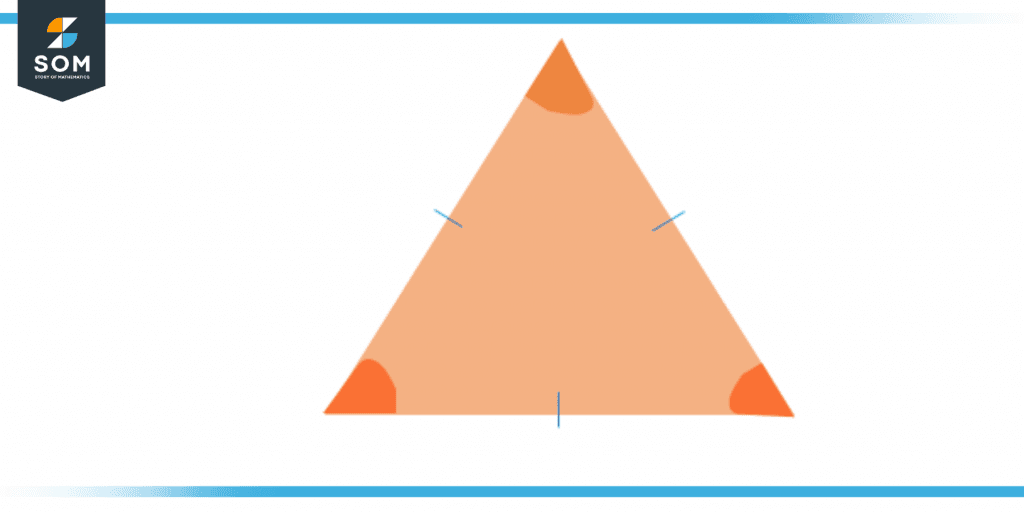
Figure 5 – Interior angle of a triangle
A triangle with three acute interior angles is known as an acute triangle, a triangle that has one interior angle that is obtuse is called an obtuse triangle, and a triangle including one interior angle that is right-angled is known as a right-angled triangle.
Interior Angle Formula
All the sides of a polygon generate a vertex, and this vertex has an exterior and interior angle, from the basic polygon, let’s assume a triangle, to the indefinitely complicated polygon with n sides, such as an octagon. The total of a triangle’s three internal angles is 180 degrees, according to the angle sum theorem. The summation of the interior angles of any polygon is obtained by multiplying two fewer than the number of sides by 180 degrees.
Sum of interior angle = (n-2)x 180º
Here, n is the sides of any shape. Applying this formula to the regular pentagon, the pentagon has 5 sides so putting values in the formula, we get:
Sum of interior angles of a pentagon = (5-2) x180º
Sum of interior angle = 3×180º
Sum of interior angle= 540º
Example 1
Solution
Sum of interior angles = (n-2)x 180º
Sum of interior angle= (8-2) x 180º
=1080º
Example 2
Find the unknown interior angle xº of two parallel lines.
Solution
The unknown angle xº is with a transversal line.
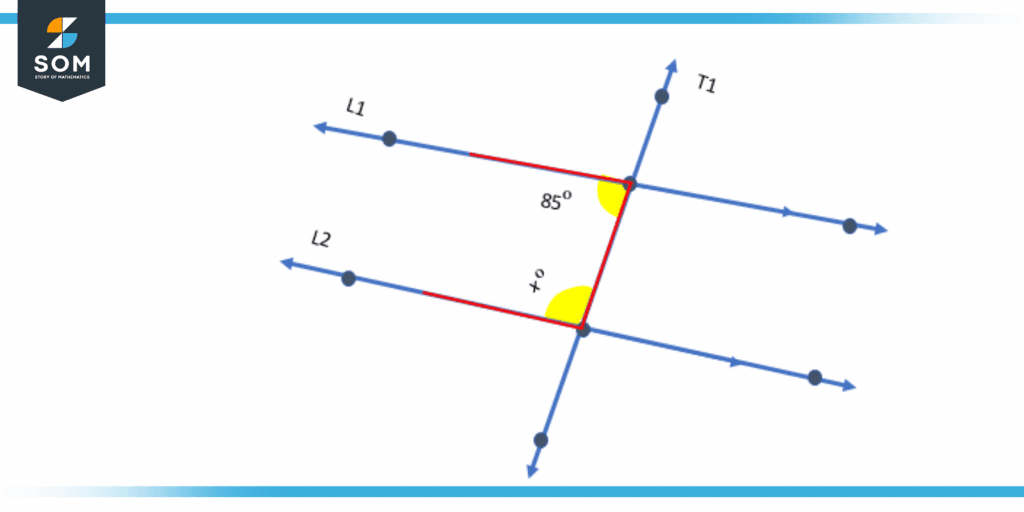
Figure 6 – Unknown interior angle xº between two parallel lines
85º + xº = 180º
xº = 180º – 85º
xº = 95º
All the figures above are created on Geogebra.
