Least Common Denominator|Definition & Meaning

Figure 1: Two fractions having common denominators.

A value used to determine the smallest number that two or more denominators—the bottom value in a fraction—have in common is the least common denominator, often referred to as the least common multiple. In mathematics, especially when dealing with fractions, this concept is fundamental.

Use of LCD

Various fractions with different denominators are summed or subtracted using the least common denominator (LCD). To subtract or add two or more fractions, a common denominator is required. This is so that the fractions can never be added together since the denominators represent the units in which the fraction is measured. 

To make all the denominators equal and enable the addition or subtraction of the fractions, there must be a common denominator for two or more fractions.

For instance, we must first find out the least common denominator before adding the fractions 1/2 and 1/3. The LCD is 6 because it is the least common multiple of 2 and 3. 

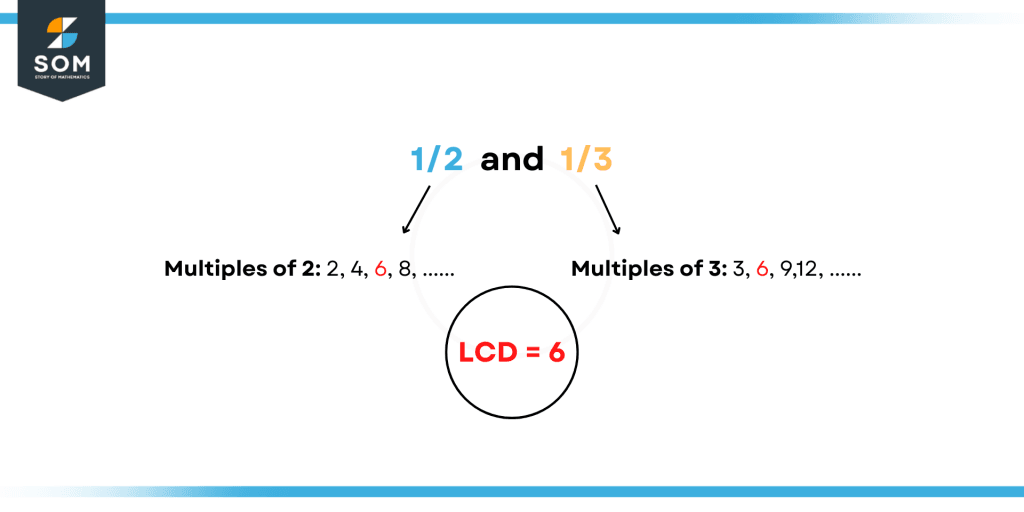
Figure 2: Least common denominator of 1/2 and 1/3.

Then, we can rewrite both fractions using a 6 as the denominator: 1/3 turns into 2/6 and 1/2 into 3/6. Now that the denominators of the two fractions are the same, we can combine them:

3/6 + 2/6 = 5/6

Methods of Finding the Least Common Denominator

There are commonly two methods to find the least common denominator. They are discussed as follows.

Figure 3: Methods to find the least common denominator.

The Common Method

Usually, to determine the least common denominator, one must find the least common multiple of the denominators. We can list the multiples of each number and identify the one that the two numbers have in common the least. 

If there are more than two numbers, we can calculate the LCM of the first two before calculating the LCM of the outcome and the following number, and so on, until we have calculated the LCM of every number.

For example, to find the LCM of 4 and 6, we list out the multiples of each:

4, 8, 12, 16, 20, 24, 28, 32, 36, and so on are multiples of four.

6, 12, 18, 24, 30, 36, 42, 48, 54, and so on are multiples of six.

The smallest multiple that both 4 and 6 have in common is 12, so the LCM of 4 and 6 is 12.

Using the same procedure, we can determine the LCM of three or more numbers by finding the LCM of the result and the subsequent number until we have determined the LCM of all the numbers. 

For instance, we can first determine the LCM of 4 and 6, which is 12, before determining the LCM of 4, 6, and 8. The LCM of 12 and 8 is then discovered to be 24. Thus, 24 is the LCM of 4, 6, and 8.

Prime Factorization Method

Prime factorization can also be used to get the LCM. Finding the prime factorization of each integer allows us to determine the LCM of two numbers by multiplying the greatest power of each prime factor. For instance, we can first determine the prime factorization of each to determine the LCM of 15 and 20:

15 = 3 * 5

20 = 2 * 2 * 5

The LCM is produced by multiplying each prime factor by its maximum power:

LCM of 15 and 20 is equal to 2 * 2 * 3 * 5 = 60.

By following the same procedure, finding the LCM of the outcome and the subsequent number until we have discovered the LCM of all the numbers, we can determine the LCM of more than two numbers.

Properties of Least Common Denominator

In the field of mathematics, apply the idea of the least common denominator (LCD) to add or subtract fractions with various denominators. It is the denominator of two or more fractions with the smallest common multiple. The least common denominator has the following characteristics:

• Uniqueness: The LCD of a collection of fractions is unique, which means that for a given set of denominators, there is only one smallest common multiple.
• Multiplication: By multiplying the fractional denominators, the LCD can be calculated.
• Divisibility: Each of the fractions’ denominators must be able to divide the LCD.
• Positive Value: The LCD must always have a positive number.
• Monotonicity: As the number of fractions in a set of fractions increases, so does the LCD.
• Commutativity: It makes no difference what order the denominators are multiplied to produce the LCD.
• Associativity: The LCD of a set of fractions is associative, which means that the result is unaffected by the arrangement of the denominators.
• Transitivity: The LCD of all three denominators is the case where a common multiple of two denominators is also a multiple of a third denominator.

The LCD is not necessarily the result of the denominators; it is vital to remember this. Given the requirement that the LCD be the smallest common multiple, it can be a multiple of numbers apart from the denominators along with the LCD.

It is necessary to convert each fraction to an equal fraction with the same denominator, which is the LCD, in order to add or subtract fractions. As a result, we can add and subtract the fractions as if they had the same denominator. When it comes to adding or subtracting fractions with various denominators, the LCD is a useful technique.

The least common denominator is a useful mathematical concept that enables us to add and subtract fractions with various denominators. Its properties, such as uniqueness, divisibility, and positivity, make it a valuable resource for tackling fraction-related mathematical problems.

Solved Examples Involving the Least Common Denominator

Example 1

Calculate the least common denominator of 1/4 and 1/6.

Solution

These two fractions have the denominators 4 and 6, respectively. 4 and 6 have the following multiples:

Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, and so on.

Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, and so on.

We can observe from this list of multiples that 12 is the least common multiple. Therefore, these two fractions’ least common denominator is twelve.

Example 2

Find the least common denominator of 1/8 and 1/12 by using the method of prime factorization.

Solution

These fractions have denominators of 8 and 12.

The prime factorizations of these two denominators must now be determined:

8 has the following prime factors: 2 x 2 x 2

12 has the following prime factors: 2 x 2 x 3

The prime numbers 2 and 3 appear the most frequently: 2 x 2 x 2 in 8 and 3 in 12.

We now need to multiply each factor separately:

2 × 2 × 2 × 3 = 24

Thus, 24 is the least common denominator of the fractions 1/8 and 1/12.

All images/mathematical drawings were created using GeoGebra.