JUMP TO TOPIC
Median of Triangle|Definition & Meaning
Definition
A triangle median is a line segment that connects one vertex of the triangle to the midway of the opposing side, thereby bisecting that side. Each triangle has three medians, one for each vertex. These medians cross just at the triangle’s centroid.
A line segment runs from a vertex (edge point) to an opposing side’s midway. A triangle contains three medians, each of which intersects at a particular location known as the “centroid.”
Figure 1 below shows the median of a triangle.
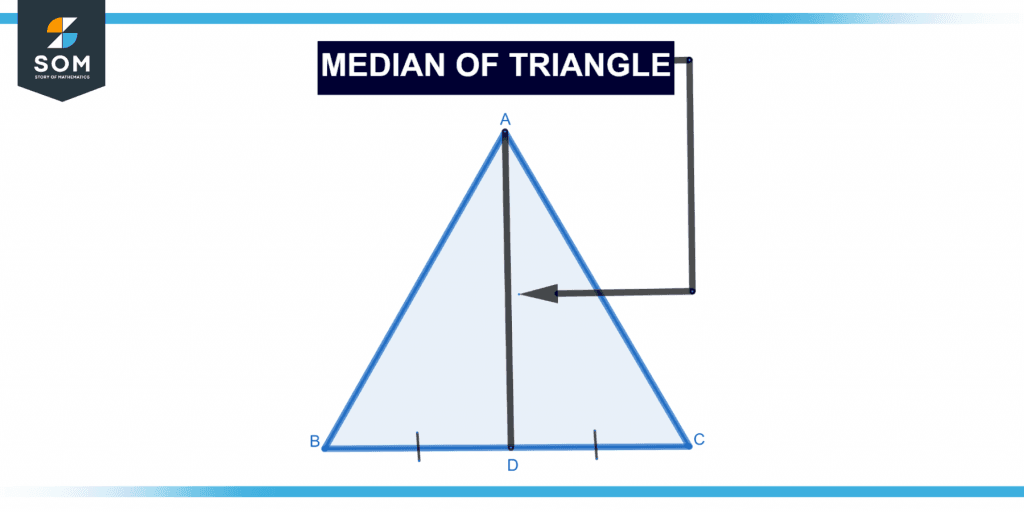
Figure 1 – Representation of the median of a triangle.
Median of Triangle
A triangle median is a line segment that connects a vertex to the midpoint of the wall opposite that vertex. XY is the median in the image below, splitting YZ into two equal pieces such that XY = YZ.
Properties of Median of Triangle
The following qualities may be used to identify a triangle’s median readily:
- The triangle’s median is a line segment from the vertex of a triangle towards the half of its opposing side.
- It cuts the opposing side in half, separating it into two equal halves.
- The middle of a triangle splits it further into two triangles of equal area.
- A triangle’s three median values meet at a single point regardless of its form or size.
- Each triangle has three medians, one at each vertex. The convergence of three medians forms the triangle’s centroid.
- Every triangle’s median splits into two small triangles with equal areas. In reality, the three medians split the triangle into six equal-area triangles.
Altitude and Median of Triangle
Altitude and median are not the same things. The line segment connecting the vertex and thus the half of the opposite side of the triangle is denoted as the median. Regardless of triangle form, all triangles contain three medians (one for each vertex) that meet at a single point.
The three medians are positioned within the triangle and intersect at a point known as the triangle’s centroid. A median always cuts the opposite side it is established on.
Altitude
A triangle’s altitude is defined as a centerline at a right angle (90°) connecting a vertex to an opposite aspect of a triangle. An altitude is within or even outside a triangle, depending on its kind. Every triangle has three heights (one for each vertex), which converge at the single point known as the orthocenter.
Orthocenter
The orthocenter could be positioned either inside or outside the triangle. An altitude doesn’t need to cut it through the opposite side from whence it is formed.
How To Find Triangle’s Median?
The median of a triangle may be calculated using a simple procedure that applies to all three medians. Let’s peek at the equation for measuring the distance of each midpoint.
Formula
The formula of the first median of the triangle is as follows: where ma is the median of a triangle, the triangle’s sides are x, y, and z, and the median is created on the side ‘x’:
\[m_{x}=\sqrt{\frac{2y^{2}+2z^{2}-x^{2}}{4}}\]
The formula for 2nd median of the triangle is as follows: the median of such a triangle is my, the triangle’s sides are a, b, and c, and the median is created on side ‘y’:
\[m_{y}=\sqrt{\frac{2x^{2}+2z^{2}-y^{2}}{4}}\]
The equation for the 3rd median of the triangle is just as follows: where the triangle’s median is mz, the triangle’s sides are x, y, and z, and the median is generated on side ‘z’:
\[m_{z}=\sqrt{\frac{2x^{2}+2y^{2}-z^{2}}{4}}\]
Figure 2 below shows the formula for the median.
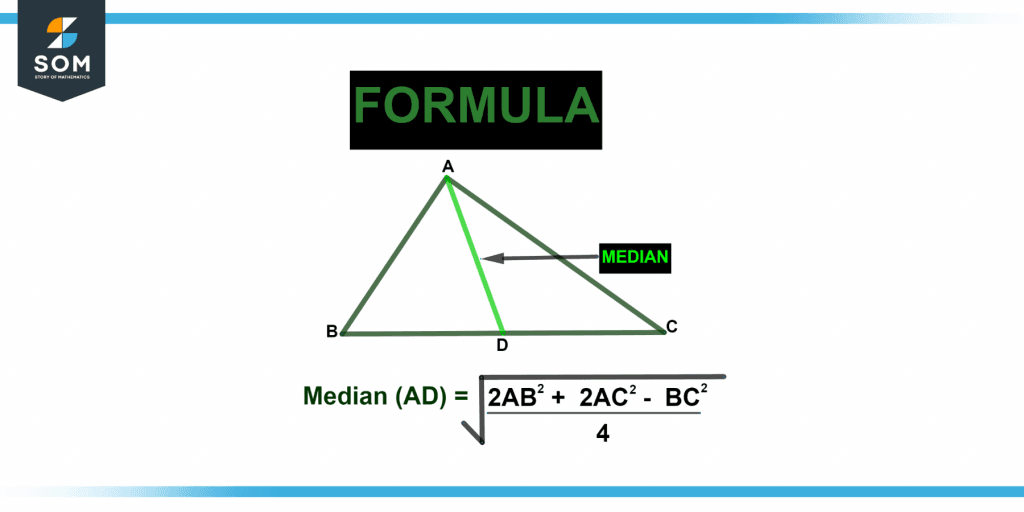
Figure 2 – Formula for a median of a triangle.
Finding the Median of the Triangle With Coordinates
When we have the coordinates of a triangle’s three vertices, we can use the procedures below to calculate the length of the triangle’s median.
Step 1: To use the coordinates of vertices of a triangle, locate the coordinates of a middle of a line segment that forms the median created. The midpoint formula can be used to do this.
Step 2: Once the midpoint coordinates are determined, use the distance formula to calculate the extent of the median, where one end is the vertex where the median begins, and the other is the midway of the reference line upon which the median is constructed.
Step 3: The median length may be estimated using the distance formula.
Figure 3 below shows the Median of the Triangle with the coordinates.
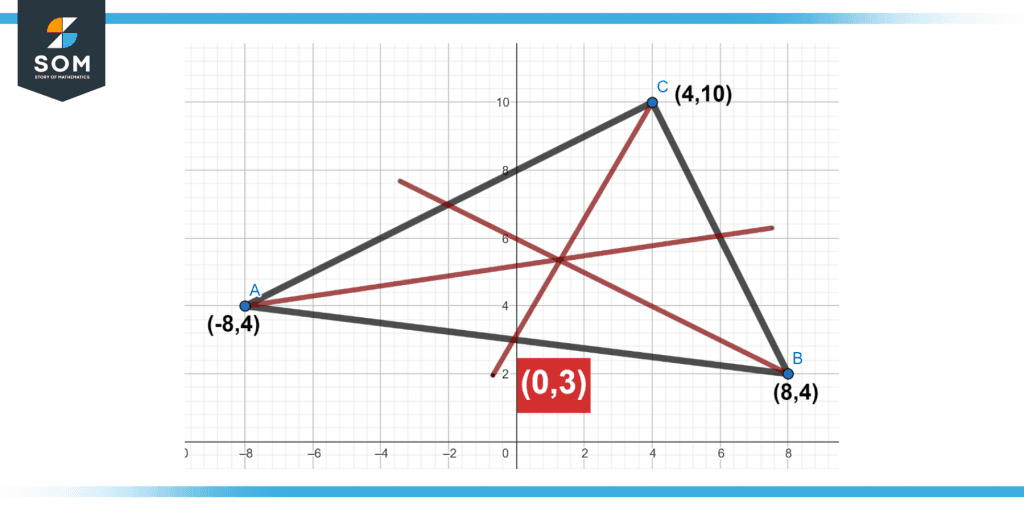
Figure 3 – Representation of the median of a triangle using coordinates.
Characteristics of the Median of a Triangle
Some of the characteristics of the median of the triangle are listed below
- Each median splits the triangle into two smaller triangles of equal size.
- The triangle’s center of gravity is the centroid (where they meet).
- A triangle’s perimeter is bigger than the sum of its three medians.
- Because the corresponding sections of congruent triangles were congruent, the medians for congruent triangles are identical if the two triangles are congruent.
Examples of Median of Triangle
The following solved examples of a median of a triangle will further help you understand the concept.
Example 1
Determine if the following assertions are true or untrue using the characteristics of a triangle’s median.
a.) If the three sides of the triangle are a, b, and c, and the median is present on side a, the median for the triangle formula that’s also employed is:
\[m_{a}=\sqrt{\frac{2b^{2}+2c^{2}-a^{2}}{4}}\]
b.) The convergence of three medians forms the orthocenter of a triangle.
c.) The middle of such a line segment is where the median crosses the opposing side.
Solution
a.) This is right; the formula is valid.
b.) False; the point of convergence of three medians forms the triangle’s centroid. The orthocenter is the place at which a triangle’s elevations connect.
c.) True, where the median crosses the opposing side is the line segment’s midway.
Example 2
G is the centroid of the provided triangle ABC, where BC = 10 units. Estimate the length for BD.
(Give an indication: AD is the triangle’s median.)
Solution
Triangle ABC’s medians are AD, CE, and BF, and D is the midpoint for BC since AD is indeed the median. BC Equals 10 units. Hence BD Equals DC Equals 5 units. As a result, BD Equals 5 units.
All Images are made using GeoGebra.
