Pascal’s Triangle | Definition & Meaning

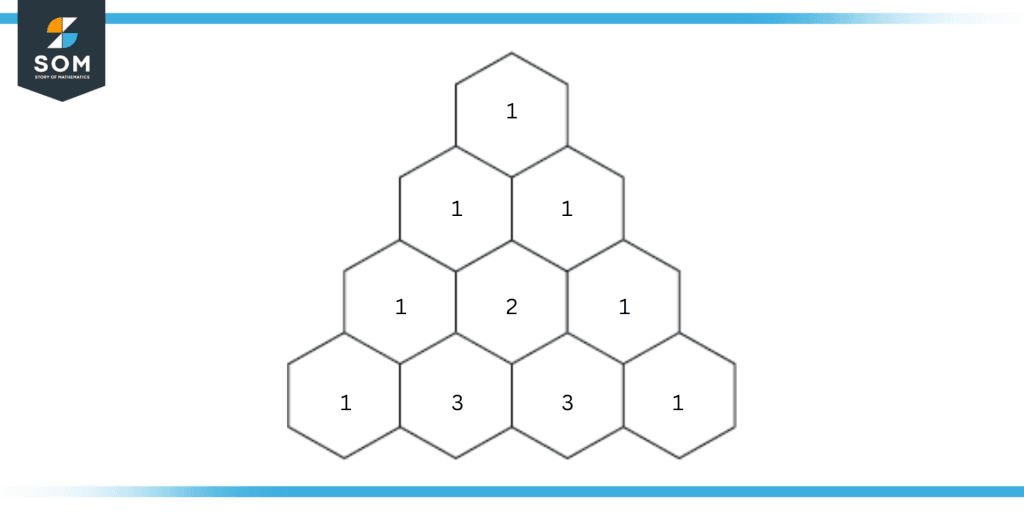
Figure 1: A four-row Pascal’s triangle. 

The following expression gives the formula for Pascal’s triangle:

\[ \mathsf{C (n, k) = \frac{n!}{k! (n – k)!}} \]

History of Pascal’s Triangle

Blaise Pascal published the Treatise on the Arithmetical Triangle, also known as Pascal’s Triangle, in 1653. Although the triangle was separately discovered in the eleventh century by mathematicians in Persia and China, Pascal is primarily credited with discovering its features and uses.

Yang Hui’s triangle is the name given to Pascal’s triangle in China. The Chinese mathematician Jia Xian first made the triangle known in the early 11th century.

The Persian poet, astronomer, and mathematician Omar Khayyam also mentioned it. The triangle is also known as the Khayyam triangle or the Khayyam-Pascal triangle in Iran.

The binomial theorem for non-negative integer exponents was one of many theorems concerning the triangle that was understood. This is the first printed instance of the triangle in Europe, where it initially appeared as the epigraph of a book written by Petrus Apianus.

Pascal made numerous contributions to mathematics, including this triangle. Additionally, he developed important geometric theorems, uncovered the roots of probability and calculus, and created the Pascaline calculator. However, his work on the Pascal triangle is what made him most famous.

Construction of Pascal’s Triangle

Starting at row 0 and writing only the number 1 will result in the triangle being built the simplest. Add the number immediately above and to the left of the number with the number above and to the right of it to get the numbers in the subsequent rows.

Replace the missing number here on the left or right with a zero and continue adding if neither side has any numbers. 

Properties of Pascal’s Triangle

A Pascal’s triangle has the following properties:

• The Pascal triangle is a symmetrical shape.
• Triangle’s bottom and the number 1 are the only elements on either side.
• Outside of the triangle, all numbers are assumed to be 0.
• Along diagonals, the Fibonacci numbers can be observed.

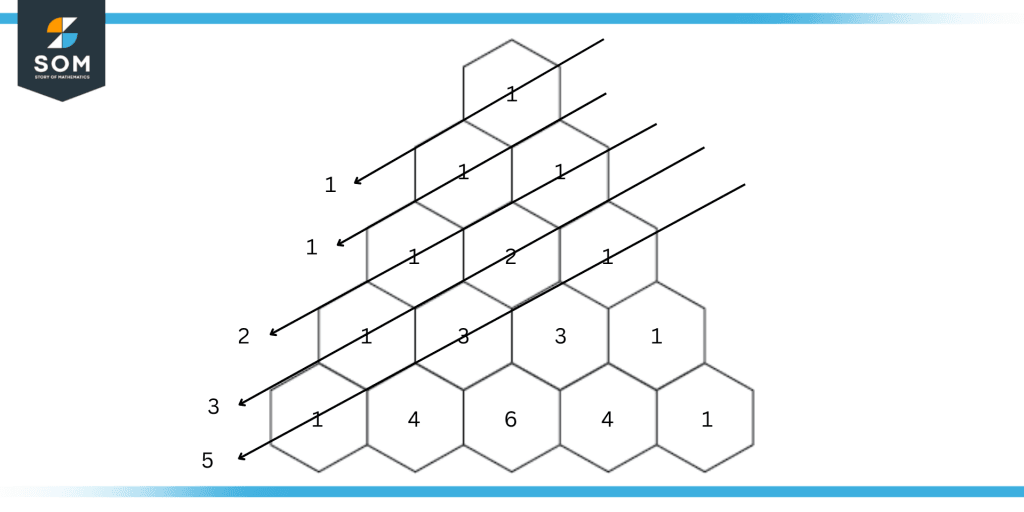
Figure 2: Fibonacci sequence in Pascal’s triangle.

• The sum of the numbers right above it yields all the entries in Pascal’s triangle.
• The same row of numbers adds up to powers of 2. This is the result of the binomial theorem.
• Every row’s summation is equal to two raised to the power of n.
• Each row displays the digits that are powers of 11.
• Up until the center of the row, the numbers increase before decreasing to 1.
• The fact that Pascal’s triangle’s nth row and rth number are actually C(n, r) may be the most crucial finding.

Applications of Pascal’s Triangle

Mathematicians use Pascal’s triangle in many different areas, including algebra, probability, combinatorial optimization, statistics, and more. The combinations can be computed using Pascal’s triangle.

Pascal’s triangle can demonstrate how many different ways we can mix heads and tails in a coin flip. This can then demonstrate the likelihood of any combination.

We can utilize n+1 to decide which row to employ, where n is the power of the binomial to decide which row to employ. As an alternative, we may treat the first row as 0, and then we could choose the row in Pascal’s triangle that is denoted by the power. Take the following binomial expansion as an illustration.

(x + y)² = 1x²y⁰ + 2x¹y¹ + 1x⁰y² = 1x² + 2xy + 1y²

We get the coefficients 1, 2, and 1 through this expansion. This is equivalent to Pascal’s triangle’s third row. Since the power of the binomial, as we can see, is 2, using n + 1 gives us the number 3, which does equate to the third row used.

Pascal’s triangle is also utilized in probabilistic techniques and combination calculation.

Using Pascal’s Triangle on a Real-Life Scenario

Pascal’s triangle consists of all the binomial coefficients. Using the triangle, you may determine how many different methods there are to choose two out of five unique objects. Beginning at the top left corner of the triangle, proceed 5 spaces along the 1s before moving across 2 spaces. You ought to receive a value of 10.

The counting process is an additional application of Pascal’s triangle. Let’s imagine you want to choose two items from a list of five. How many options are there for choosing these items?

This value can be observed directly thanks to Pascal’s triangle.

We are given six values by moving to the triangle’s 5th row (1 5 10 10 5 1). Each of these numbers corresponds to selecting a specific number of objects, starting at zero, from a group of five.

In order to identify two units from a batch of five, we can return to our initial problem by using Pascal’s triangle. By counting three spots to the left (since 0 is included), we arrive at 10, equal to C(5, 2) or the number of possibilities for arranging two items in a collection of five items.

Examples Solved Using Pascal’s Triangle

Example 1

Find out the coefficient of the third term of (x – 3)⁴ using Pascal’s triangle.

Solution

Instead of using the tedious approach, we can use Pascal’s triangle pattern to find out the coefficients of the expanded expression.

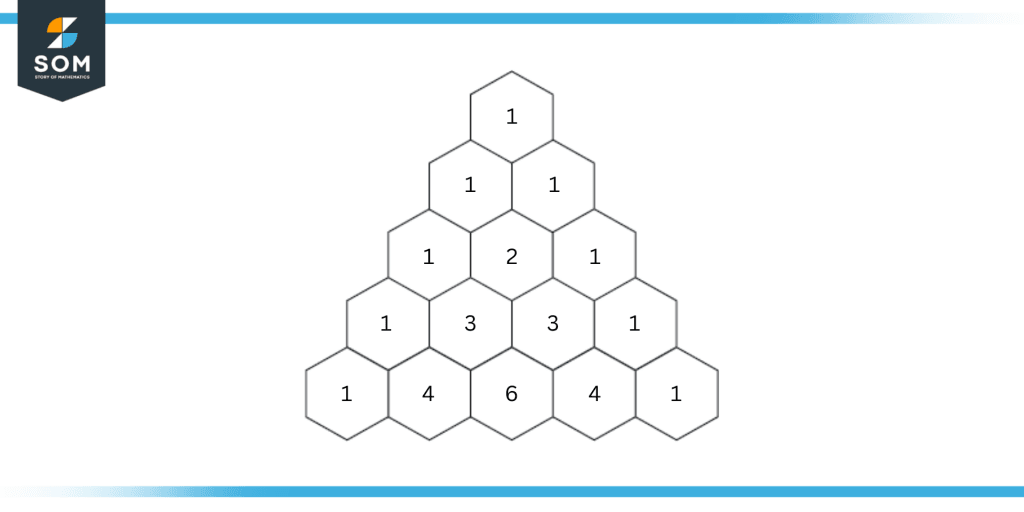
Figure 3: A five-row Pascal’s triangle used for finding out the third term of the above expression.

Hence, the terms are 1x⁴, 4x³, 6x², 4x¹, and 1.

The coefficient of the third term is 6. 

Example 2

Expand (x + 2y)³ using Pascal’s triangle.

Solution

Let us again use the same pattern and find out the result.

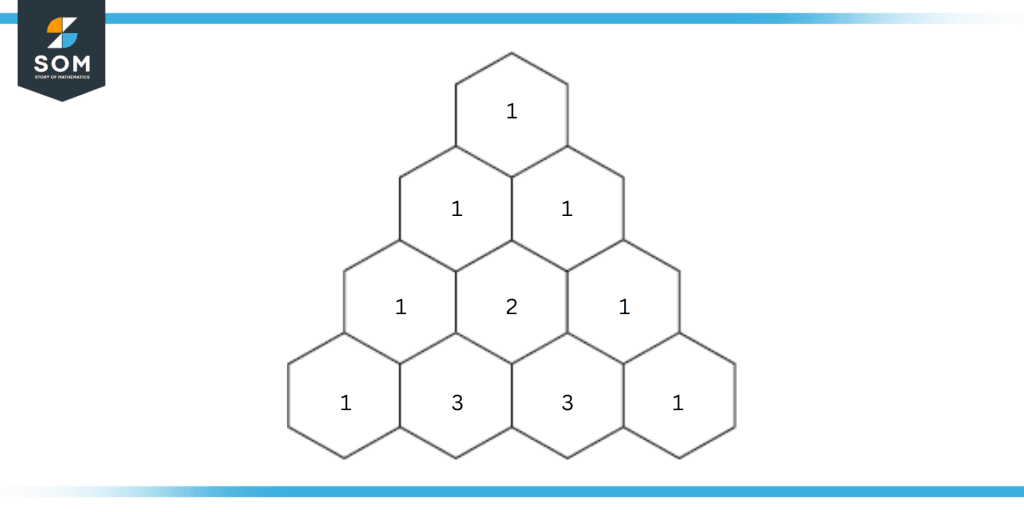
Figure 4: A four-row Pascal’s triangle used for the expansion of the above example.

Therefore, our terms are 1x³, 3x², 3x¹, and 1.

Now, the next step is to multiply each term by 2y and add them:

1x³(2y)⁰ + 3x²(2y)¹ + 3x¹(2y)² + 1(2y)³

Hence, the following is our result:

x³ + 6x²y + 12xy² + 8y³

Example 3

Expand (2x – 4)⁴ using Pascal’s triangle.

Solution

This example is similar to the previous one. So let us write the pattern again.

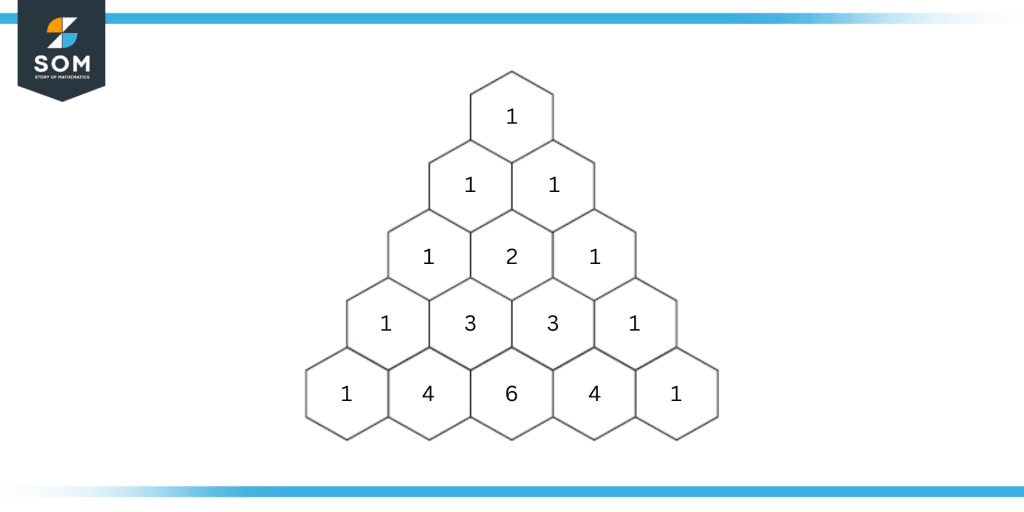
Figure 5: A five-row Pascal’s triangle used for the expansion of the above example.

Hence, the terms are 1x⁴, 4x³, 6x², 4x¹, and 1.

Ultimately, the above expression becomes:

1(2x)⁴(-4)⁰ + 4(2x)³(-4)¹ + 6 (2x)²(-4)² + 4 (2x)¹(-4)³ + 1(2x)⁰(-4)⁴

16x⁴ – 96x³ + 216x² – 216x + 81

All images/graphs were created with GeoGebra.

Parity Definition < Glossary Index > Pentagonal Number Definition