Pentomino|Definition & Meaning

Pentominoes are figures that operate with five square blocks joined edge to edge to form different mixtures. There are twelve achievable shapes in a set of distinctive pentominoes that are characterized by T, U, V, W, X, Y, Z, F, I, L, P, and N. The word FILiPiNo and the end of the alphabet, TUVWXYZ is a technique that is being used by people easily remember the pentominoes letters set. 

To see what counts as a pentominoThere are some rules. If you rotate a shape and then both shapes look the same, that does not count as pentomino also if you flip a shape and then both shapes look the same then it will also not count as pentomino.

About Pentominoes

Take five identical squares. Arrange the squares so that at least one edge of each square is connected to at least one of the other four squares. Find all such positions, then remove any arrangement that when turned or flipped becomes the same as any other arrangement. There are only 12 separate arrangements or pieces that can be made.

Each pentomino has a single-letter name to it that, on one point, produces the shape of that piece, as shown below.

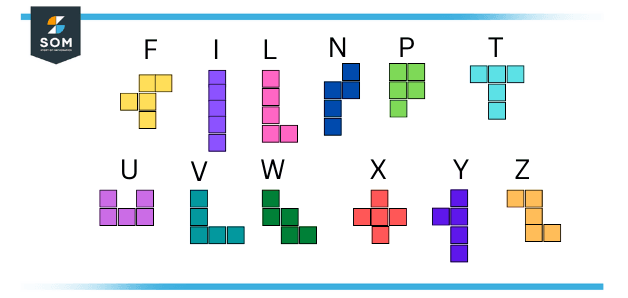
Figure 1 – Twelve Pentominoes Pieces

Constructing Rectangular Dimensions

A typical pentomino puzzle is to build a rectangle with the pentominoes, i.e. making it without gaps or without overlapping. A pentomino has an area of 5 unit squares, and there are 12 pentominoes, so the box must be 60 units. 3×20, 4×15, 5×12 and 6×10 are the only possible sizes.

In 1960, Colin Brian Haselgrove and Jenifer Haselgrove solved the first case which was the 6×10. The exact number of solutions is 2339, excluding trivial variations that are brought by rotating or reflecting of the rectangle, but if we include rotation and reflection of a subset of the pentominoes (which occasionally delivers an extra solution in an easy way). There are 1010 solutions to the 5×12 box, 368 solutions to the 4×15 box, and just 2 solutions to the 3×20 box (one of the two is displayed in the diagram, and the other one can be obtained from rotating the whole block consisting of the alphabets: L, N, F, T, W, Y, and Z pentominoes).

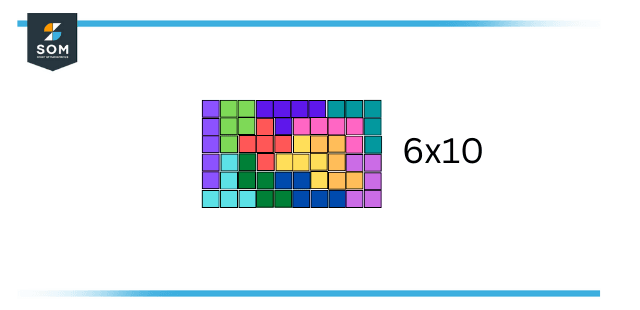
Figure 2 – 6×10 Rectangular Formation

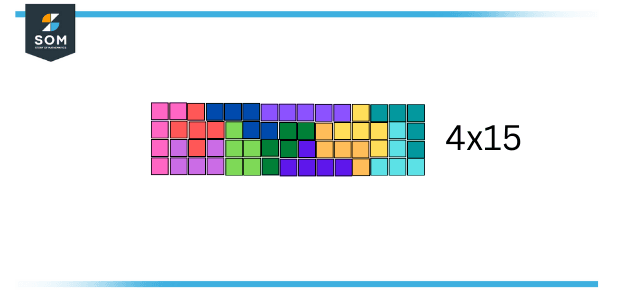
Figure 3 – 4×15 Rectangular Formation

A relatively easy (more symmetrical) to solve the puzzle, the 2×2 hole in the center of the 8×8 rectangle, was solved by Dana Scott in 1958. There are a total of 65 solutions. Scott’s algorithm was one of the foremost applications of a backtracking computer program. The four holes can be placed in any position thanks to the variations of this puzzle. This rule is used by one of the external links.

More than half of such patterns are resolvable, but arranging all pairs of holes separately near the two corners of the board must be one of the exceptions, in such a way that a P-pentomino could only fit both corners, or on the other hand, driving a T-pentomino or U-pentomino in a corner with the end goal that another hole is made.

Symmetry

Pentominoes symmetry is as follows:

• The English alphabet, F, L, N, P, and Y can be introduced in eight manners: 4 each by rotation and reflection. Their symmetry group consists only of identity mapping.
• T and U can be introduced in 4 ways by rotation. Aligned with the gridlines, they have an axis of reflection. Their symmetry group consists of two elements, the identity and the reflection in a line that is parallel to the sides of the squares.
• V and W also can be introduced by rotation in 4 ways. At 45° to the gridlines, they have an axis of reflection symmetry. Their symmetry group has two elements, identity, and a diagonal reflection.
• Z can be introduced in 4 ways: 2 by turning, and 2 more by reflection. It has point symmetry, also called rotational symmetry of order 2. Its symmetry group consists of two elements, the identity, and the 180° rotation.
• I can be introduced in 2 ways and both by rotation. The two axes of reflection symmetry are both aligned with the gridlines. Its symmetry group consists of four components, the identity, two reflections, and the 180° turn. It is the dihedral gathering of order 2, too called the Klein four-group.
• X can be introduced in only one way. Aligned with the gridlines, it has four axes of reflection symmetry, and the diagonals, and rotational symmetry are of order four.

The chiral pentominoes are, L, N, P, Y, and Z; causing their reflections (F′, J, N′, Q, Y′, S) to obtain the number of one-sided pentominoes to 18. If rotations are also considered separate, then the pentominoes from the very first category would be eightfold, the ones from the following three categories (T, U, V, W, Z) would count fourfold, I counts twice, and X counts only one time. The output for 5×8 + 5×4 + 2 + 1 is 63 set pentominoes.

For the 2D figure, there are two more types:

• Being introduced in 2 ways by a rotation of 90°, with the two axes of reflection symmetry lined up with the diagonals. At least a heptomino is required for this type of symmetry.
• Being introduced in 2 ways, both are mirror images of each other, for example, a swastika. At least an octomino is required for this type of symmetry.

Three-dimensional Puzzles

If using cubes instead of squares for making a set of pentominoes, you can also try to solve many other puzzles. (Wooden cubes are sold at many craft stores, but try and make sure that they are of original sizes.) The first puzzle with these solid pentominoes should be able to place them into a 3x4x5 box.

From twelve pentominoes, ten can be called three-dimensional with all of the twelve pieces. Create the pentomino figures on a 2/1 scale, but only this time another dimension is added– their height should be three stories tall! Now, this technique is relatively easy as the pentominoes can be used in any way that works. Remember that there are two pentominoes that cannot be created in this way — the W and the X.

Example of Pentomino

Form a rectangular formation of pentominoes shapes with 5x12 shapes.

Solution

5×12 rectangular formation pentominoes  can be formed as:

Figure 4 – 5×12 Rectangle Formation

All images/mathematical drawings were created with GeoGebra.

Pentagonal Number Definition < Glossary Index > Percent Definition