Perpendicular Planes|Definition & Meaning

In geometry, a plane is a flat, two-dimensional surface that extends indefinitely in all directions. A plane is defined by three points that are not on the same line. The points can be connected to form a triangle, and the plane is the surface that contains the triangle. 

A plane can be perpendicular to another plane, meaning that the two planes intersect at a right angle. When this happens, the planes are said to be orthogonal to each other.

To visualize this, imagine two planes that intersect at a right angle. If you were to draw a line on one plane and extend it until it intersects the other plane, the line would be perpendicular to the second plane.

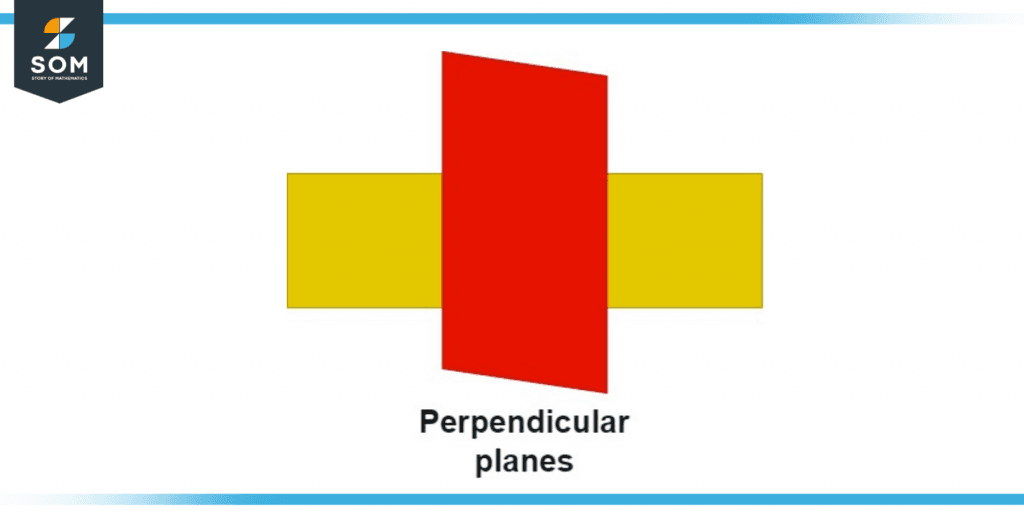
Figure 1 – Perpendicular planes

Perpendicular planes are often used in geometry to describe the orientation of objects in space. For example, if a plane is perpendicular to the ground, it is said to be “upright.” Similarly, if a plane is perpendicular to a wall, it is said to be “vertical.”

Understanding Perpendicular Planes Visually

If line l is also perpendicular to every one of the lines in plane A in which it intersects, then it can be said to be perpendicular to plane A.

Consider the image of a stick placed vertically on a plain and even surface. The stick is positioned in such a way that it is perpendicular to those lines that have been drawn on the table and that go through the location at which the stick is currently standing.

If plane B includes a line that also runs perpendicular to plane A, then plane B can be considered to be perpendicular to plane A.

The following figure shows the illustration of perpendicular planes.

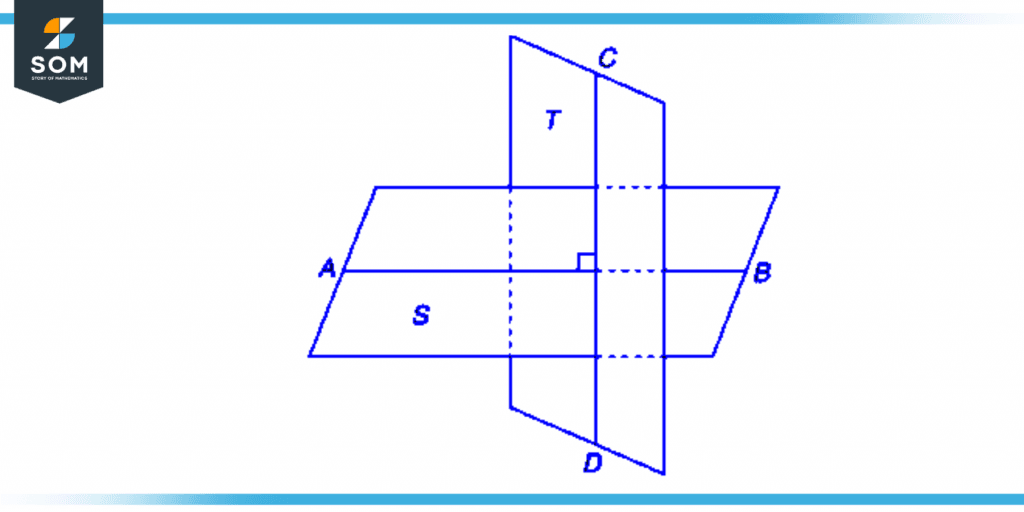
Figure 2 – Illustration of perpendicular planes

Planes are considered perpendicular to one another if their intersection is at a 90-degree angle. In geometry, one can encounter various distinct kinds of perpendicular planes, including the following

Planes That Cross One Another

Planes that cross are not parallel to one another, and their points of intersection are always aligned along a line. It is impossible for two planes to meet in much more than a line at any given point.

The diagram that follows illustrates how two planes, P and Q, meet at a single point on plane XY. As a result, line PQ is the line that connects to the Q plane through the XY plane. Intersecting planes can be seen in action in the form of the two walls that connect the rooms.

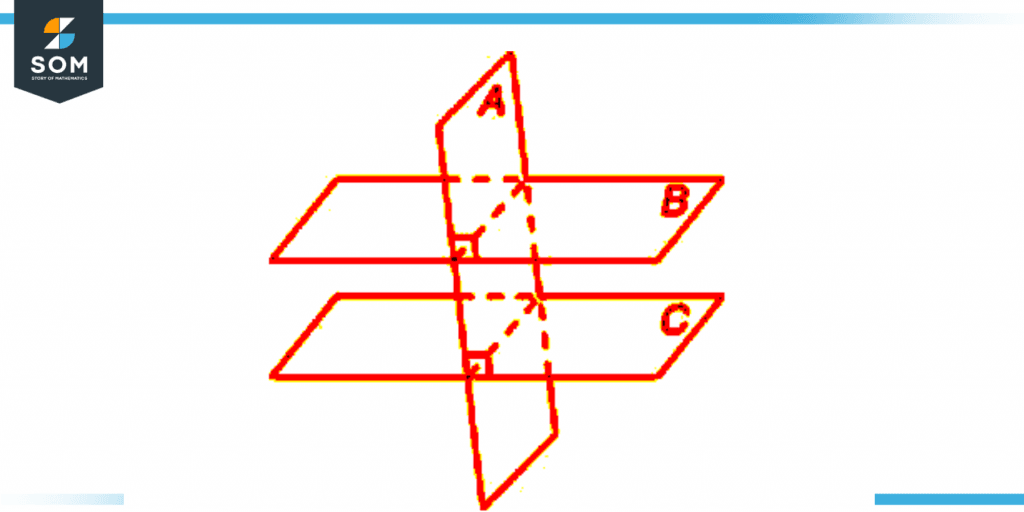
Figure 3 – Intersection of perpendicular planes

Orthogonal Lines or Planes

2 lines or indeed planes are said to be orthogonal if they intersect each other at right angles (90 degrees).

The lines AB and PQ in the illustration that follows are considered to be orthogonal because they intersect each other at a straight angle. In the context of geometry, the phrase “at right angles” is what the word “orthogonal” refers to.

Additionally, there are occasions when we refer to them as being “normal” to one another. To be very clear, the lines are not required to connect with one another at any point physically.

Even if they do not intersect, it is possible for two line segments to be considered orthogonal to one another. All that is required is that they are perpendicular to one another.

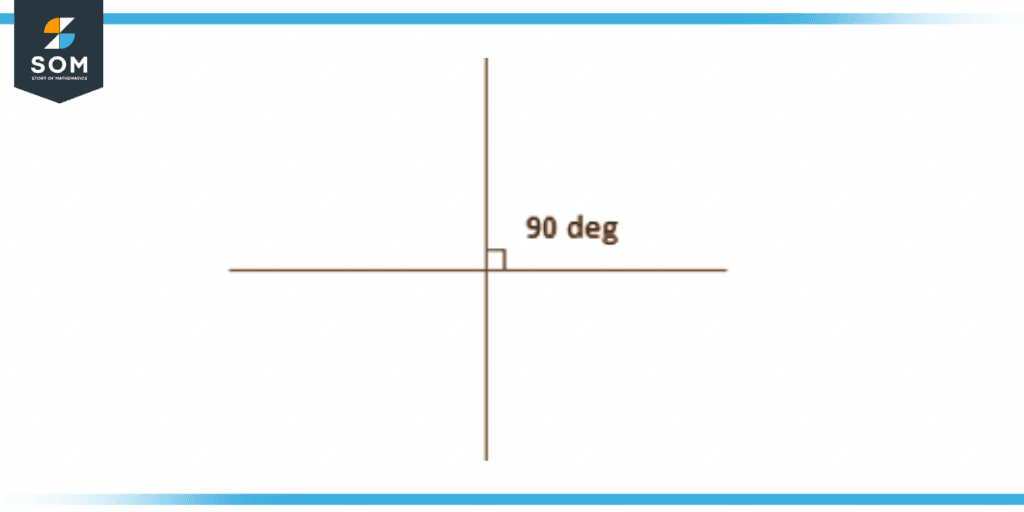
Figure 4 – Orthogonal line segment

Vertical Planes and Their Uses

A plane that is vertical is a plane that really is perpendicular to the surface of the ground. To put it another way, this is a plane that cuts across the horizontal plane at right angles.

It is possible to define a vertical plane in a three-dimensional coordinate system as a plane that is parallel to an x-y plane but perpendicular to the z-axis. This type of plane is known as a vertical plane.

For instance, the plane defined by the equation z = 0 is considered a vertical plane since it lies in a direction that is perpendicular to the x-y plane, which stands for the surface of the earth.

When creating a 3D model or drawing, vertical planes are frequently employed as the representation of walls, floors, as well as other vertical surfaces.

For the purpose of illustrating the wall of a building, vertical planes are frequently utilized in the field of architecture. In the field of engineering, the side of a bridge or even other structures are typically modeled with the use of vertical planes.

Perpendicular Plane Properties

When two planes are parallel to one another, but at right angles to one another, we say that the planes are perpendicular to one another. That the angle formed by the 2 planes is exactly ninety degrees is deduced from this. The following is a list of some properties that perpendicular planes have:

• Only if the normal vectors of the two planes are orthogonal can we say that the planes are indeed perpendicular to one another (i.e., perpendicular).Only when one normal vector’s projection on the other is zero do the planes become perpendicular.
• If the planes are perpendicular to one another, then every line which lies in one plane and therefore is perpendicular to the normal vector of such a plane will also be perpendicular to the corresponding plane. If the planes are not perpendicular to one another, then the planes are parallel to one another.
• If the planes were perpendicular to one another, any line that really is parallel towards the normal vector among one plane will also be parallel to a normal vector of the other plane if the planes were perpendicular to one.
• If two planes are parallel, then the distance between two points is equivalent to the length of a vector first from the point to the plane that is projected over onto the normal vector of a plane.

A Numerical Example of Perpendicular Planes

Example

Plane 1 is represented by the normal vector (2, 2, 3) while the second plane is represented by a normal vector(4, 4, 4). Show whether the two planes are perpendicular or not.

Solution

We know that if the dot product of the given vectors is not zero, the two planes are not perpendicular.

The dot product of two vectors results in 28 which is not equal to zero, so the given two planes are not perpendicular.

All mathematical drawings and images were created with GeoGebra.

Permutation Definition < Glossary Index > Peta Definition