Quintillion|Definition & Meaning

Figure 1 – Definition of Quintillion

What Is a Quintillion?

A number that encapsulates a huge amount is a quintillion. 1,000,000,000,000,000,000 is 1, followed by 18 zeros. Larger than a quadrillion but less than a sextillion, “quintillion” is a phrase used to represent a big sum.

The metric system does not recognize it as a standard unit of measurement, and it is often used to refer to astronomical distances, monetary sums, and vast volumes of data. 

Although the sheer size of a quintillion is difficult to grasp, it may be used to describe the number of stars in the observable universe, the total number of people using the Internet, or the amount of money required to address global issues. A quintillion is an astronomical number that, in essence, refers to an enormous amount.

What Is the Importance of Quintillion?

A quintillion is important because it is a term for an enormous sum. The importance of using such a word is that it might portray an enormity that is beyond the comprehension of the majority of people. It is useful to put astronomical distances, monetary amounts, and enormous amounts of data into perspective.

How To Write Quintillion in Scientific Notation?

The scientific notation for a quintillion is 1 x 10¹⁸. In scientific notation, a number is shown as the result of a power of 10 and a coefficient (1 in this example). The number of zeros in the starting number is represented by the power of 10. 

A quintillion is written as 1 x 10¹⁸ because there are 18 zeros in the definition of a quintillion. Large numbers may be expressed in a concise and condensed manner using this notation, which also facilitates simpler arithmetic operations.

How Much Is a Quintillion?

According to the American notation, a quintillion(10¹⁸) is equal to 1 followed by 18 zeros, but the British notation uses 1 followed by 30 zeros, i.e., 10$^{30}$.

Is Quintillion a Real Number?

Quintillions are actual numbers; therefore, yes. It is represented as a number in the American system of numeration by 1 and 18 zeros (10¹⁸) and by 1 and 30 zeros (10$^{30}$) in the British system.

Real numbers include both rational numbers (such as integers and fractions) and irrational numbers (such as $√2$ and $ π$).Although the term “quintillion” is used to represent exceedingly high amounts, it is nevertheless regarded as a real number in mathematics.

What Are the Types of Quintillion?

Depending on the numbering system employed, there are many variations of a quintillion. The most typical varieties are discussed below:

Short-Scale Quintillion

The most popular numbering scheme in the US and several other nations is the short-scale quintillion. A quintillion is defined as 10¹⁸, or a one followed by 18 zeros.

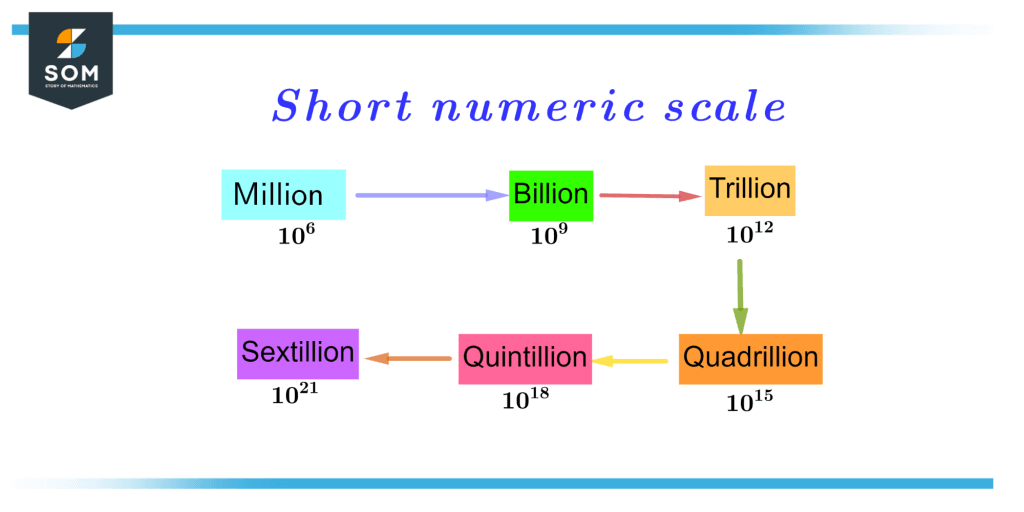
Figure 2 – Short Numeric Scale

Long Scale Quintillion

This numbering scheme is employed in France and Spain, among other nations. A quintillion is defined as 10$^{24}$, or a one followed by 24 zeros.

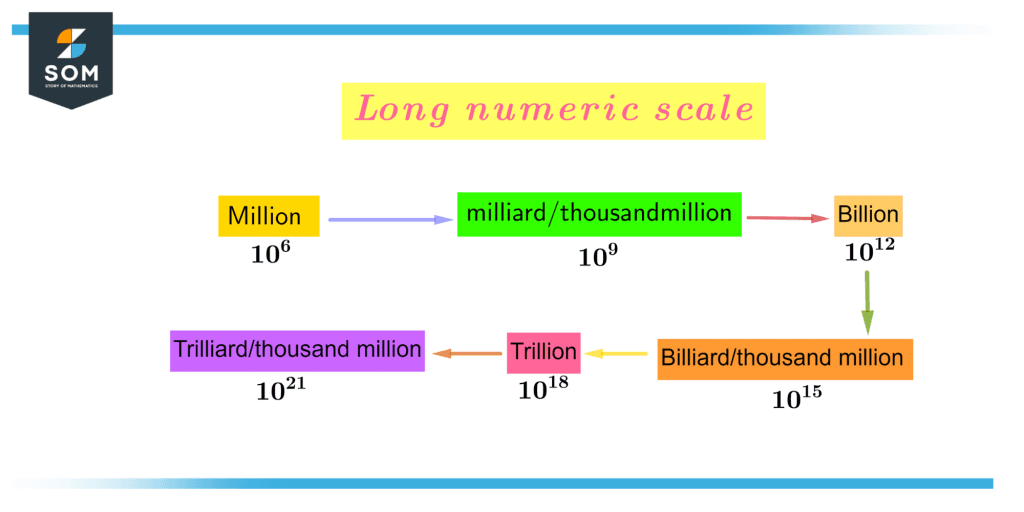
Figure 3 – Long Numeric Scale

In summary, the sort of quintillion used is dependent upon the numbering scheme utilized in a certain nation or area.

What Are the Advantages of Quintillion?

Here are some advantages of the quintillion:

1. Large Data Storage Capacity: Quintillion has the capability to store vast amounts of data, making it suitable for big data applications and complex data analysis.

2. High Processing Power: It can handle multiple tasks and processes simultaneously and quickly, allowing for efficient data processing and analysis.

3. Ability to Perform Complex Calculations: Quintillion is capable of performing complex mathematical operations, making it useful for scientific and research applications.

4. Efficient Data Management and Retrieval: It provides fast and organized data management and retrieval, making it easier to access and manipulate large data sets.

5. Improved Accuracy and Precision: With its powerful processing power and ability to handle complex calculations, quintillion can produce more accurate and precise results than traditional computing systems.

6. Supports Data-Intensive Applications and Research: Its high data storage and processing capacity make it ideal for applications and research that require large amounts of data, such as machine learning, artificial intelligence, and scientific simulations.

What Are the Limitations of Quintillion?

Here are some limitations of the quintillion:

1. High Cost of Ownership: Quintillion systems are often expensive, making it difficult for smaller organizations or individual users to purchase and maintain.

2. Complex Maintenance and Support Requirements: Quintillion requires specialized technical knowledge and resources for maintenance and support, which can be difficult to access and costly to acquire.

3. Limited Accessibility for Non-Technical Users: Due to its complex nature, quintillion can be difficult for non-technical users to understand and operate, which may limit its use to certain specialized applications.

4. Dependence on a Constant Power Supply: Quintillion systems require a constant power supply to function, making them vulnerable to power outages or other disruptions.

5. Vulnerability to Cyber Attacks: As with any computer system, quintillion is vulnerable to cyber attacks, which can lead to the loss or theft of sensitive data.

6. Limitations in Processing Certain Types of Data: Some data types, such as unstructured or real-time data, may be difficult for quintillion to process, requiring specialized hardware or software solutions.

Solved Examples of Quintillion in Mathematics

Example 1

What is 2 quintillions minus 10¹⁸?

Solution

The equation:

2 quintillion – 10¹⁸ = (2 x 10¹⁸) – 10¹⁸ = 10¹⁸ = 1 quintillion

Means:

2 quintillion is equal to 2 x 10¹⁸, where 10¹⁸ is equal to 1 quintillion.

Subtracting 10¹⁸  from 2 x 10¹⁸  results in 10¹⁸, which is equal to 1 quintillion.

So, the equation can be read as 2 quintillions minus 1 quintillion equals 1 quintillion.

Example 2

What is the result of 10¹⁸ multiplied by 5?

Solution

The equation 5 x 10¹⁸ = 5 quintillion expresses that the result of multiplying 5 and 10¹⁸ is equal to 5 quintillions.

Here:

10¹⁸ is a shorthand representation of 1 followed by 18 zeros, which is equal to 1 quintillion.

5 x 10¹⁸ means 5 times 1 quintillion.

Therefore, the equation 5 x 10¹⁸ = 5 quintillions mean that the result of 5 times 1 quintillion is equal to 5 quintillions.

Example 3

What is 2 quintillions divided by 10³?

Solution

The equation 2 quintillion divided by 10³ = 2 x 10¹⁵ = 2 x 10⁹ x 10⁶ = 2 x 10⁶ billion represents the calculation of the result of dividing 2 quintillions by 10³.

Here:

2 quintillion is equal to 2 x 10¹⁸, where 10¹⁸ is a shorthand representation of 1 followed by 18 zeros, which is equal to 1 quintillion.

10³ is a shorthand representation of 1 followed by 3 zeros, which is equal to 1000.

Dividing 2 x 10¹⁸ by 1000 results in 2 x 10¹⁵.

This can also be written as 2 x (10¹⁸ / 10³) = 2 x 10¹⁵.

Finally, 10¹⁵ is equal to 10⁶ billion.

So, the equation 2 quintillion divided by 10³ = 2 x 10¹⁵ = 2 x 10⁶ billion means that the result of dividing 2 quintillions by 1000 is equal to 2 x 10⁶ billion = 2 x 1,000,000 billion = 2,000,000 billion = 2 million billion.

All images were created with GeoGebra.