Regular Polygon|Definition & Meaning

Regular polygons include squares, equilateral triangles, and so on. Regular polygons have angles that are consistent with their sides. They are, therefore, equiangular.

Figure 1 below shows a regular polygon.

Figure 1 – Representation of a regular polygon.

A regular polygon is an n-sided polygon with sides that are all equal in length and then are symmetrically positioned around a common center (that is, the polygon is equiangular & equilateral).

Only some regular polygons remain “constructible” with the traditional Greek instruments of compass and straightedge.

As the name implies, “regular” within a regular polygon indicates a particular pattern that exists in the regular polygon.

Regular Polygon Properties

The following are the qualities of regular polygons:

• It has an equal number of sides.
• Its internal angles are all equal.
• Its external angles add up to 360°.

The prefix “regular” is always prefixed to a regular polygon. Regular polygons are convex, meaning all their internal angles are smaller than 180 degrees.

In basic terms, the regular polygon also has angles with the exact measurement at each vertex and all sides of the same length. In contrast, an irregular polygon does not have sides of the same height and angles of various measurements at each vertex.

Parts with Regular Polygons

Let us examine the parts of a single regular hexagon using a depiction of a regular polygon below:

• Sides: The sides are straight roads connecting two points.
• Vertices: A vertex is a point at which two sides meet.
• Angles on the inside and outside. An internal angle is formed by joining the edges of a polygon inside its enclosed surface.
• Diagonals

Figure 2 below shows portions of a regular hexagon

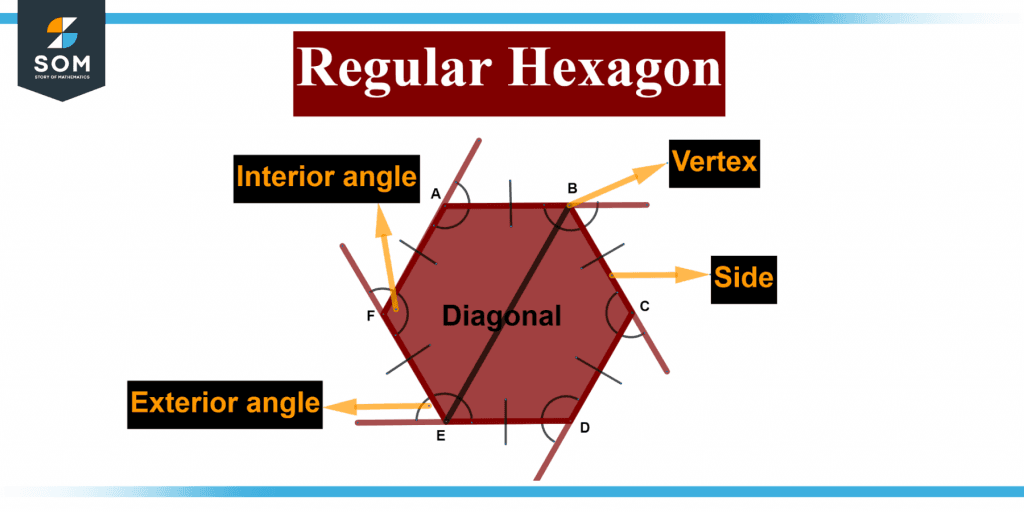
Figure 2 – A regular hexagon with its angles.

• (A), (B), (C), (D), (E), and (F) are the vertices.
• (AB), (BC), (CD), (DE), (EF), and (FA) are the equal sides.
• BE is defined as a regular polygon’s diagonal.
• The inner angles are identical to each other.
• The exterior angles are identical to one another.

Regular Polygon Perimeter

The regular polygon has equal sides. The perimeter of something like a polygon equals the total of its sides. A regular polygon having n sides has a perimeter equal to n times the side measure.

Regular Polygon Angles

As previously stated, there are two types of angles in the situation of either a regular polygon. They are as follows:

• Polygonal Exterior Angles
• Polygon Interior Angles

Regular Polygon Interior Angles

In a regular polygon, the internal angles are created between the adjacent edges inside the polygon and, thus, are equal to one another.

The total number of internal angles equals the total number of sides. The magnitude of the interior angle of either a regular polygon may be calculated using the following equation if the count of sides of something like the regular polygon is known:

The interior angle is equal to $\mathsf{\dfrac{180(n-2)}{n}}$, where n represents the number of sides.

For example, if a regular polygon’s side is 7 cm and it has five sides, the perimeter is 5 x 7 = 35 cm.

Regular Polygon Exterior Angles

A regular polygon’s exterior angles are formed by expanding one of the sides (anticlockwise and clockwise) and determining the angle between the extension and the next side.

The angle of a regular polygon stays unchanged, and the sum of the polygon’s outside angles equals 360°. If the number of sides is provided, the exterior angle of the regular polygon may be calculated using the following equation:

Exterior Angle = $\mathsf{\dfrac{360}{n}}$, where n represents the number of sides.

The Sum of a Regular Polygon’s Interior Angles

Consider an n-sided regular polygon. Because the edges of the regular polygon are equivalent, the total interior angles = (n – 2) x 180.

A regular polygon, for example, has five sides.

So, the total of the internal angles of a six-sided polygon is (n – 2) x 180 = (5 – 2) x 180 =540.

Number of Regular Polygon Triangles

If n is the number of edges of the regular polygon, then the amount of triangles generated by connecting the diagonals between one of the polygon’s corners is n – 2.

For example, if the number of sides is four, the amount of triangles produced is four.

(4 – 2) equals 2.

Figure 3 below shows triangles in a regular polygon.

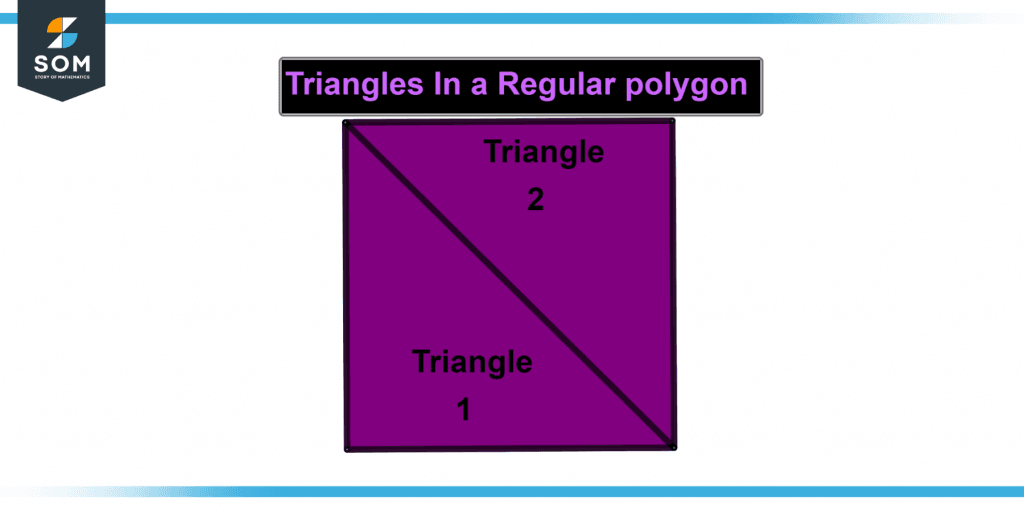
Figure 3 – Representation of triangles in a regular polygon.

Symmetry Lines of  the Regular Polygon

The vector or imaginary path that runs through the center of the form or item and splits it into equal halves is known as the line of symmetry. Because all the edges of a polygon are equal, then the number of planes of symmetry = n.

A square, for example, has four sides. As a result, the number of symmetry lines equals four.

Examples of Regular Polygon

Below are some examples of a regular polygon

Example 1

Adam is eager to determine the inside angle of a conventional hexagonal-shaped “STOP” signboard. Assist James in determining its internal angle.

Solution

Assume that the signboard is indeed a regular polygon. A signboard has a total of six sides. 

The formula gives the inner angle of a regular polygon. 

angle equals $\mathsf{180^\circ \times \dfrac{n-2}{n}}$.

Interior angle equals $\mathsf{180 \times \dfrac{6-2}{6}}$.

Interior angle equals $\mathsf{\dfrac{720}{6}}$ = 120 degrees.

As a result, each internal angle of a “STOP” board is 120 degrees.

Example 2

John is curious about the interior angle of a standard pentagonal-shaped signboard. Assist James in calculating the interior angle.

Solution

Assume the signboard is, in fact, a regular polygon. A signboard has six sides in total.

The formula gives a regular polygon’s inner angle.

The angle equals $\mathsf{180^\circ \times \dfrac{n-2}{n}}$. 

$\mathsf{180 \times \dfrac{5-2}{6}}$ is the interior angle, so the interior angle equals  $\mathsf{\dfrac{540}{6}}$ = 90 degrees

As a result, a board’s interior angle is 90 degrees.

Example 3

A student must find the perimeter of a regular polygon with 4 sides. Each side has a measurement of 10cm. Find the total perimeter of the regular polygon.

Solution

The regular polygon has 4 sides, each 10cm in length. We can use the perimeter formula to solve this problem. The formula is as follows:

Perimeter = Number of sides x Length of each side

We get:

4 x 10 = 40 cm

Which is the perimeter of the polygon.

All Images are made using GeoGebra.