Sum|Definition & Meaning

Figure 1 below shows the sum of two numbers.

Figure 1 – Representation of sum.

In mathematics, the phrase Sum refers to the outcome of adding numbers, objects, or things. This phrase appears regularly in our daily lives. For instance, when we buy a particular quantity of products, such as vegetables and fruits, we ask the vendor to calculate the total sum we must pay for the items. The whole amount is referred to as the sum in this context.

The sum is a method of grouping items together. The sum joins two binary numbers to create a new total. Terms like “altogether,” “put next to each other,” “how many in total,” “total,” and “sum” suggest that you must add multiple numbers together.

The Sum Notation

When we add numbers, we utilize the plus symbol (+). The sum is indeed the label given to the outcome of the addition. The total can be represented by the symbol (sigma). It is generally utilized when we add a list or a series of numbers.

Digit’s Sum

With full explanations, let’s look at how to get the sum of one-digit, two-digit, three-digit integers, and so on.

One-digit Number Sum

We may get two one-digit or single-digit integers in many combinations, such as 9, 8, 7, 6, 5, 4, 3, 2, 1.

Two-digit Number Sum

Determining the sum of the two-digit numbers occasionally necessitates carrying out the acquired result. The instructions below might help you find the sum of two-digit numbers.

Step 1: Fill in the blanks in the column with the supplied numbers, leaving enough space between them for easy comprehension.

Step 2: Combine the one-place digits and shift that carry (if any). Finally, it returns the sum of values in a single place.

Step 3: Add the previous step’s tens, place numbers and carry (if any), and transfer the burden. It returns the sum of tens of numbers.

Step 4: As a result, the last row numbers reflect the specified integers’ total.

Figure 2 below shows the sum of two-digit numbers.

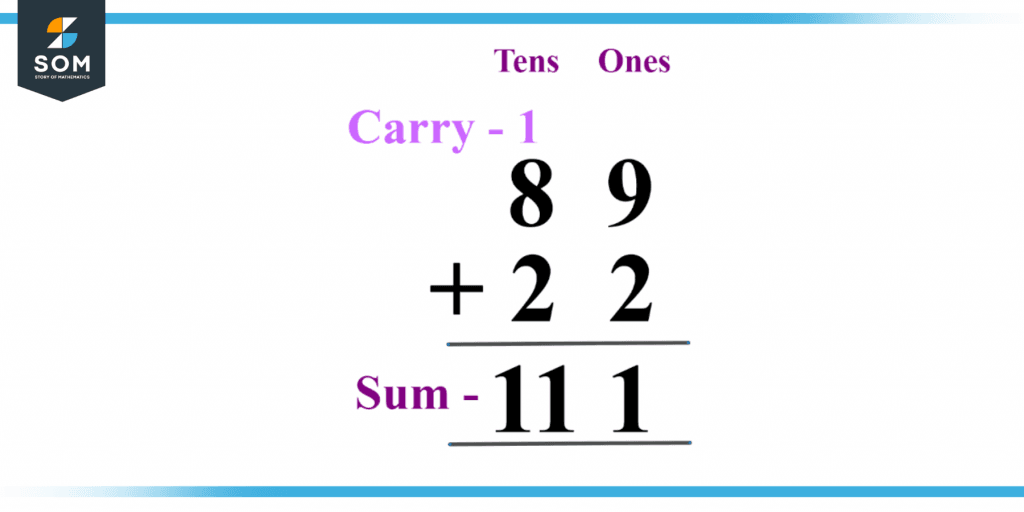
Figure 2 – Sum of two-digit numbers.

Sum of Three Digits

Now, proceed as follows to compute the sum of the 3-digit numbers:

Step 1: Use the given numbers to fill in the spaces in the column, allowing enough room between them for simple interpretation.

Step 2: Assemble the one-place numbers and send them (if any). Finally, it gives the total of the values all at once.

Step 3: Add the tens, place digits and carrying (if any) from the previous step, and transfer the responsibility. It returns the tens-of-tens total.

Step 4: Addition the numbers inside the location of the hundreds and carry the number from the previous step (if any). As a result, depending on the quantity, it returns the outcome in thousands, hundreds, or perhaps both.

Step 5: As a result, the last row numbers reflect the specified integers‘ total.

Figure 3 below shows the sum of three-digit numbers.

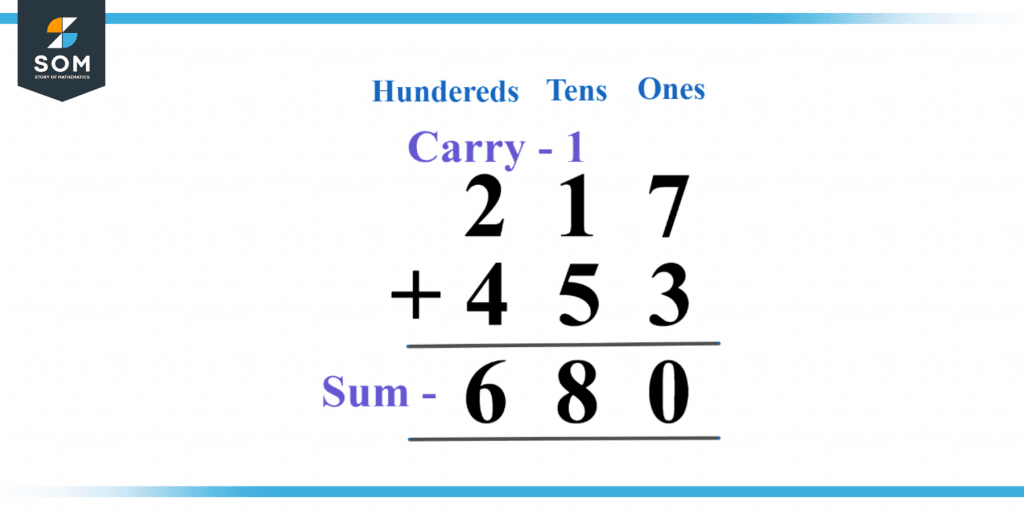
Figure 3 – Sum of three-digit numbers.

The Very First K Natural Digits Are Added Together

As we all know, a sum is a product of adding or combining a number sequence. As a result, we may compute the sum of a series’ first k positive integers.

The elementary k natural numbers are as follows: 1, 2, 3, 4,…., k

It is an AP with either a = 1 in the inaugural phrase or a = k in the last.

We understand that when we know the first and end terms of AP, the sum of k terms is given by:

S = $\mathsf{\left(\dfrac{k}{2}\right) (a + l)}$

= $\mathsf{\left(\dfrac{k}{2}\right)(1 + n)}$

= $\mathsf{n\left(\dfrac{k + 1}{2}\right)}$

As a result, the sum of the first k digits is $\mathsf{n\left(\dfrac{k + 1}{2}\right)}$.

The Formula for the Sum of the Odd Numbers

The odd number sequence is: 1, 3, 5, 7, 9, 11,…..

The following is an AP with a = 1 for the first term and a + d = 3 for the second term.

Difference in common = d = 3 – 1 = 2

The product of the initial k odd numbers seems to be:

S = $\mathsf{\left(\dfrac{k}{2}\right) [2a + (n – 1)d]}$

= $\mathsf{\left(\dfrac{k}{2}\right) [2(1) + (n – 1)(2)]}$

= $\mathsf{\left(\dfrac{k}{2}\right) [2 + 2n – 2]}$

= $\mathsf{\left(\dfrac{k}{2}\right)2n}$

= k$^{2}$

As a result, the sum of something like the odd numbers equation is k$^{2}$.

The Formula for the Sum of Even Numbers

The succession of even digits is as follows: 2, 4, 6, 8, 10,…..

That would be an AP with a = 2 for the first term and a + d = 4 for the second term.

Difference in common = d = 4 – 2 = 2

The product of the initial k digits is:

S = $\mathsf{\left(\dfrac{k}{2}\right) [2a + (k – 1)d]}$

=$\mathsf{\left(\dfrac{k}{2}\right) [2(2) + (k – 1)(2)]}$

= $\mathsf{\left(\dfrac{k}{2}\right) [4 + 2k – 2]}$

= $\mathsf{\left(\dfrac{k}{2}\right) [2(k + 1)]}$

= k(k + 1).

As a result, the formula for adding even numbers becomes k(k + 1).

Example of Sum in Solving Problems

John’s grandmother lives in the next village over.

To go to her grandmother’s house, she must cross a river.

She intends to bring 15 kg of sugarcane, 5 kg of jaggery, and 10 kg of tomatoes on the boat. On the ship, she may have a maximum load of 30 kg. Can she fit all of them into the ship?

Solution

We must determine the total mass of sugarcane, jaggery, and tomatoes.

Sugarcane weight = 15 kg

The weight of jaggery is 5 kg.

10 kg = tomato weight

The total mass of these items = 15 kg + 5 kg + 10 kg = 30 kg.

The boat’s carrying capacity is 30 kilograms.

All images are made using GeoGebra.