JUMP TO TOPIC
Weight|Definition & Meaning
Definition
Weight is defined as the gravitational force acting on the body in the downward direction. It measures how much gravity pulls the object according to its composed matter.
Figure 1 shows the weight of an object which depends upon how much matter the object is made of and the gravitational pull on it.
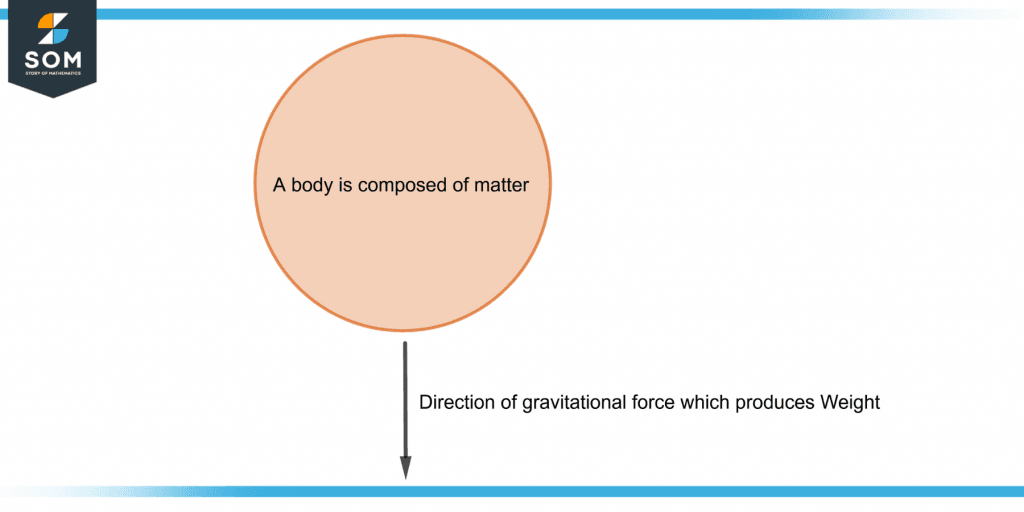
Figure 1 – Demonstration of Weight of an Object
Gravity
Weight cannot be understood without discussing gravity. It is the main reason we can stand and move on the Earth.
The attractive force between two bodies is called gravity. A bigger body has a greater force of attraction than a smaller body.
Newton’s law of gravitation, expressed mathematically, is:
F = G × $\mathsf{\dfrac{{m_1}{m_2}}{r^2}}$
Where,
m1 = mass of the first object
m2 = mass of the second object
r = distance from the centers of first and second objects
G = gravitational constant = 6.67 × 10-11 Nm2.kg-2
Figure 2 shows the parameters of the law of gravitation.
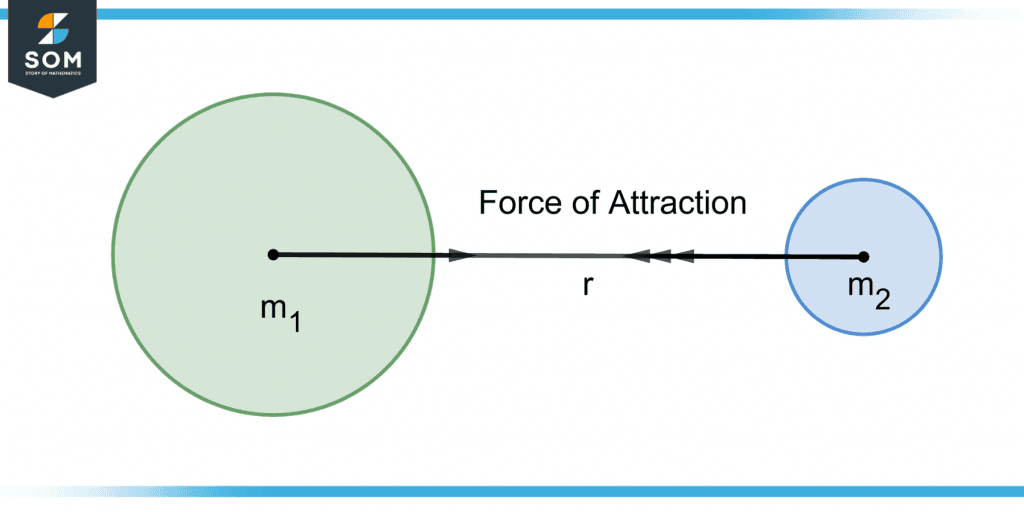
Figure 2 – Demonstration of the Law of Gravitation
Parameters in Weight’s Mathematical Formula
Force
Force is the external influence on a body to change its position. It changes the velocity of the object, causing the body to accelerate.
The direction of force is in the direction of acceleration produced, hence is a vector quantity.
If a body of mass m is applied with a force F, it produces acceleration a in the body. Mathematically, it can be expressed as
F = ma
This is also known as Newton’s second law of motion. Figure 3 shows its illustration.
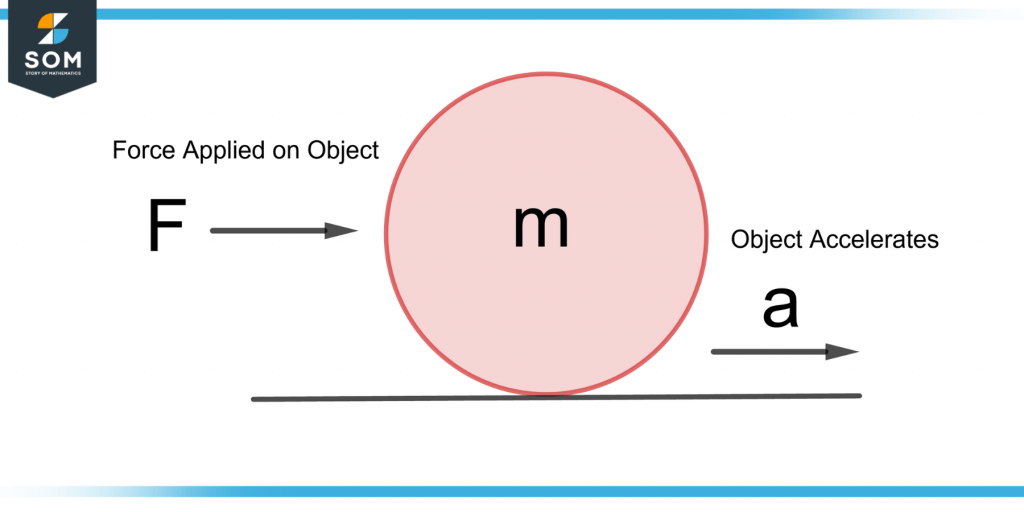
Figure 3 – Illustration of Newton’s Second Law of Motion
The SI unit of force is Newtons (N) which is equal to kilograms meters per second squared (kg.ms-2).
Mass
The mass is defined as the matter confined in an object. It is denoted by m, and its SI unit is kilograms (kg).
Gravitational Acceleration
Gravitational acceleration is the change in velocity caused by force due to gravity.
Planets have different gravitational fields, so the value of g is different for each. Table 1 shows the value of g for the nine planets.
| Name of Planets | g (m/s2) |
| Mercury | 3.7 |
| Venus | 8.87 |
| Earth | 9.8 |
| Mars | 3.69 |
| Jupiter | 23.12 |
| Saturn | 8.96 |
| Neptune | 11.0 |
| Uranus | 8.69 |
| Pluto | 0.66 |
Table 1
Mathematical Formula for Weight
According to Newton’s second law of motion:
F = ma
If the object falls freely on the ground, then
F = Fg , a = g
So the equation becomes
Fg = mg
As the gravitational force Fg is equal to the weight W of an object, the above equation can be written as:
W = mg
The weight depends upon two factors; the mass m and the gravitational acceleration g experienced by the object. It is demonstrated in figure 4.
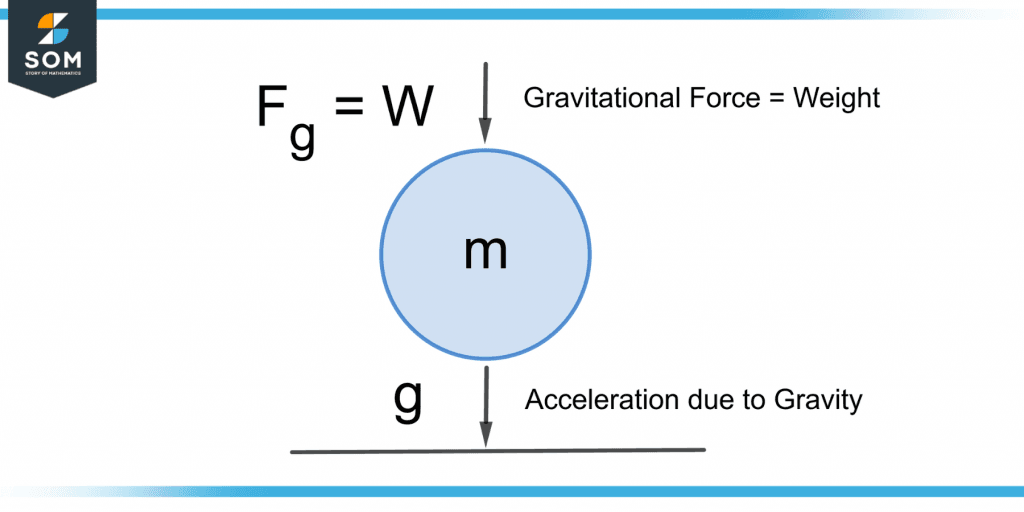
Figure 4 – Demonstration of “W = mg”
The unit of weight is the same as the force that is Newtons.
Difference Between Weight and Mass
Weight and mass are often perceived as similar but are two different quantities. The mass does not change, whereas weight changes when gravitational acceleration g changes.
For example, a car’s weight on Jupiter will be greater than its weight on Earth as the value of g is greater for Jupiter (23.12 ms-2) as compared to Earth (9.8 ms-2). But its mass will remain the same.
Weight is a vector quantity having a direction the same as the direction of g, whereas mass is scalar.
Weighing Scales
People often confuse weight with mass, as the scales which measure mass are called “weighing scales.” The term “weight” is more common among people than “mass.”
These scales measure the force exerted on them due to gravity which is usually the same everywhere as we live on the planet Earth.
The units in which weight or what should be called mass is measured are as follows:
Metric Units
The scales that weigh mass are measured in kilograms (kg), grams(g), and tonne(t). They are related as follows:
1 kg = 1000 g
1 t = 1000 kg = 1,000,000 g
US Units
The US has separate units measuring mass in pounds, ounces, and tons. They are related as follows:
1 pound = 16 ounces
1 ton = 2000 pounds = 32,000 ounces
Apparent Weight
So far, we have discussed the real weight W. Apparent weight is defined as the upward reaction of the gravitational force acting on an object. It is also known as tension and is denoted by T.
Apparent weight changes with the object’s motion, whereas the real weight remains the same.
Consider a person standing in an elevator on a weighing scale. Four cases of the object’s motion are discussed:
Case 1
Consider the person and the elevator at rest or the lift moving with uniform velocity. In this case, acceleration will be 0. The net force acting on the body will be
Fnet = T – W
ma = T – W
As a = 0, so
0 = T – W
T = W
In this case, the apparent weight will be equal to the real weight.
Case 2
If the elevator moves in an upward direction with acceleration a, the net force on the body will be
Fnet = T – W
ma = T – W
T = W + ma
The apparent weight is now the real weight of the object plus the upward force acting on it. Hence the apparent weight is more than the real weight.
Case 3
If the elevator goes down with acceleration a, the apparent weight of the person decreases by ma as the signs of W and T change.
Fnet = W – T
ma = W – T
T = W – ma
Case 4
If the elevator free falls, its acceleration equals the gravitational acceleration. The Fnet will be the same as for the elevator going downwards, so
Fnet = W – T
ma = mg – T
Substituting a = g,
mg = mg – T
Subtracting mg on both sides, so
T = 0
Figure 5 shows the four cases of apparent weight.
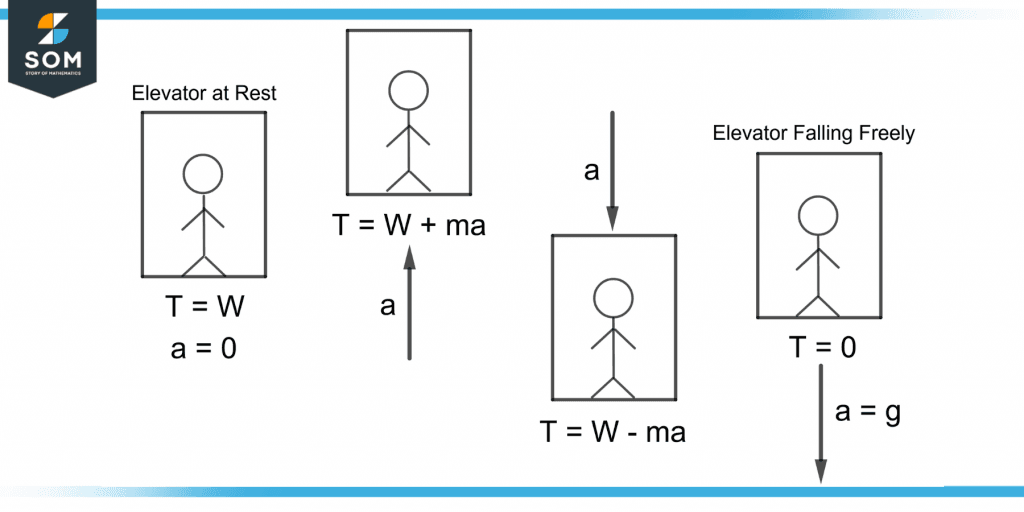
Figure 5 – Demonstration of Four Cases of Apparent Weight
An Example of Calculating an Object’s Weight
An object of mass 20 kg is placed on the Earth and the planet Mars. Calculate its weight on the planets Earth and Mars.
Solution
The equation for weight is:
W = mg
Here, m = 20 kg. The value of g is 9.8 ms-2 on planet Earth. Its weight on the Earth will be:
W = (20)(9.8)
W = 196 N
The value of g on Mars from Table 1 is 3.69 ms-2. Its weight on Mars will be:
W = (20)(3.69)
W = 73.8 N
All the images are created using GeoGebra.
