Hippocrates of Chios – History, biography and accomplishments

Hippocrates of Chios

Hippocrates of Chios was a Greek mathematician, geometer and astronomer. He grew up on the island of Chios, which is the fifth largest of the Greek islands and is much closer to Turkey than to Greece, and later moved to Athens.

In Athens, he taught geometry, wrote a systematic geometry textbook called the Elements, made contributions to the geometry of circles, and proposed astronomical theories about the nature of comets.

Hippocrates’ timeline, birth and death

Early life

Hippocrates was born around 470 BC on the Greek island of Chios. Nothing is known about Hippocrates’ family. He grew up on Chios and is thought to have studied under the geometer and astronomer Oenopides of Chios.

He was influenced by Pythagorean thought, which was popular on the nearby island of Samos.

Adult life

Hippocrates began his career as a merchant. At one point he suffered a financial loss: either being cheated by customs officials (according to Aristotle) or robbed by pirates (according to the 5th-century historian John Philoponus). He travelled to Athens to seek justice. This was unsuccessful, and there is evidence that the Athenians laughed at him for his foolishness. The attempt required him to stay in Athens for a long time, so he began attending lectures in philosophy and geometry, and started his own geometry school to provide himself with an income. He settled in Athens and taught geometry, and made novel contributions to geometry and astronomy.

He died around 410 BC in Athens.

He should not be confused with Hippocrates of Kos, the doctor and originator of the Hippocratic Oath, who lived at the same time.

Hippocrates’ contributions and accomplishments

Elements

Hippocrates was the first person to compile a systematic geometry textbook reflecting the current state of geometrical knowledge. His book was called the Elements and is likely to have been the foundation for Euclid’s later and better-known Elements, which remained the standard geometry textbook right up until the modern era.

Hippocrates’ Elements gave mathematicians across the ancient world a systematic foundation and common language for discussing and building on their knowledge, which boosted progress in mathematics. For example, he is thought to have originated the convention of using letters to refer to geometric points, as in “the triangle ABC”.

His textbook is no longer extant, but an excerpt from it is quoted in the work of Simplicius of Cilicia, a 5th-century Neoplatonist philosopher. Hippocrates’ Elements provided a foundation for other mathematicians, including Euclid, to write their own textbooks, refining and improving the structure and terminology introduced by Hippocrates. Many of the principles in Euclid’s textbook are likely to have also appeared in Hippocrates’ version.

Hippocrates and squaring the circle

During his time in Athens, Hippocrates worked on the problem of squaring the circle, one of the classic geometrical problems of antiquity along with doubling the cube and trisecting the angle. The aim of squaring the circle was to construct, using only compass and straightedge, a square whose area can be proved to be equal to the area of a given circle.

(Many centuries later, Ferdinand von Lindemann proved that π, the ratio of a circle’s area to its diameter, is transcendental, meaning it cannot be expressed as a root of a polynomial equation with integer coefficients. Hence, von Lindemann proved that squaring the circle is impossible.)

The Lune of Hippocrates

While working on the problem of squaring the circle, Hippocrates determined the area of a lune (a crescent shape bounded by two intersecting circles) bounded by a semicircle and a quarter-circle. In the image below, the shaded lune is bounded on the lower side (F) by a quarter of the circle with diameter AC, and on the upper side (E) by half of the circle with diameter AB, where AB is a chord of the larger circle spanning a right-angle (AOB).

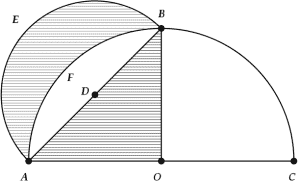
Image credit: Wikipedia, Lune.svg, public domain

Hippocrates proved that the area of the shaded lune was the same as the area of the shaded triangle AOB. He saw this as a step towards squaring the circle, since he had determined the area of a shape bounded by arcs of circles and had constructed a shape of equal area bounded by straight lines.

The mathematical historian Sir Thomas Little Heath observed in 1931 that Hippocrates’ proof entailed the important discovery that the area of a circle is proportional to its diameter, although it is unknown whether Hippocrates himself realized this implication. However, the French mathematician Paul Tannery argued that Hippocrates’ solution was actually based on the theorem that the areas of circles are in the same ratio as the squares of their bases or diameters, and that this theorem was known and taken for granted by Hippocrates.

The lune described above became known as the Lune of Hippocrates. Hippocrates found two other lunes that could also be squared, i.e. a square of the same area as the lune could be constructed using a compass and straightedge. It was not until the 19th century that any other squarable lunes were discovered, with two more being identified by Clausen, and in the 20th century Tschebatorew and Dorodnow proved that those five were the only squarable lunes.

Doubling the cube

Hippocrates’ discoveries also include a step towards a method for doubling the cube: given a line segment representing the edge of a cube, using compass and straightedge to construct a line segment for the edge of a cube with twice the volume of the first. Like squaring the circle, this was one of the classical problems that intrigued ancient mathematicians, but was proven impossible many centuries later.

Doubling the cube is equivalent to finding the cube root of 2: starting with a line segment of unit length, which can form an edge of a cube of unit volume, the problem requires constructing an edge of a cube of volume 2, which would be a line segment of length ³√2.

Hippocrates discovered an intermediate step toward doubling the cube: finding two “mean proportionals” x and y, geometrically evenly spaced between the original side length, a, and its double, 2a, such that a:x = x:y = y:2a.

Hippocrates knew that the problem of doubling a square could be solved by finding one mean proportional between the side length a and 2a, so he generalized the concept to the three-dimensional problem. He may also have been inspired by insights in number theory. Plato cites the proposition, later proved by Euclid, that there is one mean proportional between two square numbers, and two between two cube numbers. Hippocrates may have been aware of this proposition via his Pythagorean background, and applied it to geometry.

Reduction

Hippocrates is thought to have introduced the general approach of reducing a problem to a simpler or a more general one. His approach to doubling the cube is an example, reducing the three-dimensional problem of doubling the cube to a one-dimensional problem of finding two lengths.

The 5th-century philosopher Proclus Lycaeus credited Hippocrates with being the first to apply the technique of reduction to geometric problems, which he described as “a transition from one problem or theorem to another, which being known or solved, that which is propounded is also manifest.”

The technique of reductio ad absurdum or proof by contradiction, still frequently used by mathematicians today, is a related concept. It can be used, for example, to prove that there is no smallest rational number (if there were, it could be divided by 2 to get a smaller number that is still rational, so the original number cannot have been the smallest rational number), or to prove that the square root of 2 is irrational (if it were rational, it could be expressed as an irreducible fraction p/q for some integers p and q; squaring both sides, p²/q² = 2, so p² = 2q², which means p² is even; therefore p is even, as squares of odd integers cannot be even; therefore p = 2k for some other integer k; therefore p² = 2q²= (2k)² = 4k²; therefore q² = 2k²; therefore q² and hence q is also even; therefore p and q have a common factor after all, 2, and p/q was not an irreducible fraction.)

Astronomy

Hippocrates was also a practitioner of astronomy, which he probably would have learned while still living on Chios, as it was studied there. Hippocrates’ tutor Oenopides had previously traveled to Egypt and studied both geometry and astronomy under the Egyptian priests.

Contemporary astronomers believed that all comets seen from Earth were actually a single body – a planet with a long and irregular orbit. This planet was thought to have a low elevation above the horizon, like the planet Mercury, because, like Mercury, comets cannot be seen when the sun is risen, but can only be seen when they are low on the horizon during the time before sunrise or after sunset. Hippocrates endorsed this theory of a single comet, according to Aristotle, who attributed it to “the school of Hippocrates”, and wrote that Hippocrates also tried to account for the tail of the comet by proposing that it was an optical illusion caused by moisture.

Hippocrates and his contemporaries believed that vision worked by light rays originating from our eyes and traveling to the object seen, rather than the other way around. In his account, moisture near the comet, attracted by the comet as it traveled near the sun, refracted the light rays from our eyes as they approached the comet, deflecting them toward the sun. He believed that this moisture was plentiful in the north but scarce in the area between the tropics, being unaware of how distant the sun and planets are from the earth but believing them to travel through its atmosphere.

According to Olympiodorus and Alexander, Hippocrates had a similar theory about the appearance of the Milky Way: that it was, in Aristotle’s words, “a deflection of our sight toward the sun as is the case with the comet.” In the case of the Milky Way, he believed that the moisture causing the refractive illusion came from the stars. Aristotle, in his Meteorologica, critiqued this theory and refuted it.