Law of Detachment – Explanation and Examples

The law of detachment states that if the antecedent of a true conditional statement is true, then the consequence of the conditional statement is also true.

This law regards the truth value of conditional statements.

Before moving on with this section, make sure to review conditional statements and the law of syllogism.

This section covers:

• What is the Law of Detachment?
• Law of Detachment Examples

What Is the Law of Detachment?

The law of detachment states that if a conditional statement is true and its antecedent is true, then the consequence must also be true.

Recall that the antecedent is what follows the word “if” in a conditional statement. A consequence is what follows the word “then.”

Note that this does not work the other way unless the statement is biconditional. That is, if the consequence is true, it is impossible to conclude whether the antecedent is true or false.

Similarly, if the antecedent is false, that is not enough information to conclude that the consequence is true.

In mathematical logic, this fact is:

If “$P \rightarrow Q$ is true and $P$ is true, then $Q$ is true.

Law of Detachment Examples

There are endless examples both in mathematics and beyond of the law of detachment.

One example is a coffee shop that gives a free drink to every 25th customer. As a conditional statement, this is “If someone is the 25th customer, then they get a free drink.”

Thus, if you are the 25th customer, you know you will get a free drink. Likewise, if your friend is the 25th customer, you know he will get a free drink.

Someone could get a free drink in another way. For example, they could have a coupon. Therefore, knowing someone got a free drink is not enough to conclude that they were the 25th customer. Likewise, if someone is not the 25th customer, that is not enough information to know that they did not get a free drink.

Examples

This section covers common examples of problems involving the law of detachment and their step-by-step solutions.

Example 1

Suppose the following statement is true:

For every convex quadrilateral, the interior angles add up to $360^{\circ}$.

Which of the following figures can you conclude that the interior angles total $360^{\circ}$?

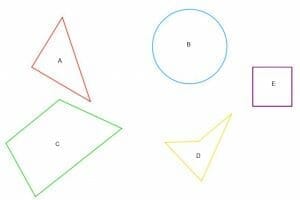
Solution

If a figure satisfies the antecedent, it must also satisfy the consequence.

The first two figures, A and B, are not quadrilaterals. Therefore, it is not possible to conclude that the sum of the interior angles to $360^{\circ}$ from the statement.

Figures C, D, and E are all quadrilaterals. Figure D, however, is not convex. Therefore, there is not enough information to make a conclusion.

Since figures C and E are both convex quadrilaterals, the law of detachment says the consequence of the conditional statement is true. Therefore, the total of their interior angles is $360^{\circ}$.

Example 2

Suppose the following statement is true:

If it rains, then I will bring an umbrella.

Now consider separately that the following are also true. What can be concluded?

A. It is raining.

B. I will bring an umbrella.

Solution

Consider situation A first.

Since the antecedent of the true conditional statement is true, the consequence must also be true. Therefore, these two statements are enough to conclude that I will bring an umbrella.

In the second case, the statements “if it rains, then I will bring an umbrella” and “I will bring an umbrella” are both true.

In this case, the statement and its consequence are true. Unfortunately, this is not enough information to conclude that it is raining. In fact, no conclusions can be drawn from this information alone.

Example 3

Suppose the following statement is true:

“It is a gizmo if and only if it is a widget.”

Now consider separately that the following are also true. What can be concluded?

A. It is a gizmo.

B. It is a widget.

Solution

Note that in this case, the conditional statement is a biconditional statement. Recall that a biconditional statement is one for which $P \rightarrow Q$ and $Q \rightarrow P$ are both true.

Now, first, assume A.

In this case, the biconditional statement being true means that the statement “if it is a gizmo, then it is a widget” is true. Since “it is a gizmo” is the antecedent, and it is true, it is possible to conclude the consequence. Therefore, conclude that it is a widget.

Now, consider case B. Since the biconditional statement is true, the statement “if it is a widget, then it is a gizmo” is also true.

Since the antecedent of this true statement is true, the consequence must also be true. Therefore, it is possible to conclude that it is a gizmo.

Example 4

Suppose that the following two statements are both true.

• “If it is a cat, then it is a feline.”
• “If it is a feline, then it is a mammal.”

Then, suppose separately that each of the following are true.

A. It is a mammal.

B. The animal is a feline.

C. It is a cat.

Solution

First, for A, assume that the three statements, “if it is a cat, then it is a feline,” “if it is a feline, then it is a mammal,” and “it is a mammal,” are all true. In this case, “it is a mammal” is the consequence of the second statement. Since it is not an antecedent, there is nothing to conclude.

For B, assume the statements “if it is a cat, then it is a feline,” “if it is a feline, then it is a mammal,” and “it is a feline” are true.

In this case, the first statement is extraneous. “It is a feline” is the antecedent of the second conditional statement. Since it is true and so is the antecedent, the consequence must also be true. Therefore, it is a mammal.

Finally, assume “if it is a cat, then it is a feline,” “if it is a feline, then it is a mammal,” and “it is a cat” are all true. Combining the first statement, “if it is a cat, then it is a feline,” with “it is a cat” is enough to conclude that “it is a feline is true.”

That is not all, however. In this case, it is also important to remember the law of syllogism. This states that if $P \rightarrow Q$ and $Q \rightarrow R$ are both true, then $P \rightarrow R$. Here, since “if it is a cat, then it is a feline” and “if it is a feline, then it is a mammal” are both true, “if it is a cat, then it is a mammal must be true.”

Therefore, since “it is a cat” is true, the consequence “it is a mammal” must also be true.

Example 5

Use the law of syllogism and the law of detachment to draw conclusions if all of the following are true:

1. “If Dante fails his test, he will fail his class.”

2. “If Adventures in Space is on television, Dante will stay up to watch television.”

3. “Adventures in Space is on television.”

4. “If Dante fails his class, he will get in trouble with his parents.”

5. “If Dante stays up to watch television, then he will fail his test.”

Solution

The first step, in this case, is to put the statements in a more logical order so that it is easier to apply the law of syllogism.

Statement 3 is the only one that is not a conditional statement, so it should go at the end.

Statement 2 states that “if Adventures in Space is on television, Dante will stay up to watch television.” Since “Adventures in Space is on television” is not the consequence of any other statement, this one is likely first.

In fact, starting at statement 2, it is possible to make a string of statements where the consequence of one is the antecedent of the next.

Statement 2 $\rightarrow$ statement 5 $\rightarrow$ statement 1 $\rightarrow$ statement 4. Then, the end is statement 3.

Using the law of syllogism with the first four statements yields “if Adventures in Space is on television, he (Dante) will get in trouble with his parents.” Since each of the intermediary statements is true, this statement is true.

The antecedent of this statement, “Adventures in Space is on television,” is also true. Therefore, by the law of detachment, the conclusion of the statement, “Dante will get in trouble with his parents,” must also be true.

Practice Problems

1. Suppose the following statement is true:
“If a prime number is greater than two, then it is odd.”
Which of the following are odd based on this statement?
A. 2
B. 3
C. 5
D. 9
E. 10

2. Suppose the following is a true statement:
“If it is October, then it is fall.”
What can be concluded from the following?
A. It is October 8
B. The date is September 29
C. It is fall

3. Let these statements be true:
“If it is a carrot, it is a vegetable.”
“It is a cabbage.”
What can be concluded?

4. Suppose these statements are true:
“$P \rightarrow Q$.”
“$\neg Q$.”
What can be concluded?

5. Suppose these statements are true:
“If it is cheese, it contains dairy.”
“If it contains dairy, Sonja cannot eat it.”
“It is cheese.”
What can be concluded?

Answer Key

1. Only the numbers 3 and 5 because the number 9 is odd, but the statement doesn’t give enough information to conclude that.
2. A means it is fall. Nothing can be concluded from B and C.
3. Nothing can be concluded.
4. By contrapositive, concluded $\neg P$.
5. By the law of detachment, it is dairy. Because of this and the law of syllogism, Sonja cannot eat it.

Images/mathematical drawings are created with GeoGebra.