JUMP TO TOPIC
Acid-Base Calculator + Online Solver With Free Easy Steps
The online Acid-Base Calculator helps you determine the pH value of weak acids and bases.
The Acid-Base Calculator is beneficial when handling chemicals because scientists need precise value concentrations while working in laboratories or research facilities.

What Is an Acid-Base Calculator?
An Acid-Base Calculator is a free online calculator for calculating the pH value of weak acids and bases.
The Acid-Base Calculator needs two inputs: it asks for the molarity and the acid’s or base’s name. You need to press the “Submit” button to get the results.
How To Use an Acid-Base Calculator?
You can utilize the Acid-Base Calculator by inputting the molarity and the acid or base’s name into the designated boxes.
The step-by-step instruction on using the Acid-Base Calculator are given below:
Step 1
Firstly, you may enter the molarity of your Acid or base.
Step 2
Then, enter the name of your Acid or base in your Acid-Base Calculator.
Step 3
Once you have inputted the molarity and acid name, click the “Submit” button on your Acid-Base Calculator. The results of the Acid-Base Calculator are shown in a new window.
How Does an Acid-Base Calculator Work?
An Acid-Base Calculator works by putting in the value and the name, which then provides you with the pH value. The online Acid-Base Calculator tool accelerates and streamlines the calculation, quickly displaying the equilibrium constants and pH values.
What Are Weak Acids?
Weak acids are the acids that partially split into their ions in water or an aqueous solution. In contrast, a strong acid completely dissociates into its ions in water. While the conjugate Acid of a weak base is also a weak acid, the conjugate base of a weak acid is also a weak base.
Below are some examples on how weak acids are represented:
$H_{2}S0_{3}$ – Sulphurous Acid
$HC0_{2}H$ – Methanoic Acid
$HNO_{2}$ – Nitrous Acid
Here are some examples of weak acids:
Formic Acids
Formic Acid, commonly known as methanoic acid, is one of the simplest carboxylic acids. This substance’s chemical name is HCOOH. It is an actual example of a weak acid and is known to occur in the bodies of ants.
Acetic Acids
The chemical name for acetic acid, commonly referred to as ethanoic acid, is $CH_{3}COOH$. It is well recognized as the substance that makes vinegar, a 4–7% acetic acid solution in water, work. Because it only partially separates into its constituent ions when acetic Acid is dissolved in water, acetic acid is a weak acid.
What Are Weak Bases?
Weak bases are basic substances that do not completely separate into their constituent ions when dissolved in liquids. As a result, when a weak base is dissolved in a solution, some of it dissociates into hydroxide anions and the appropriate conjugate acid while the remainder stays undissociated.
Here is the following chemical reaction of a weak base:
\[ B+H_{2}O \rightleftharpoons BH^{+} + OH^{-} \]
According to the Bronsted-Lowry definition, a base is a substance that accepts hydrogen ions or protons. Weak bases are defined as chemical compounds in which the addition of protons or hydrogen ions is still pending.
Arrhenius’s theory defines it as substances that release hydroxide ions in the aqueous solution.
Here is an example of a weak base:
Ammonia
Ammonia is a weak base and has the formula $NH_{3}$. Ammonia exists at average temperatures and pressures as a colorless gas. It is well known that the scent of this gas defines it.
What Is Ka?
Acid disassociation (Ka) is the factor that determines whether an acid is strong or weak. As Ka rises, the Acid disassociates more. Therefore, Strong acids may disassociate more in water. The strength of an acid in a solution is numerically represented by this equilibrium constant.
On the other hand, a weak acid has a lower propensity to ionize and release a hydrogen ion, leading to a less acidic solution.
Ka is often stated in $\frac{mol}{L}$ units.
It is possible to determine the equilibrium location using Ka. The production of disassociation is favored when the Ka is high. An acid that hasn’t been dissolved takes precedes when Ka is low.
Ka can be used to determine the potency of an acid. The Acid is highly dissociated and potent if Ka is high (and pKa is low).
You can calculate Ka by using the following formula:
\[ K_{a}=\frac{[A^{-}][H^{+}]}{[HA]} \]
What Is pKa?
pKa is the base-10 negative logarithm of a solution’s acid dissociation constant or Ka, and pKa is represented by:
pKa = -log{10}Ka
The Acid is more potent, and the lower the pKa value. Lactic Acid, for example, has a pKa of 3.8, and Acetic Acid has a pKa of 4.8.
It is utilized because pKa describes acid dissociation using small decimal integers. Ka values can be used to gain the same information; however, these are often minimal quantities presented in scientific notation that are difficult to interpret for most people.
Relationship Between Ka and pKa
The relationship between Ka and pka is shown by the equation of acid dissociation in an aqueous solution, as shown below:
\[ HA + H_{2}O\leftrightharpoons A^{-} + H_{3}O^{-} \]
Where $H^{+}$ is a hydrogen ion that combines with a water molecule to generate $H_{3}O$ and HA is an acid that disassociates into its conjugate base A-.
Chemical species HA, A, and $H_{3}O$ are considered in equilibrium when their concentrations do not change over time. It is customary to express the equilibrium concentrations, denoted by [HA], [A], and $[H_{3}O]$, as a fraction of the disassociation constant Ka.
\[ Ka = \frac{[A^{-}][H^{3}O]}{[HA][H_{2}O]} \]
In most cases, water doesn’t dramatically alter in concentration while the Acid reacts with it (unless in the most concentrated aqueous solutions of an acid)
It can therefore be overlooked and viewed as a constant.
\[ HA\leftrightharpoons A^{-}+H^{+} \]
\[ Ka = [\frac{[A-][H+]}{[HA]} \]
The response and definition can then be expressed more clearly.
pKa = -log{10}Ka
For many applications, it is more convenient to talk about the logarithmic constant, pKa. The following is the link between Ka, pKa, and acid strength: the weaker the acid, the lower the Ka value, and the higher the pKa value.
Solved Examples
The Acid-Base Calculator is used to find the $pH$ value of a weak acid. Here are some examples solved by an Acid-Base Calculator.
Example 1
A high school student is provided an Acetic Acid sample with a molarity of 0.05 \ M. The student needs to calculate the pH value of this weak Acid. Using the Acid-Base Calculator, find the pH value of the Acid.
Solution
Using the Acid-Base Calculator, we can easily find the pH value of the Acid. First, we input our molarity value, 0.05 \ M. Next, we enter the type of weak Acid we have, Acetic Acid in our case. Finally, after entering all the inputs, we click the “Submit” button on the Calculator.
The Acid-Base Calculator displays the pH value along with additional acid-base information. The Calculator also shows a graph.
The results from the Acid-Base Calculator are shown below:
Input Interpretation:
0.05 M acetic acid
Result:
3.03
Acid-Base information:
Ka = 0.0000175
pKa = 4.76
pH = 3.03
\[ [H_{3}O^{+}] = 9.28\times 10^{-4} \ \frac{mol}{L} \ (moles \ per \ liter) \]
pOH = 11.0
\[ OH^{-} = 1.08\times 10^{-11} \ \frac{mol}{L} \ (moles \ per \ liter) \]
% ionization = 1.86%
pH vs concentration plot:
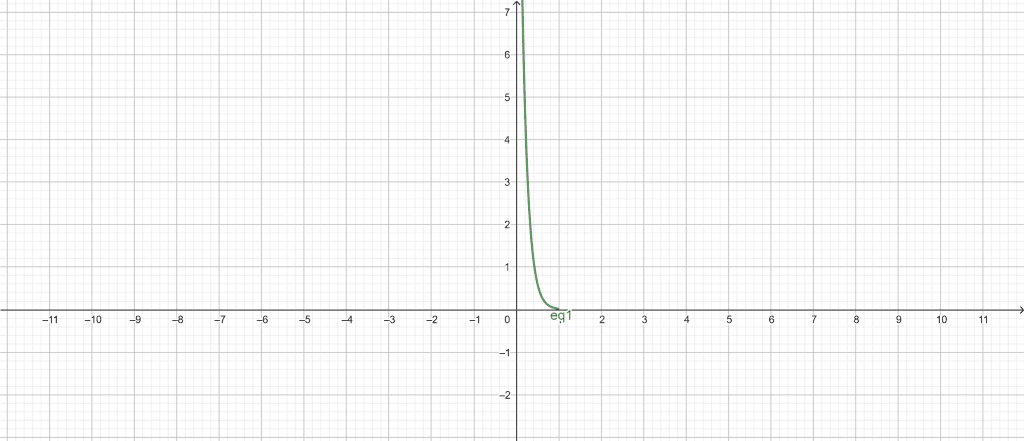
Figure 1
Example 2
A chemist has a beaker containing some formic acid with a molarity of 0.00008 \ M. The chemist needs to find the pH value of this weak Acid to perform a chemical reaction. Using the molarity of the Acid, calculate the pH value.
Solution
We can use the Acid-Base Calculator to calculate the pH value of the Acid instantly. Initially, we plug our molar value into the Acid-Base Calculator, which is 0.00008 \ M. After adding the molar value, we enter the name of the weak Acid in its respective box, formic Acid.
Finally, after plugging all inputs, we click the “Submit” button on our Acid-Base Calculator. The Acid-Base Calculator opens a new window and displays the pH values along with some additional information.
The results from the Acid-Base Calculator are shown below:
Input Interpretation:
0.00008 M formic acid
Result:
4.22
Acid-Base information:
Ka = 0.000177
pKa = 3.75
pH = 4.22
\[ [H_{3}O^{+}] = 5.98\times 10^{-5} \ \frac{mol}{L} \ (moles \ per \ liter) \]
pOH = 9.78
\[ OH^{-} = 1.67\times 10^{-10} \ \frac{mol}{L} \ (moles \ per \ liter) \]
% ionization = 74.8%
pH vs concentration plot:
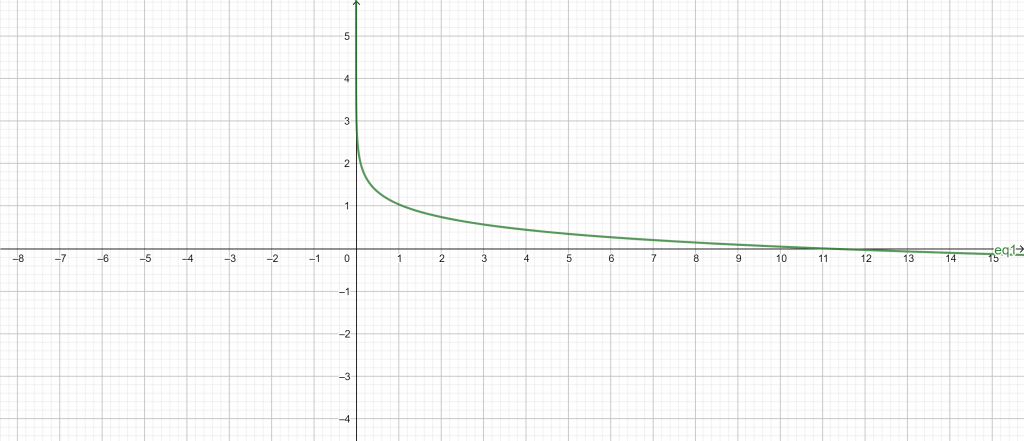
Figure 2
All images/graphs are created using GeoGebra.
