JUMP TO TOPIC
Area of Region Calculator + Online Solver With Free Steps
The online Area of Region Calculator is a calculator that helps you find the area between two intersecting lines.
The Area of Region Calculator is a powerful tool that mathematicians and scientists can use to calculate the areas of variable regions. The Area of Region Calculator is used in several fields like engineering, mathematics, and statistics.

What Is an Area of Region Calculator?
The Area of Region Calculator is an online tool that helps you calculate the area between the intersection of two curves or lines.
The Area of Region Calculator requires four inputs: the first line function, the second line function, the left bound of the function, and the right bound.
After inputting the values in the Area of Region Calculator, the calculator displays the area between the region and a plotted graph showing both the curves intersecting.
How To Use an Area of Region Calculator?
To use the Area of Region Calculator, you first plug in all the necessary inputs and click the “Submit” button.
The step-by-step instructions on how to use the Area of Region Calculator are given below:
Step 1
First, you plug your first line function into the Area of Region Calculator.
Step 2
After entering the first line function, you enter your second line function into your Area of Region Calculator.
Step 3
Once you enter your second line function, you the left bound value.
Step 4
In the last box, you enter the right bound value.
Step 5
Finally, after entering all the values into the Area of Region Calculator, you click the “Submit” button. The calculator will compute the results and display them in a new window. The results would comprise the area of the intersecting area and a plotted graph.
How Does an Area of Region Calculator Work?
The Area of Region Calculator works by taking in the curve function as input and integrating it to find the areas between the curves. The general formula for the area of a region is as follows:
\[ Area = \int_{a}^{b}[f(x)-g(x)] dx \]
The calculator then uses these functions to plot a graph.
How To Calculate Area Between Two Curves?
You can calculate the area between two curves, the region where two crossing curves lie, using integral calculus. Where the equation for two curves and their intersection locations are known, integration can be used to get the area beneath the curves.
To discover the approximate area of two curves, we must first split the area into numerous little rectangular strips parallel to the y-axis, starting at x = a and ending at x = b. Then, using integration, we can combine the areas of these small strips to obtain the approximate area of the two curves.
These rectangular strips will be dx in width and f(x)-g in height (x). By utilising integration inside the boundaries of x = a and x = b, we can now find the area between these two lines or curves. The area of the small rectangular strip is given by the expression dx(f(x) – g(x)).
Assuming that f(x) and g(x) are continuous on [a, b] and that g(x), f(x) for all x in [a, b], the following formula can be used:
\[ Area = \int_{a}^{b}[f(x)-g(x)] dx \]
Solved Examples
The Area of Region Calculator provides you with instantaneous results. Here are some examples solved using the Area of Region Calculator:
Example 1
A high school student is provided the following two equations:
\[ f(x)=9-(\frac{x}{2})^{2} \]
g(x) = 6-x
With a range of [-2,6]. Using the equations above, calculate the area between the two curves.
Solution
We can use the Area of Region Calculator to solve this equation. First, we enter the first line equation,$f(x)=9-(\frac{x}{2})^{2}$. We then plug the second line equation, g(x) = 6-x. After inputting both the equations we enter the range, [-2,6].
Once we are done entering the equations, we click the “Submit” button. The calculator finds the area between the regions and plots a graph in a new window.
The following results are from the Area of Region Calculator:
Input Interpretation:
Area between:
\[ f(x)=9-(\frac{x}{2})^{2} \ and \ g(x) = 6-x \]
Domain:
\[ -2 \leq x \leq 6 \]
Results:
\[ \int_{-2}^{6}\left ( 3 + x \frac{x^{2}}{4} \right )dx = \frac{64}{3} \approx 21.3333 \]
Plot:
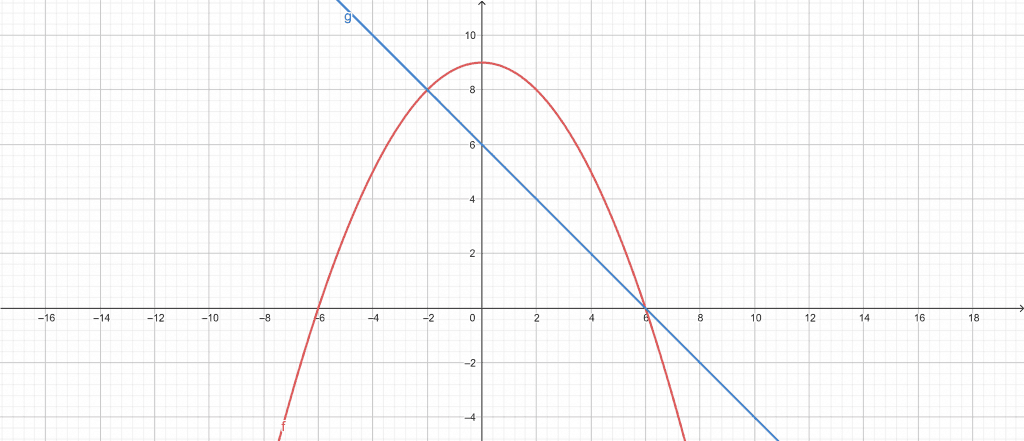
Figure 1
Example 2
A mathematician needs to calculate the area between two intersecting curves. He is given the following equations along with the domain:
\[ f(x)= 2x^{2}+5x \]
\[ g(x)=8x^{2} \]
\[ 0 \leq x \leq 0.83 \]
Using the Area of Region Calculator, find the area between these two curves.
Solution
The Area of Region Calculator can help us find the area between the two curves quickly. Initially, we enter our first function equation,$f(x)= 2x^{2}+5x$, into our Area of Region Calculator. After adding the first equation, we move on and enter our second curve equation,$g(x)=8x^{2}$, in the calculator. After plugging in the line equations, we add the domain of the equations,$0 \leq x \leq 0.83$.
Once we are done entering the inputs, we click on the “Submit” button on our Area of Region Calculator. The calculator quickly computes the results in a new window. The results show the area between the two curves and a plot graph.
The following results are extracted using the Area of Region Calculator:
Input Interpretation:
Area between:
\[ f(x)= 2x^{2}+5x \ and \ g(x)=8x^{2} \]
Domain:
\[ 0 \leq x \leq 0.83 \]
Results:
\[ \int_{0}^{0.83} = \left ( 5x – 6x^{2} \right )dx = 0.578676 \]
Plot:
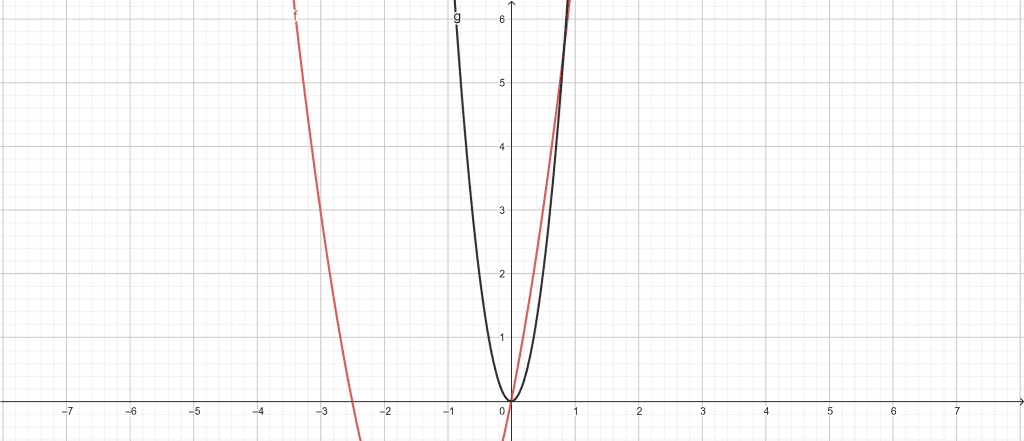
Figure 2
Example 3
Consider the following equations:
\[ f(x) = 2x^{2} \]
g(x) = x + 2
\[ -0.7 \leq x \leq 1.25 \]
Find the area between these two lines.
Solution
Using the Area of Region Calculator, we can find the area between the intersected lines. First, plug the equations into our calculator and add the domain range. Now click the “Submit” button on the Area of Region Calculator.
The following results are from the Area of Region Calculator:
Input Interpretation:
Area between:
\[ f(x) = 2x^{2} \ and \ g(x) = x + 2 \]
Domain:
\[ -0.7 \leq x \leq 1.25 \]
Results:
\[ \int_{-0.7}^{1.25} = \left ( 2 + x – 2x^{2} \right )dx = 2.9055 \]
Plot:
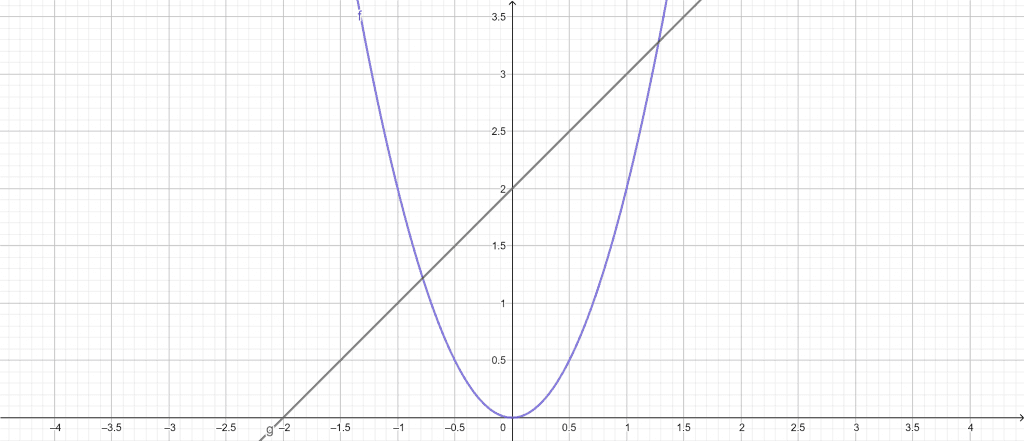
Figure 3
All images/graphs are made using GeoGebra.
