JUMP TO TOPIC
Boolean Algebra Calculator + Online Solver With Free Steps
A Boolean Algebra Calculator is used to calculate Boolean logic and solve simple as well as complex Boolean Algebraic problems.
This calculator can solve the different properties of Boolean Algebra, catering for commutative, associative, etc, which makes it best for solving complex Boolean Algebraic expressions.
The Boolean Logic here corresponds to the binary logical values which are used to represent mathematical results where the inputs vary from one binary state to another to generate an output response in the system.

What Is a Boolean Algebra Calculator?
A Boolean Algebra Calculator is a calculator which you can use to solve your Boolean Algebraic expressions online.
This calculator works in your browser via the internet and solves the given problem for you. The calculator is designed to solve Boolean expressions denoted in the correct format.
The Boolean Algebra Calculator, therefore, receives an expression with logic gates correlating the quantities given. These logic gates here are similar to numerical operators in standard algebraic equations.
You can enter your problems in the input box available, where the logic gates have to be typed into the system like AND, OR, etc.
How To Use the Boolean Algebra Calculator
To use the Boolean Algebra Calculator properly, a set of instructions must be followed. First, you must have a Boolean Algebraic expression to solve. In this expression, the gates are to be expressed as AND, OR, etc., therefore, no symbols are to be used.
The use of parenthesis in the proper fashion is very important. The lack of parenthesis can get the calculator confused and cause problems.
Now, you can follow the given steps to get the best results from your Boolean Algebra Calculator:
Step 1:
You are to start by entering the Boolean algebraic expression into the input box labeled, “Enter the statement:”.
Step 2:
You may also want to make sure that the given instructions are followed, and that the correct names and parenthesis for expressions are used.
Step 3:
Then, you can simply click the “Submit” button, and your results will appear in a new window. This new window is interactable and you can view all the different types of representations for your answer.
Step 4:
Finally, you can keep solving more problems by simply changing the input values in the input box in the new window.
It may be noted that this calculator can work for very complex problems relating to logic gates, but it does not provide support for inequalities and limits. In terms of complex Boolean expressions, if the input is put in properly, it will solve your problem and provide the results required.
How Does a Boolean Algebra Calculator Work?
A Boolean Algebra Calculator works by first breaking down a Boolean Algebraic expression into its constituent logical functions, and then calculating each instance according to the rules of precedence.
The rules of precedence in Boolean algebra tend to work very much like the ones in mathematical algebra. A numerical operator applied on a set of parentheses is applied to everything present within the parenthesis. The same is the case with Boolean algebra where a logical gate is applied to every entry present within the parenthesis.
This is how a Boolean algebraic equation is simplified and then solved.
Boolean Algebra
The branch of algebra that deals with mathematical logic and its operations are called Boolean Algebra. There are only two quantities in this whole branch of algebra, and these two are True and False. The True and False quantities are also commonly denoted by 1 and 0.
These values are thus expressed in terms of variables that would carry said values.
As in standard algebra, numerical operators are used to correlate numbers, in Boolean Algebra gates are used to correlate states. The gates are certain logical operations that result in their corresponding outputs. These outputs are represented as Truth Tables. The values in a truth table are designed to cater to every possible logical combination.
So for two variables this combination is $2^2$, which equates to 4, thus there are 4 possible logical outcomes from two variables. A generalized result of this combination number would be $2^n$, equating to n number of logical outcomes.
Logic Gates
Logic Gates are logical operations that can be performed on one or more binary inputs to get the desired result. They are usually thought of as a device output or a phenomenon of nature that corresponds with their output. Logic gates are therefore used to describe logical operations and their outputs for any number of logical input combinations.
There are a total of 8 most common logic gates used to build almost any logical operation and any logic gate imaginable. These are AND, OR, NOT, XOR, XNOR, NAND, NOR, and buffer. The three building blocks are Negation, Disjunction, and Conjunction, referring to NOT, OR, and AND, respectively.
Truth Tables
A Truth Table is used to express a logical relationship between one or more binary inputs in a tabular form. Truth Tables can bring a lot of insight into a problem that you may have to build a logic gate for. We know that any kind of logic gate can be made from the three building block gates being AND, OR, and NOT. That is done by using the output of an unknown logic gate in the form of a truth table.
Now, if you have the outputs corresponding to the inputs of a system that you would like to design logically, you can easily build a logical solution to whatever problem you are working with using those three gates.
The basic truth tables for AND, OR, and NOT gate are as follows:
AND Gate:
\[\begin{array}{C|C|C} A & B & Out \\ T & T & T \\ T & F & F \\ F & T & F \\ F & F & F \\ \end{array}\]
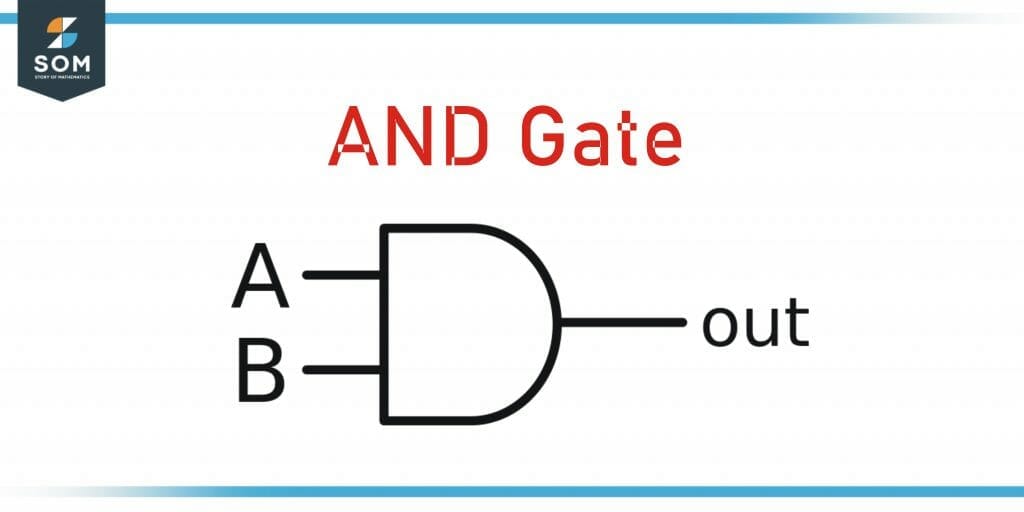
Figure 2 AND Gate
OR Gate:
\[\begin{array}{C|C|C} A & B & Out \\ T & T & T \\ T & F & T \\ F & T & T \\ F & F & F \\ \end{array}\]
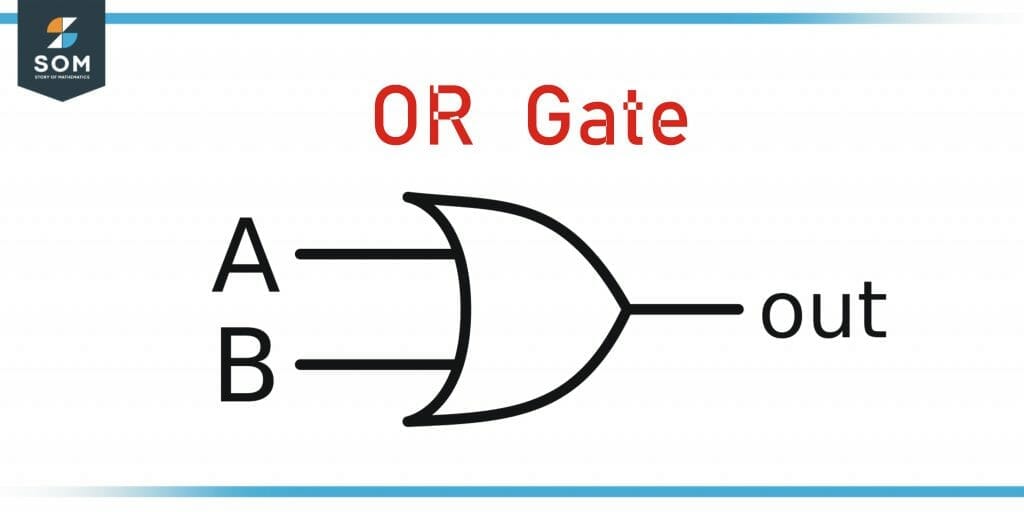
Figure 3 OR Gate
NOT Gate:
\[\begin{array}{C|C}A & Out \\ T & F \\ F & T\\ \end{array}\]
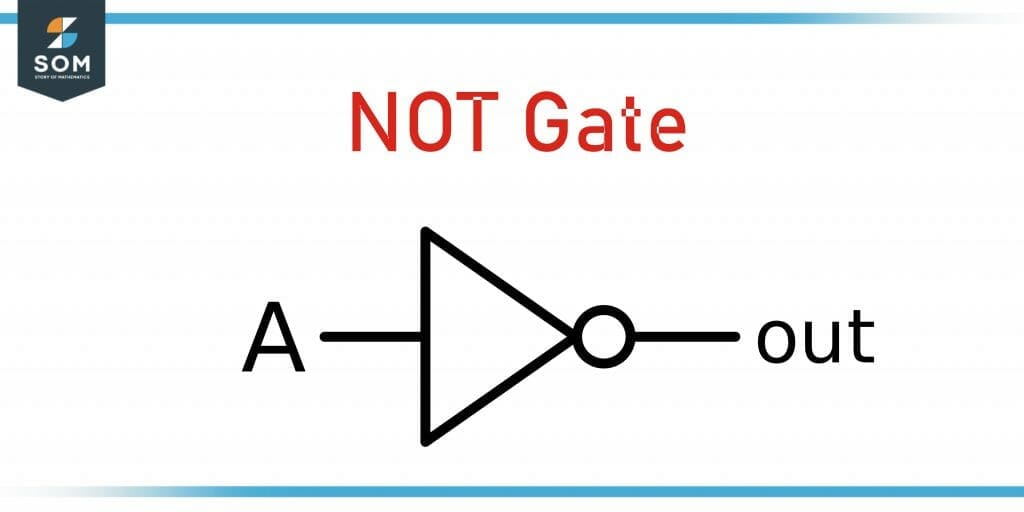
Figure 4 NOT Gate
Logic Expressions
The Logic Expressions are the opposite of a Truth Table as they use logic operators and variables to define a system. These are what you would want to find using a Truth Table, and these can easily be used to calculate the corresponding truth table of the system.
The Boolean Algebra Calculator is also designed to solve Logic Expression problems where the calculator finds the truth table to the problem by solving each node of the expression based on precedence.
History of Boolean Algebra
Boolean Algebra originated in England around the 1840s by the famous mathematician George Boole. The principles brought forward by him paved the way for many other mathematicians to come. Therefore, a whole branch of mathematics was named after him in 1913 by the American Logician Henry M. Sheffer.
Later research into the field of Boolean Algebra led to its linkage with the set theory and its significance in building mathematical logic. Over the years, this field has grown and evolved a lot. Now, it forms the basis for most engineering processes, specifically ones involved in electronics engineering.
Solved Examples
Example 1
Consider the following problem: NOT (p AND ((NOT p) OR q)) OR q. Solve this Boolean Algebraic expression to get the result.
We start by analyzing the given expression for the logical precedence provided. The precedence can be observed by looking at the parenthesis in the expression, so we begin to solve from the outside like we would any other algebraic expression. Applying NOT on the whole of pAND((NOTp)ORq) results in:
(NOTp)AND(NOT((NOTp)ORq)) = (NOTp)AND(pOR(NOTq))
Now we substitute our answer here into the expression and look for more simplification options.
((NOTp)AND(NOT((NOTp)ORq)))ORq = ((NOTp)AND(pOR(NOTq)))ORq
This is final simplified version of this expression, you can now solve it for its truth table.
\[\begin{array}{C|C|C|C|C|C|C} p & q & p^{not} & q^{not} & p\lor q^{not} & \smash{\overbrace{p^{not } \land (p\lor q^{not}) }^{\textbf{(a)}}} & a \lor q \\ T & T & F & F & T & F & T \\ T & F & F & T & T & F & F \\ F & T & T & F & F & F & T \\ F & F & T & T & T & T & T \\ \end{array}\]
Example 2
Consider the following problem: (NOTp)ORq. Solve this Boolean Algebraic expression to get the result.
We start by analyzing the given expression for the logical precedence provided. The precedence can be observed by looking at the parenthesis in the expression, so we begin to solve from the outside like we would any other algebraic expression.
But this expression is already simplified, so we start building its truth table.
\[\begin{array}{C|C|C|C|C} p & q & p^{not} & p^{not} \lor q \\ T & T & F & T \\ T & F & F & F \\ F & T & T & T \\ F & F & T & T \\ \end{array}\]
