JUMP TO TOPIC
Centripetal Force Calculator
The online Centripetal Force Calculator is a helpful tool for calculating the centripetal acceleration of an object. The force that tends to rotate an object in a circular path is known as centripetal force.
Whereas the acceleration of such objects is called centripetal acceleration. The calculator takes in the velocity and radius of the circle to calculate this acceleration.

Centripetal Force Calculator and Its Applications
A Centripetal Force Calculator is an online calculator that allows you to find the centripetal acceleration, provided that the velocity and circular radius is given.
The centripetal force has various applications in our daily life. For example, driving a car on curves, orbital systems, electrons revolving around the nucleus, and circular motions in machines like grinding or washing machines.
The acceleration of an object having circular motion can be easily obtained by a simple formula but you can calculate it quickly using the Centripetal Force Calculator.
It is an efficient tool that helps students and researchers of physics to solve problems related to centripetal force.
Procedure For Using Calculator
You can use the Centripetal Force Calculator by putting several values of the two quantities: velocity and radius of the circle. It requires only these quantities for performing the calculation.
There are some steps that you must follow to obtain the best results from this tool.
Step 1
Enter the velocity of the object in the ‘Velocity’ box. It takes the value of velocity in the ‘m/s’ unit. In case you have velocity in some other unit system, convert it first in the required unit.
Step 2
Now enter the radius of the circular path in which the object is rotating in the ‘Radius’ box. It accepts values only in the ‘meters’ unit only.
Step 3
To gather the results, press the ‘Submit’ button at this point.
Output
The output of the calculator is split into multiple sections. First, it displays the information of the input where the user can confirm the input values are correctly inserted.
It gives the general formula that is used for calculating centripetal acceleration. It is the square of velocity divided by the radius of the circle.
Then the ‘Result’ section provides the calculated centripetal acceleration in three different units which are meters per second square(m/s$^{2}$), feet per second square(ft/s$^{2}$) and centimeters per second square(cm/s$^{2}$).
Working of the Calculator
The centripetal force calculator works by finding the centripetal acceleration for the given tangential velocity and radius. The working of this calculator can be better understood by first knowing the basic concept in physics that is related to centripetal force and tangential velocity.
After knowing these concepts, understanding centripetal acceleration will not be a more tedious task.
Centripetal Force
Centripetal force is the force that acts on an object moving in a circular path. It is directed towards the axis of rotation and its unit is Newton. The literal meaning of centripetal force is “center seeking.”
The direction of this force is always perpendicular to the object’s displacement. The centripetal force is equal to the product of mass and the square of tangential velocity whole divided by the radius of the circular path. This formula is given by:
\[F = mv^2/r\]
Where ‘F’ is the centripetal force, ‘m’ is the mass of the moving object, ‘v’ is the tangential velocity and ‘r’ is the radius.
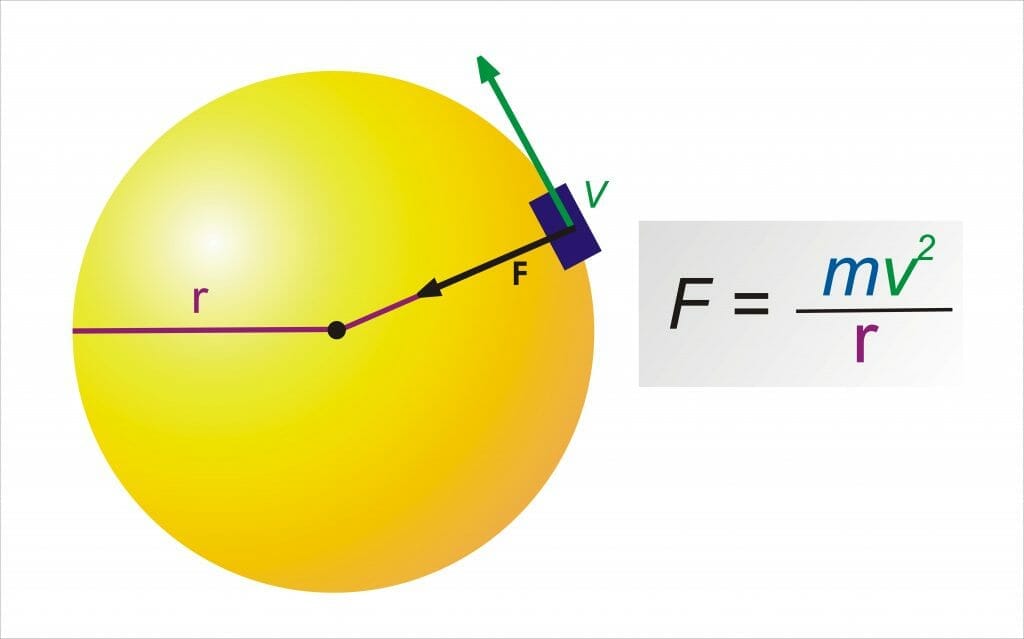
Figure 1
The above figure shows the direction of centripetal force and tangential velocity of the object moving in a circular path.
Tangential Velocity
Tangential velocity is the linear component of the object’s velocity when moving in a curvilinear path. This velocity describes the movement of a body across the edge of a circular path; its direction is always at the tangent to the circle.
A tangent is a line that touches only one point of a circle. The linear velocity is equal to the tangential velocity at any instance. The formula for tangential velocity is shown below:
v$_t$ = r * $\omega$
Where $\omega$ is the angular velocity and r is the radius of the circular path.
Centripetal Acceleration
Centripetal acceleration is the acceleration that brings about a movement of an object along a circular path. Its direction is radially towards the center of the circle resulting in perpendicular to the direction of tangential velocity.
Centripetal acceleration is also known as “radial” acceleration. Its unit is meters per second squared m/s$^2$. The acceleration is a change in velocity either in magnitude or direction or both.
The direction of velocity constantly changes in a uniform circular motion hence acceleration is always there. This acceleration encounters when turning a car in a curve. There is sideways acceleration because the direction of the car is changing.
The acceleration effect will become greater as the turning curve becomes sharper and the speed increases. This acceleration is known as centripetal acceleration and it is due to the centripetal force.
Its magnitude is equal to the square of the tangential velocity ‘v’ of the moving object divided by the distance ‘r’ from the center which is known as the radius of the circular path.
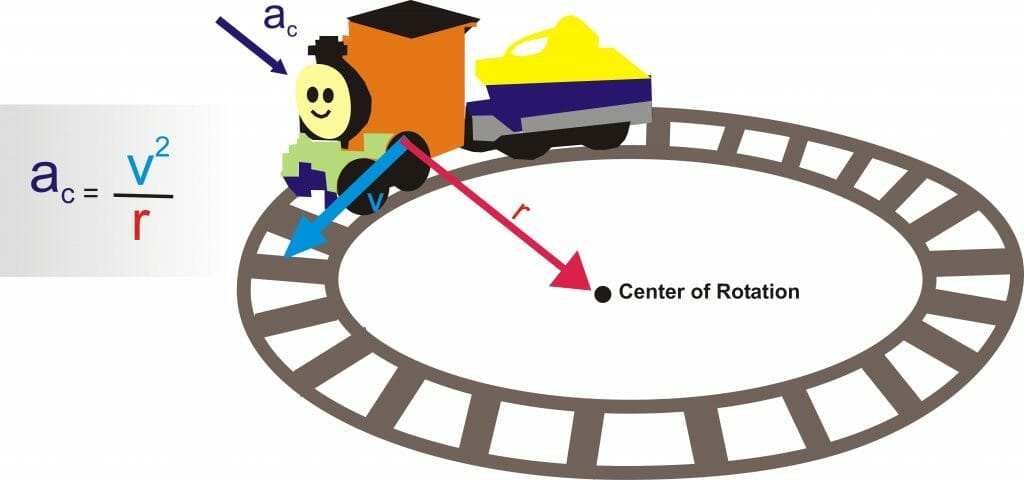
Figure 2
Mathematically the magnitude is given by the formula:
\[a_c = v^2/r\]
The above formula can also be written in terms of angular velocity by substituting v=r$\omega$ as:
a$_c$ = r x $\omega^2$
Solved Examples
Here are some examples for a better understanding of the calculator.
Example 1
A race car is running on a circular track having a radius of 50 meters. If the speed of the car is 28 m/s, what is the centripetal acceleration of the car?
Solution
The solution to this problem is given as follows:
Equation
The equation used to find the centripetal acceleration is:
a = v$^2$/r
Where ‘a’ represents the acceleration, ‘v’ represents the velocity and ‘c’ denotes the radius.
Result
The car is moving with the following acceleration.
Centripetal acceleration = 15.68 m/s$^{2}$ = 51.44 ft/s$^{2}$ = 1568 cm/s$^{2}$
Example 2
Consider an object moving with a velocity of 15 m/s in a 10-meter circular path. Find its centripetal acceleration.
Solution
Equation
a = v$^2$/r
Result
Centripetal acceleration = 22.5 m/s$^{2}$ = 73.82 ft/s$^{2}$ = 2250 cm/s$^{2}$
