Characteristic Polynomial Calculator + Online Solver With Free Steps

The online Characteristic Polynomial Calculator is a calculator that allows you to find the characteristic polynomial of a matrix.

The Characteristic Polynomial Calculator is a powerful tool that helps mathematicians and students quickly find the characteristic polynomial of a matrix without performing a lengthy calculation. 

What Is a Characteristic Polynomial Calculator?

A Characteristic Polynomial Calculator is an online tool that helps you quickly calculate the characteristic polynomial of a 3×3 matrix.

The Characteristic Polynomial Calculator requires three inputs: the matrix’s first, second, and third row. After inputting these values, the Characteristic Polynomial Calculator can easily find the characteristic polynomial.

How To Use a Characteristic Polynomial Calculator?

To use the Characteristic Polynomial Calculator, we plug in all the inputs necessary and click the “Submit” button.

The detailed instructions on how to use the Characteristic Polynomial Calculator can be found below:

Step 1

Initially, we enter the first row of the matrix into the Characteristic Polynomial Calculator. Make sure that you use the latex format while using this calculator.

Step 2

After entering the values of the first row, we enter the values of the second row of the matrix into the Characteristic Polynomial Calculator.

Step 3

Once you have entered the second-row values, you enter the values present in the third row into the Characteristic Polynomial Calculator.

Step 4

Finally, once all the values have been entered into the Characteristic Polynomial Calculator, you click the “Submit” button. The calculator will instantly show you the characteristics polynomial value of the 3×3 matrix. The calculator will plot a $y- \lambda$ graph in a new window.

How Does a Characteristic Polynomial Calculator Work?

A Characteristic Polynomial Calculator works by using the input values and calculating the characteristic polynomial of the 3×3 matrix. The calculator also uses the eigenvalues and the determinant of the matrix. The following formula is used to find the polynomial characteristic of a matrix:

\[ f(\lambda) = det(A – \lambda I_{n}) \]

What Is a Characteristic Polynomial?

A characteristic polynomial of a square matrix is a polynomial with the eigenvalues as roots and invariant under matrix similarity. By equating the characteristic polynomial to zero, the characteristic equation is created. The determinant equation is another name for it. The characteristic polynomial is also known as the Cayley Hamilton theorem.

Let’s say we are given a square matrix A with n rows and n columns. The characteristic polynomial of this matrix can be written as:

\[  f(\lambda) = det(A – \lambda I_{n}) \]

Here, $\lambda$ is a scalar quantity, det stands for the determinant operation, and $I _{n}$ is the identity matrix.

How to Find the Characteristic Polynomial of a 2×2 Matrix?

To find the characteristic polynomial of a 2×2 matrix, we can use $f(\lambda) = det(A – \lambda I_{n})$. We can find the characteristic polynomial by using the following method.

Considering matrix A now:

\[A = \begin{bmatrix}
5 & 2 \\
\ 2 & 1 \\
\end{bmatrix}\]

The matrix is a 2×2 matrix, so we can conclude that the identity matrix is: 

\[I = \begin{bmatrix}
1 & 0 \\
\ 0 & 1 \\
\end{bmatrix}\]

Now we can use these values and plug them in the characteristic polynomial formula $f(\lambda) = det(A – \lambda I_{n})$ which gives us the following result:

\[det \begin{bmatrix}
5-\lambda & 2 \\
\ 2 & 1-\lambda \\
\end{bmatrix}\]

By solving the above determinant, we get the following equation:

\[ \lambda^{2} – 6 \lambda + 1 \]

The above equation is the characteristic polynomial of the 2×2 matrix.

How to Find the Characteristic Polynomial of a 3×3 Matrix?

To calculate the characteristic polynomial of a 3×3 matrix, we use the following formula: 

\[ f(\lambda) = det(A – \lambda I_{3}) \]

Let us suppose a matrix A:

\[A = \begin{bmatrix}
-\lambda & 6 & 8 \\
\frac{1}{2} & -\lambda & 0\\
0 & \frac{1}{2} & 0
\end{bmatrix}\]

And I is the identity matrix which is:

\[ I = \begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0\\
0 & 0 & 1
\end{bmatrix}\]

Now plug in the values in the formula, and we get:

\[f(\lambda) = det\begin{bmatrix}
-\lambda & 6 & 8 \\
\frac{1}{2} & -\lambda & 0\\
0 & \frac{1}{2} & 0
\end{bmatrix}\]

After solving the equation, we get the characteristic polynomial of a 3×3 matrix as shown below:

\[ f(\lambda) = \lambda^{3} + 3\lambda + 2 \]

Solved Example

The Characteristic Polynomial Calculator is a fantastic tool that can help you calculate the characteristic polynomial of the 3×3 matrix instantly.

The following examples are solved using the Characteristic Polynomial Calculator:

Example 1

During an assignment, a college student comes across the following matrix:

\[A= \begin{bmatrix}
2 & 4 & 3 \\
3 & 1 & -4\\
7 & 18 & 3
\end{bmatrix}\]

To complete his assignment, the student must find the characteristic polynomial of the 3×3 matrix given. Using the Characteristic Polynomial Calculator, find the characteristic polynomial of the matrix.

Solution

Using the Characteristic Polynomial Calculator, we can easily find the characteristic polynomial of the matrix. First, we input the first row of the matrix into the Characteristic Polynomial Calculator; the first row of the matrix is [2 4 3]. After adding the first row into the calculator, enter the second row of the matrix into the Characteristic Polynomial Calculator; the values of the second row are [3 1 -4]. Now we enter the values located in the third row of the matrix into the calculator; the values of the third row are [7 18 3].

Finally, after entering all the values into the Characteristic Polynomial Calculator, we click the “Submit” button. The results are quickly shown below the calculator.

The following results are taken from the Characteristic Polynomial Calculator:

Input

\[\text{Characteristic Polynomial} = \begin{bmatrix}
2 & 4 & 3 \\
3 & 1 & -4\\
7 & 18 & 3
\end{bmatrix} \ (Variable)\]

Results

\[ -\lambda^{3}+6\lambda^{2}-50\lambda+143 \]

Plots

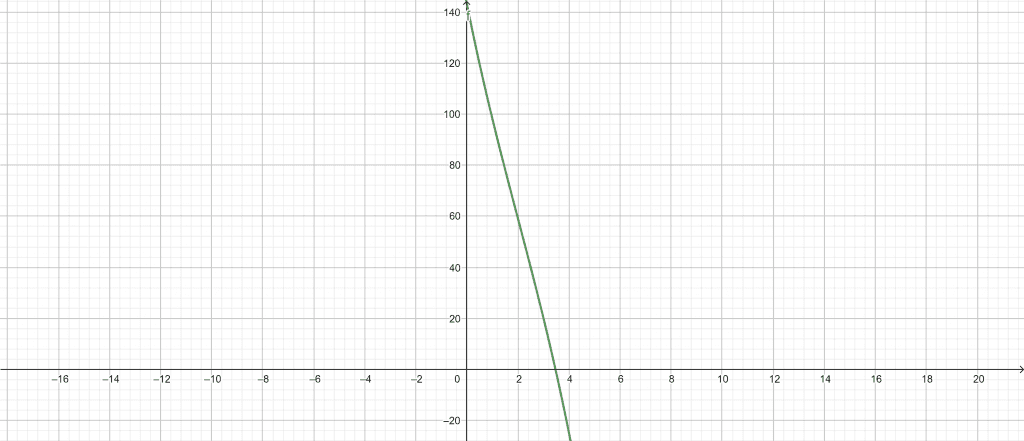
Figure 1

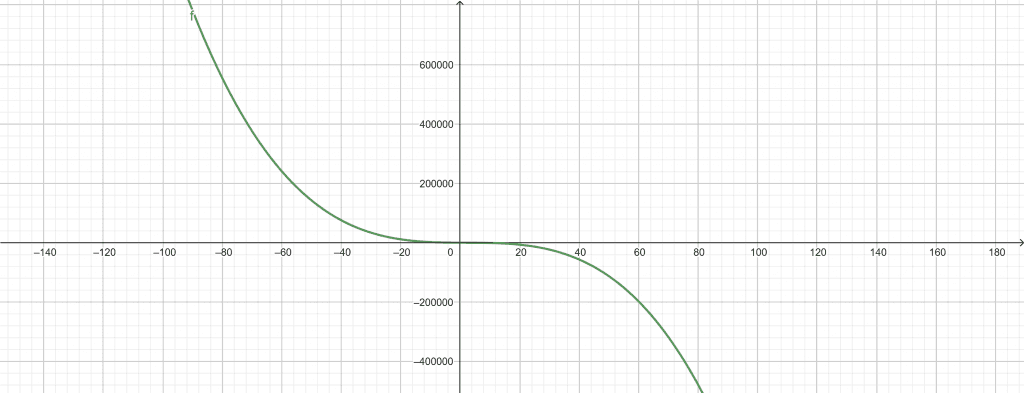
Figure 2

Alternate Forms

\[ 143-\lambda((\lambda-6)\lambda+50) \]

\[ \lambda((\lambda-6)\lambda-50)+143 \]

\[ -(\lambda-2)^{3}-38(\lambda – 2)+59 \]

Example 2

During his research, a mathematician comes across the following 3×3 matrix:

\[A= \begin{bmatrix}
3 & 5 & 6 \\
3 & 2 & 3\\
5 & 3 & -4
\end{bmatrix}\]

To complete his research, the mathematician needs to find the characteristics polynomial of the matrix given above. Use the Characteristic Polynomial Calculator to find the characteristic polynomial of the 3×3 matrix given.

Solution

We may simply find the matrix’s characteristic polynomial using the Characteristic Polynomial Calculator. First, we enter the first row of the matrix into the Characteristic Polynomial Calculator; the first row of the matrix is [3 5 6]. After entering the first row of the matrix into the calculator, enter the second row of the matrix into the Characteristic Polynomial Calculator; the values of the second row are [3 2 3]. Now we enter the numbers from the third row of the matrix into the calculator; the values from the third row are [5 3 -4].

Finally, we click the “Submit” button after inputting all data into the Characteristic Polynomial Calculator. The findings are displayed instantaneously below the calculator.

The Characteristic Polynomial Calculator yielded the following results:

Input

\[\text{Characteristic Polynomial}= \begin{bmatrix}
3 & 5 & 6 \\
3 & 2 & 3\\
5 & 3 & -4
\end{bmatrix} \ (Variable) \]

Result

\[ -\lambda^{3}+\lambda^{2}+68\lambda+78 \]

Plots

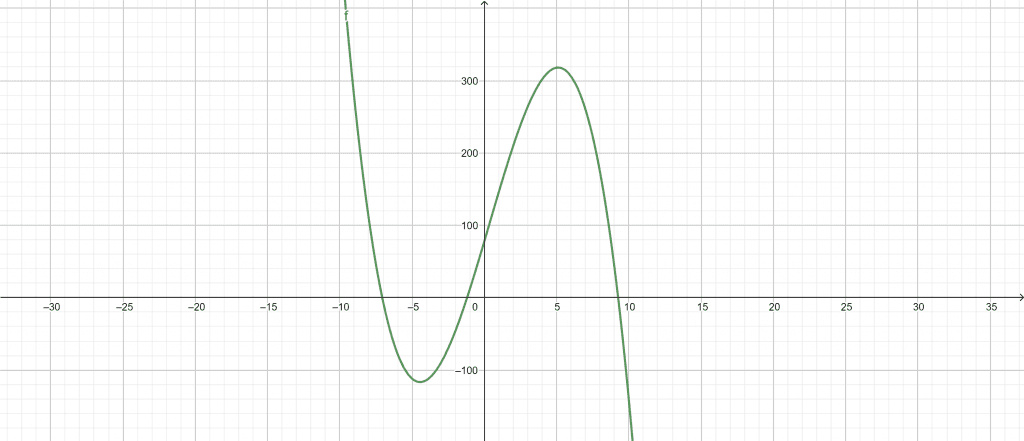
Figure 3

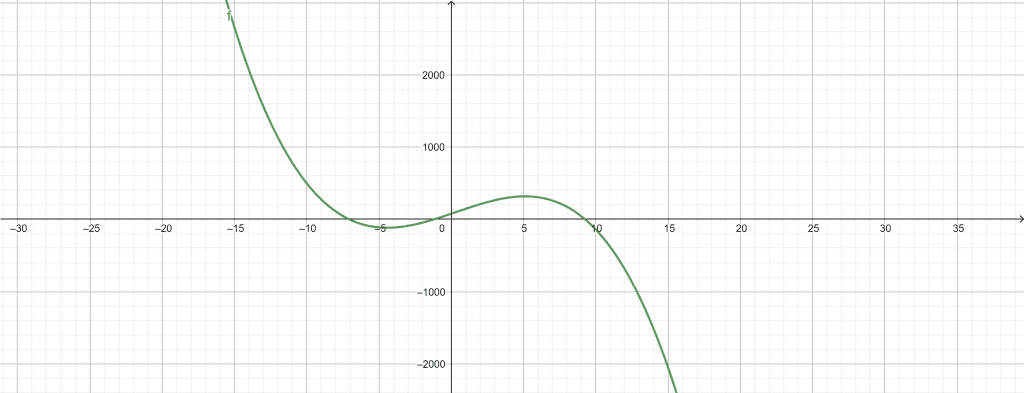
Figure 4

All images/graphs are made using GeoGebra.

Sleep Cycle Calculator < Math Calculators List > Proportion Calculator