JUMP TO TOPIC
Circle Area Calculator + Online Solver With Free Steps
The Circle Area Calculator finds a circle’s area given the circle’s radius using the “pi r squared” formula with pi rounded to two decimal places.
Note that the calculator expects a real, constant value as input. Therefore, avoid using variable names (such as x, y, z) and iota = $\sqrt{-1}$ since this makes your number complex. For such inputs, the calculator will display an error message.

What Is the Circle Area Calculator?
The Circle Area Calculator is an online tool that approximates the area of a circle given the circle’s radius using a = pi * r squared. The value of pi is rounded to two decimal places so pi = $\boldsymbol{\pi}$ = 3.14.
The calculator interface consists of a single text box labeled “A = 3.14 * <radius>” where the “<radius>” represents the value of the circle’s radius r. The radius must be a constant value since the calculator does not support variable inputs.
How To Use the Circle Area Calculator?
You can use the Circle Area Calculator to find the area of any circle by providing the value of that circle’s radius value. If you have the diameter instead of the radius, divide it by two first since r = d / 2.
Suppose that you want to find the area of a circle with diameter $\sqrt{2}$. Then, you can use the calculator for this purpose by following the step-by-step guidelines below.
Step 1
Ensure the radius value does not involve any variables (letters representing variables such as x, y, z, etc.). Our example does not have any variables – we can proceed safely.
Step 2
Enter the value of the radius into the text box. If you have the diameter instead of radius, enter the diameter and add “/2” at the end.
For the example above, since we have the diameter, you would enter “sqrt(2) / 2” without quotes to get the corresponding radius.
Step 3
Press the Submit button to get the results.
Results
The results contain two sections: “Input” and “Result.” The former displays the equation as finally interpreted by the calculator in mathematical form, while the latter shows the resulting area of the circle.
In our mock example, the results are:
A = 3.14 x 2$^\boldsymbol{\mathsf{2}}$
Result = 12.56
How Does the Circle Area Calculator Work?
The Circle Area Calculator works by applying the following formula with the given radius value:
\[ A_\text{circle} = \pi \times r^2 \]
Definition of Circles
In Euclidean geometry, a circle is a perfectly round, two-dimensional shape such that all points along it are equidistant from a certain point called the center. Mathematically, it is a set of points satisfying the equation x$^\mathsf{2}$ + y$^\mathsf{2}$ = r, where r represents the circle radius.
The circle’s boundary length (or perimeter) is the circumference, where C = 2 * pi * r. This formula comes from the definition of the mathematical constant pi ($\pi$), which we will look at shortly.
The circle radius is the distance from the circle’s center to any point along the circle boundary. The circle diameter is double the radius (d = 2 * r or r = d / 2) and represents the length of the line joining two points on a circle that PASSES through the center.
The “passing through the center” condition distinguishes the diameter from a chord, which is a line joining any two points on the circle. Therefore, the diameter is a special chord! The following figure visualizes these basic terms:
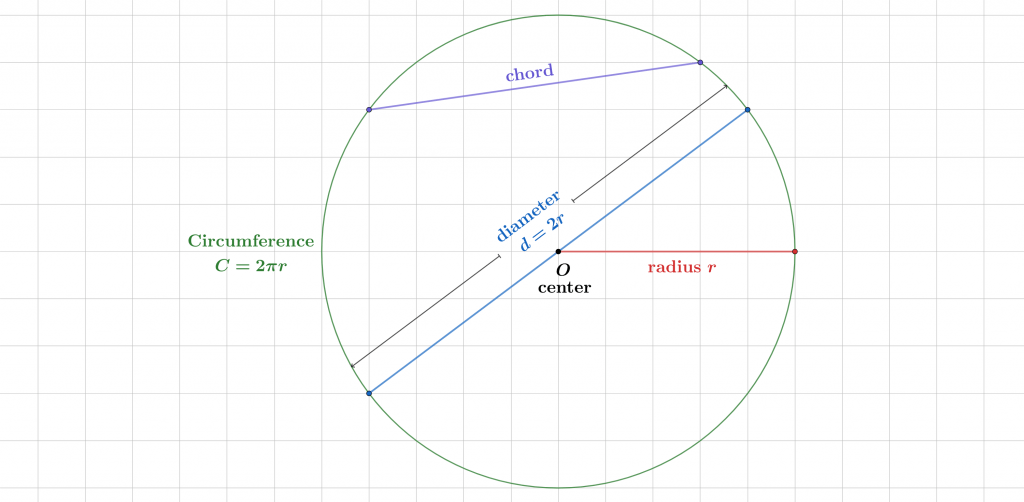
Figure 1
A part of a circle’s curve is called an arc.
Definition of Pi
$\pi$, pronounced “pie,” is a mathematical constant. It represents the ratio of a circle’s circumference to its diameter and is an irrational number (non-repeating and infinite).
\[ \pi = \frac{\text{circumference}}{\text{diameter}} = \frac{C}{D} = 3.1415926535… \]
Today, computers have estimated the value of $\pi$ up to trillions of digits. Even though one cannot write irrational numbers as fractions of the form p/q, $\pi$ is sometimes approximated by the fraction 22 / 7. For many commonly encountered calculations, this approximation is sufficient.
Area of Circle – Archimedes’ Proof
There are lots of proofs for the area of a circle. Some involve calculus while some involve a visual rearrangement. However, the simplest is Archimedes’ proof.
Basic Intuition
Consider a circular shape such as a pizza. Now imagine cutting it into four equal slices. Each slice approximately represents a triangle. A triangle has three straight sides, but one of the sides (the crust of the pizza forming the arc) of each slice is curved in this case.
So, the total area of the circle is greater than the sum of the area of each triangle. If the base of the triangle is $b$ and the height is $h$, then:
\[ A_\text{circle} \approx A_\text{triangles} = \sum_{i\,=\,1}^4 \frac{1}{2} \times b_i \times h_i \]
Here, note that if the triangles are inscribed within the circle:
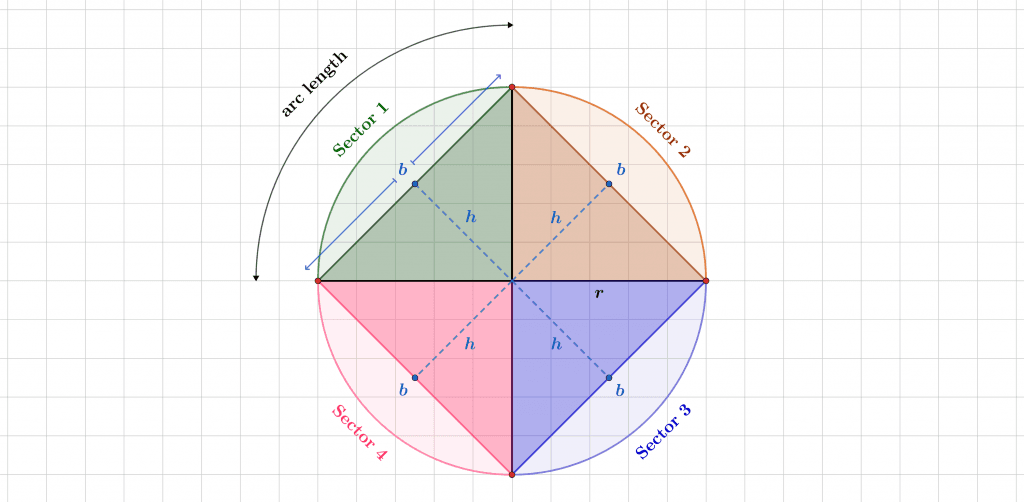
Figure 2
Then the following applies:
base < arc length, height < radius
$\boldsymbol{\therefore}$ area of circle > sum of the areas of the triangles
On the other hand, if the triangles are escribed as below:
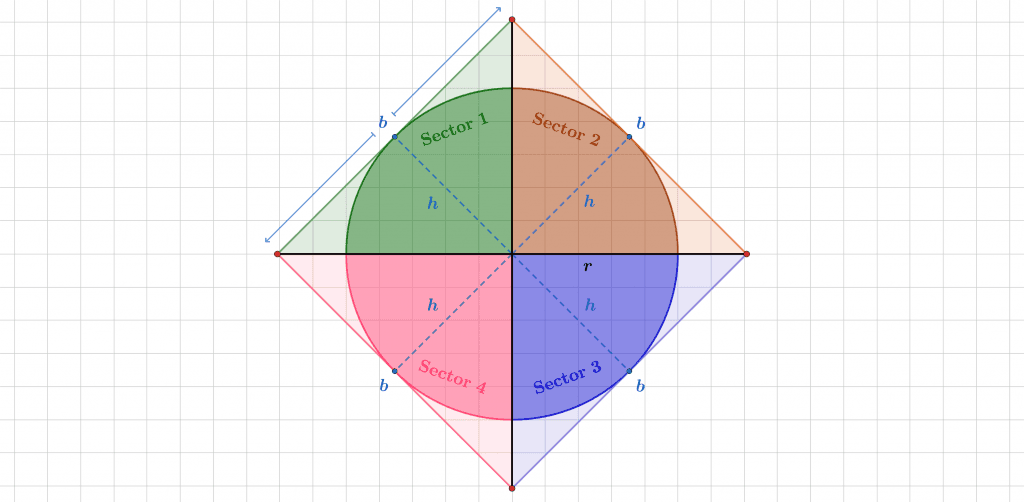
Figure 3
Then the following is true:
base > arc length, height = radius
$\boldsymbol{\therefore}$ area of circle < sum of the areas of the triangles
Extending to Limits
If you cut the same circle into infinitely many pieces, the curved part of each slice/sector becomes an infinitesimally small, straight line. Therefore, our triangular approximation becomes more accurate, and we can say that $A_\text{triangles} \to A_\text{circle}$, as the number of triangles n $\to \infty$.
In summary, a circle can be thought of as the limit of a sequence of regular polygons (e.g., triangles, squares, hexagons, etc.), and the area of the circle is then equal to the sum of each polygon! Now, an n-vertex polygon (with n > 3) can be represented by n triangles (n = 4 in Figures 2 and 3) such that:
\[ A_\text{polygon} = \frac{1}{2}\times q \times h \]
Where h is the height of each triangle making up the polygon and q is the perimeter of the polygon, which is equal to the combined sum of the base b of each triangle forming the polygon. That is:
\[ q = \sum_{i\,=\,1}^n b_i \]
If all the triangles occupy the same area (have equal base lengths), then q = n * b.
Final Formulation
Archimedes uses the above concepts to combine all these triangles into one, and states that a circle with circumference C and radius r has the same area as a single right-angled triangle with base b = C and height h = r:
\[ A_\text{circle} = A_\text{triangle} = \frac{1}{2} \times b \times h = \frac{1}{2} \times C \times r \]
\[ \Rightarrow \, A_\text{circle} = \frac{1}{2} \times 2 \pi r \times r = \pi r^2\]
Proof by Contradiction
Let us consider that the area of our circle is greater than the area of the triangle = $\boldsymbol{\frac{1}{2}rc=\pi r^2}$.
Then, we could inscribe an n-polygon inside it, and we can represent this with n triangles. The area of this polygon increases as we increase n, and will be very close to the circle’s area as n $\to \infty$.
However, using the concept of limits, we know that the height h of each triangle in the polygon will always be less than the actual radius of the circle, so h < r.
Furthermore, the base of each triangle will be smaller than the arc, meaning that the perimeter of the polygon will be smaller than the circumference, so q < C. You can see this in Figure 2.
Therefore:
\[ A_\text{polygon} \approx A_\text{circle} = \frac{1}{2}qh < \frac{1}{2}Cr = \pi r^2 = A_\text{triangle} \]
The above result contradicts our assumption!
Now, if we consider the area of the circle to be smaller than the area of the triangle, then we could draw an n-polygon around it (escribing, see Figure 3). As we increase the number of vertices n, the area of this polygon will shrink and will be very close to the area of the circle as n $\to \infty$.
In this case, using limits, we can see that the perimeter of the polygon will always be greater than the circumference, so q > C. However, the height h of each triangle forming the polygon always equals the radius, so h = r. You can visualize this in Figure 3. Therefore:
\[ A_\text{polygon} \approx A_\text{circle} = \frac{1}{2}qh > \frac{1}{2}Cr = \pi r^2 = A_\text{triangle} \]
Again, this result contradicts our assumption!
In conclusion, if the area of the circle is neither greater nor smaller than the area of this triangle, then the only possibility is that they are equal. Therefore:
\[ A_\text{circle} = A_\text{triangle} = \pi r^2 \]
Solved Examples
Example 1
Given a circle with a circumference of 3 cm, find its area.
Solution
Let pi = 3.14. Since circumference C = 2 * pi * r then:
radius r = C / (2 * pi) = 3 / (2 * 3.14) = 3 / 6.28
r = 0.47771 cm
As the area of a circle A = pi * r$^\mathsf{2}$:
A = 3.14 * 0.4771$^\mathsf{2}$
A = 0.71474 cm$^\boldsymbol{\mathsf{2}}$
All graphs/images were created with GeoGebra.
