JUMP TO TOPIC
Compound Inequality Calculator + Online Solver With Free Steps
The Compound Inequality Calculator is an online tool that helps to find the variable’s intervals on which the compound inequality exists. A compound inequality is simply the combination of two inequalities joined by a word.
The compound inequalities are of two types depending upon the joining word used to connect them. The compound inequality involving the word “and” is called a conjunction. While the disjunction compound inequality uses “or” as the connecting word.
The calculator finds the set of all possible values that satisfy the compound inequality and also graphically represents this set in the form of the number line.

What Is a Compound Inequality Calculator?
A Compound Inequality Calculator is an online tool that is designed to solve your compound inequality problems.
The compound inequalities represent a range of allowed values for a problem instead of only one value. They can be used for problems that demand the answer in a certain range like finding speed limits, the spread of a region, the capacity of a container, etc.
Therefore, compound inequalities are frequently observed in the areas of physics and engineering. To solve these inequalities manually, you must know and practice various techniques to obtain the solutions.
Besides having a good grip on mathematics, you need to spend a portion of your precious time solving these inequalities. In the era of modern technology, there is no need to solve such problems by hand when online tools like this calculator are just a click away from you.
You can use the Compound Inequality Calculator to save your time and resources. It is one of the best online tools that deal with compound inequality-related problems quickly and gives the most accurate results.
You can find this handy calculator anytime in your browser without any downloading and installation. The calculator’s interface is very friendly and easy to use as it simply needs the inequalities of your problem. Rest it assures you to get the exact solution to the problem.
How To Use the Compound Inequality Calculator?
To use the Compound Inequality Calculator, you must have two inequalities with the same unknown variable and know the type of your compound inequality. Once you have these elements you can enter them in input fields and just by pressing a button it will solve the whole problem for you.
To get the best results from Compound Inequality Calculator, you need to follow every step mentioned in the instructions below.
Step 1
You can start by simply inserting the first inequality of the compound inequality. Enter the one side of the inequality in the left box, select the respective sign and then enter the other side of the inequality.
Step 2
Now you need to specify the type of compound inequality by choosing one of the two available options. The two options are “and” and “or.” Always select it according to your problem.
Step 3
After this, enter the second inequality of the compound inequality. Insert both sides and the appropriate sign for the inequality.
Step 4
The total compound inequality is entered until now. At the last press of the Solve button, you will acquire the solution.
Result
The solution is displayed in the three sections. The first section displays the interpretation of the calculator for your problem. It is a safety check where you can ensure that your problem is correctly interpreted.
The second section gives the interval of the unknown variable for which the compound inequality exists. Finally, the third section graphically presents the interval specified in the second section.
The graph is always in the form of a number line as we have only one variable in such problems. This line is the common region of both the sub-intervals obtained after solving inequalities.
A filled dot indicates that the point lies inside the interval while an empty dot denotes that the point lies outside of the interval.
How Does the Compound Inequality Calculator Work?
The Compound Inequality calculator works by accepting the inequalities and solving them for an unknown variable, and the Compound Inequality is obtained by joining two inequalities. Before we move toward this topic we should know what inequality is in algebra.
What Is an Inequality?
Inequalities are mathematical expressions that are not equal on both sides. It is the relationship of expression which have a nonequal comparison. The equal sign in between the equation is replaced by greater than, greater than or equal to, less than, less than, or equal to sign.
There are different types of inequalities such as Polynomial inequalities, Absolute value inequalities, and rational inequalities.
Polynomial Inequalities
Polynomial inequalities contain polynomial on both sides of the inequality. Polynomial inequalities are further divided into different types but the most important ones are Linear inequalities and Quadratic inequalities.
Linear Inequalities
Linear inequalities involve polynomial of degree 1. The expression on both sides of inequality must be a polynomial having the highest power equal to one.
These inequalities can be solved by simplifying the inequalities expressions for the required variables.
Quadratic Inequalities
Quadratic inequalities can be obtained from quadratic equations. The word “quadratic” is derived from the word “quadrature” which means “square” hence these inequalities contain the polynomial having the highest power equal to two.
The quadratic expression is either greater than or less than some number in these inequalities. The standard form of quadratic inequality is given as:
\[ ax^2 + bx + c > 0 \]
Or
\[ ax^2 + bx + c < 0 \]
Absolute Value Inequalities
These inequalities have the expressions inside the absolute value sign. The absolute value of the variable is represented by the mod or modulus sign. This value of the number represents its magnitude or the distance from the origin.
Since the distance is always positive, the absolute value of a number is always a non-negative number. The minus sign is used along with the numeric value to represent the direction sometimes.
However, to obtain absolute value, the numeric value is considered only and the minus sign is ignored. The expression of this inequality is given by:
|ax +b| > c
Rational Inequalities
Rational inequalities consist of rational expressions. Rational expressions are those expressions that can be written in $\frac{p}{q}$ form. While solving these inequalities, we should take care of those values for which these expressions are undefined.
Therefore we excluded those values for which expression gives infinite numbers.
Compound Inequalities
A compound inequality is an amalgam of two inequalities joined together by “and” or “or.” This calculator solves this inequality when we insert any compound inequalities.
The inequalities which are combined are those which we discussed above such as it can be linear, quadratic, absolute value, and rational. The method to solve each inequality is the same as solving normal inequality.
But the combined solution of both inequalities depends on whether they are joined by “and” or “or.” There are two types of compound inequalities depending on the word which joined them.
The two types of compound inequalities are Conjunction and Disjunction, which are explained in detail below.
Conjunction
It is the inequality in which both the inequalities are combined by “AND.” It requires both of the inequalities to be true for the given values of the solution and if one of them is false both are false.
The combined solution set of this inequality is an intersection of the solution set of individual inequalities and can be represented by using the $\cap$ symbol.
In conjunction, it is not necessary to write “and” between two inequalities always, for instance, 5<x<10 is conjunction but there is no “and” written between them since it is understood.
Disjunction
The inequalities are joined together by “OR” in Disjunction. In this, the given values of the solution can be true for either or both of the inequalities.
The union of solution sets of individual inequalities results in a solution set of disjunction. This solution set can be denoted by using the $\cup$ symbol. This inequality is always shown using the “or” word.
Compound Inequality Graph
The compound inequalities can be represented graphically on a number line and depending on the type of inequality, the resultant solution can be drawn on the number line.
Graphing Compound Inequality With AND
The inequalities with “and” can be represented on a number line by first graphing the individual inequalities above the number line. If the inequality is either $\le$ or $\ge$, then draw a closed dot at the endpoint of the graph otherwise draw the open dot.
Then for the final graph, find the intersection of two individual graphs and draw it on the number line as represented by the following figure 1.
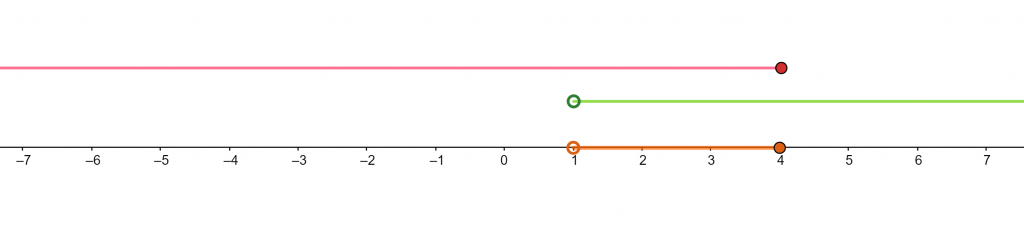
Figure 1
Graphing Compound Inequality With OR
This inequality can be shown on a graph by first drawing both of the inequalities above the number line. If the inequality is with $\le$ or $\ge$, then make a closed dot at the endpoint of the graph otherwise make the open dot.
Then for the resultant graph of disjunction, take the union of both of the graphs and represent it on the number line as shown below in figure 2.

Figure 2
How To Solve Compound Inequalities
The compound inequality is made up of two inequalities connected by the word “and” or “or.” This can be solved in the same manner as normal inequalities solved, and then we joined both the solution sets depending on the word which combined both of the inequalities.
Solving these inequalities means finding all the values for which it stands true. If the inequalities are joined by the word “and” then the solution consists of all the values for which both of the inequalities are true.
If these inequalities are connected by the word “or” then all the values for which either or both the inequalities are true is a required solution.
To solve compound inequalities, separate both inequalities and solve them just as simple inequality, and when the inequality is multiplied or divided by a negative number reverse its sign.
After this, graph the solution of each inequality on the number line. To find the resultant graph, take the union of individual graphs if there is “or” or intersection if there is “and.”
Solved Examples
Let’s have a look at some examples solved by the Compound Inequality Calculator. The examples are explained one by one in the section below.
Example 1
Consider the following conjunction compound inequality:
3x + 2 < 14
and
2x – 5 > -11
Find the interval of x for which this inequality exists.
Solution
Solving it with the calculator gives the following output:
-3 < x < 4
Number Line
Figure 3 depicts the interval for x in form of the number line. The line represents the intersection of the two inequalities as the input inequality is of conjunction type. The points x = -3 and x = 4 are not included in interval so they are represented with empty dots.
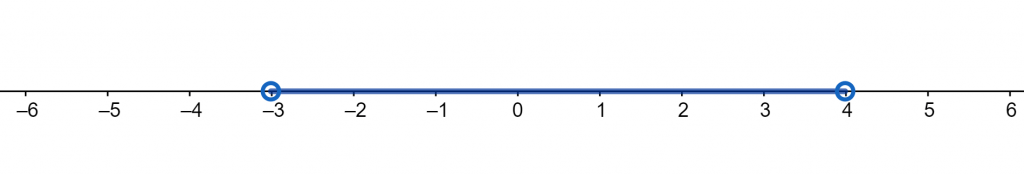
Figure 3
Example 2
Consider the following disjunction compound inequality:
5z +7 < 27
or
\[-3z \le 18 \]
Solve for z using Compound Inequality Calculator.
Solution
The interval of the variable z for the given inequality is given as:
\[ -6 \ge z < 4 \]
Number Line
The range of z is presented as a number line in figure 4. As the point, x = -6 is included in the interval so it is represented by a filled dot whereas the other point x = 4 is not inside the interval so it is denoted by an empty dot.
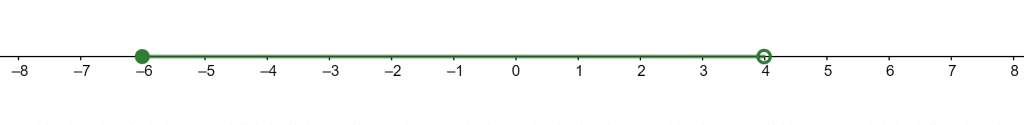
Figure 4
The solution to the disjunction inequality is normally represented separately for sub-interval from each inequality. Like in this example two different graphs for $z \ge -6$ and z < 4 can be drawn but the calculator gives a common interval that is $ -6 \ge z < 4 $.
Example 3
Solve the following conjunction compound inequality and draw the solution on the number line.
\[ 2x -3 \ge -2 \]
and
2x – 3 < 5
Solution
When you insert the above inequality in the calculator it gives the following output.
\[ \frac{1}{2} \le x < 4 \]
Number Line
The number line for input inequality is illustrated in figure 5.
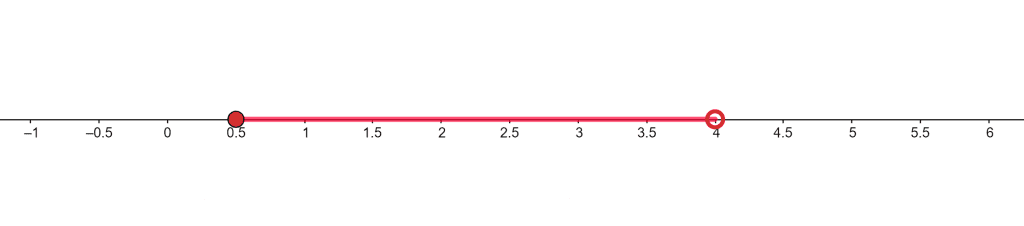
Figure 5
In the above number line, the circle at 0.5 is filled because 0.5 is included in the solution whereas the circle at 4 is empty. After all, it is not included in the solution.
All the Mathematical Images/Graphs are created using GeoGebra.
