JUMP TO TOPIC
Difference Quotient Calculator + Online Solver with Free Steps
A Difference Quotient Calculator is an online tool that is used to calculate the difference quotients for any function f(x). This calculator is used to obtain accurate and quick results for the difference quotient for any function f(x).
The Difference Quotient Calculator is very simple to use as it takes the input from the user and provides the answer in a matter of seconds. The Difference Quotient Calculator can work for all types of functions, be it polynomial or trigonometric functions.
The Difference Quotient Calculator is a free tool that provides the answers in detail. It provides the output in both simplified and non-simplified forms, so the user can choose any which one they prefer.

What Is a Difference Quotient Calculator?
A Difference Quotient Calculator is the best online tool available on the internet to calculate the difference quotients for all types of functions f(x).
It provides the output answer in two forms; one being a simplified form and the other one being the non-simplified form.
The Difference Quotient Calculator is an excellent tool that provides simplified answers for all types of functions in a matter of seconds. All the user has to do is input the function f(x) and the function f(x+h) and obtain the desired results by clicking on the “Submit” button.
The Difference Quotient Calculator makes use of the following formula for calculating the difference quotients for functions:
\[ \text{Difference Quotient} = \frac {f(x+h) – f(x)} {h} \]
The Difference Quotient Calculator takes two inputs from the user — one being the function f(x) and the other being the function incorporating the distance factor, which is h, hence the input function f(x+h).
Once these values of the functions are inserted, all the user has to do is click on the button that says “Submit.” The Difference Quotient Calculator then instantly simulates the solution and presents the output.
The output from the Difference Quotient Calculator is displayed in three sections — one displaying the input in the formula, the other showing the non-simplified solution, and finally, the last section displays the solution in the most simplified form.
How To Use the Difference Quotient Calculator?
You can use the Difference Quotient Calculator by entering the functions in specified blocks on the calculator. The Difference Quotient Calculator is fairly simple to use due to its user-friendly interface.
The interface of the Difference Quotient Calculator consists of two input boxes. The first input box is titled as f(x) and it prompts the user to insert the function f(x). The second input box is titled as f(x+h) and it prompts the user to insert the function f(x+h), which is the function incorporating the distance factor h.
Apart from the two input boxes, the Difference Quotient Calculator displays the output in three separate sections.
A step-by-step guide for using the Difference Quotient Calculator is given below:
Step 1
First, analyze the function and identify which type of function it is. The Difference Quotient Calculator can calculate difference quotients for all kinds of functions.
Step 2
Once you have analyzed your function, the next step is to insert the inputs into the Difference Quotient Calculator. There are two input boxes: one titled f(x) and the other one titled as f(x+h). Insert the values functions into their respective input boxes.
Step 3
After inserting the inputs, click on the button that says “Submit.” Identifying this button is not difficult at all due to the simple interface of the Difference Quotient Calculator.
Step 4
Upon clicking on the “Submit” button, the Difference Quotient Calculator will begin the simulation. The best feature of this calculator is that it only takes a few seconds to load the solution.
Step 5
The solution obtained from the Difference Quotient Calculator is displayed in three different sections. These three different sections are given below:
Input Section
The first section is the Input Section. This section displays the input functions incorporated into the following formula:
\[ \text{Difference Quotient} = \frac {f(x+h) – f(x)} {h} \]
Result Section
This section displays the result of the difference quotient for the function f(x). The result viewed in this section is in a non-simplified form since it is obtained by simply inserting the values of the functions in the following formula:
\[ \text{Difference Quotient} = \frac {f(x+h) – f(x)} {h} \]
Alternate Form Section
The final section is the Alternate Form section. This section displays the answer to the difference quotient in the most simplified form. The display of the solution in three different sections enables the user to interpret the solution of the difference quotient in great detail.
How Does the Difference Quotient Calculator Work?
The Difference Quotient Calculator works by using the difference quotient technique. It is the most efficient calculator in the realm of calculus. This calculator accurately displays one of the most profound concepts of calculus, which is the difference quotient.
To understand the working of the calculator, let’s review the concept of Difference Quotients.
What Is the Difference Quotient?
The Difference Quotient is the average rate of change of a function in a specified interval. The concept of difference quotient extends out in the definition of derivative of any function f(x). The difference quotient, when extended, results in the derivative of the function.
As the name “Difference Quotient” suggests, its formula incorporates both factors — the difference as well as the quotient. This indicates that the difference quotient hints toward the concept of slopes and secant lines, which will be discussed later on.
The difference quotient for any function f(x) represents the difference of the function f(x) with the function f(x+h). The function f(x+h) is the same as the function f(x) but it varies with a slight distance which is h, which is the distance between x and x+h.
The difference quotient expresses this input difference to the quotient of the difference x and x+h. This relation is expressed in the following formula:
\[ \text{Difference Quotient} = \frac {f(x+h) – f(x)} {h} \]
Graphical Representation of the Difference Quotient
The best way to understand the concept of the difference quotient is to interpret it graphically. Since the words “difference” and “quotient” hint toward the slope formula, hence the difference quotient gives the slope of the secant line on the curve of the functions.
For comprehending the graphical interpretation, let’s revisit the definition of the secant line. The secant line is a line that passed through any two points on the curve.
To fully understand the graphical representation of the difference quotient, let’s think of it this way: there are two points around which the curve is plotted. The first point is (x, f(x)) and the next point is (x+h, f(x+h)).
The graphical representation of this concept of the difference quotient is shown below in Figure 1:
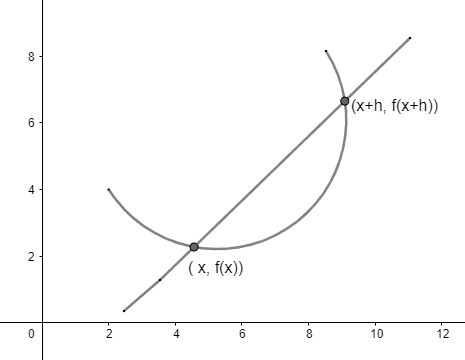
Figure 1
From the graph, the following formula can be interpreted on the basis of the standard slope formula:
\[ \text{Difference Quotient} = \frac {f(x+h) – f(x)} {x+h-x} \]
Simplifying this formula gives us:
\[ \text{Difference Quotient} = \frac {f(x+h) – f(x)} {h} \]
How To Derive the Derivative of the Function From Its Difference Quotient
The derivative of any function f(x) can be derived from the difference quotient by taking the limit of the difference quotient. This limit is obtained by taking the following assumption:
\[ h \rightarrow 0 \]
Hence, by taking this limit, the derivative of the function f(x) can be obtained as shown below:
\[ \lim_{h\rightarrow 0} \frac {f(x+h) – f(x)} {h} \]
Inserting the values into this formula gives the same result as the first derivative of the function f(x).
The derivative of any function f(x) is defined as the rate at which the given function is changing at any given point. The derivative of a function is also referred to as the instantaneous rate of change.
Solved Examples
Here are a few examples that will help you to understand the functionality of the Difference Quotient Calculator.
Example 1
Find the difference quotient for the following function:
f(x) = 3x -5
Solution
Before using the Difference Quotient Calculator, let’s first analyze the function. The function is quite simple and is given below:
f(x) = 3x – 5
This function will act as the first input for the calculator. For the second input, substitute x with x+h in the function f(x) to obtain f(x+h). The function f(x+h) turns out to be:
f(x+h) = 3(x+h) – 5
Now, insert these two functions f(x) and f(x+h) in their respective input boxes and then click on the button that says Submit.
The Difference Quotient Calculator will take a few seconds to load the solution and then will present the solution in three different sections – the input section, the result section, and the alternate form section.
Input Section:
The input section displays the following input:
\[ \text{Difference Quotient} = \frac {3(x+h) -5 -(3x-5)} {h} \]
Display Section:
The result section displays the following result:
Difference Quotient = 3
Since the answer is already simplified, hence the third section of the simplified form is not displayed.
Hence, the difference quotient of this function f(x) turns out to be:
Difference Quotient = 3
Example 2
For the following function f(x), find the difference quotient:
\[ f(x) = x^{2} + 7x \]
Solution
Let’s analyze the function first. The function is given below:
\[ f(x) = x^2+7x \]
Upon analyzing the function, it appears to be a polynomial function. Hence, this function appears to be our first input value for the calculator.
Now, for the second input value for the Difference Quotient Calculator, insert x+h instead of x in the function f(x). This gives us f(x+h). This function f(x+h) is given below:
\[ f(x+h) = (x+h)^{2} + 7(x+h) \]
Now that we have both the inputs for the calculator, we can simply insert them into the calculator and then press the Submit button.
Upon pressing the submit button, the output gets displayed in three different sections. These three sections are given below:
Input Section:
The following input gets displayed in the input section:
\[ \text{Difference Quotient} = \frac {(x+h)^{2} + 7(x+h) – (x^{2} + 7x) } {h} \]
Result Section:
The result section displays the non-simplified result which is given as stated below:
\[ \text{Difference Quotient} = \frac {(x+h)^{2} + 7(x+h) – x^{2} – 7x} {h} \]
Alternate Form Section:
This section displays the answer in the most simplified form and it is given as shown below:
Difference Quotient = h + 2x +7
Hence the difference quotient for the given function f(x) turns out to be:
Difference Quotient = h + 2x +7
Example 3
Calculate the difference quotient for the function shown below:
f(x) = x + lnx
Solution
The first step is to analyze the given function. Upon analyzing this function, it appears to be a logarithmic function. The function is given below:
f(x) = x+lnx
This function acts as our first input for the difference quotient calculator.
Now for the second input for the calculator, replace x with x+h in the given function. Upon replacing this factor, the following function is obtained:
f(x+h) = (x+h) + ln(x+h)
Now that we have the two input values for the calculator, simply click on Submit to obtain the output. The output appears in three different sections.
Input Section
The first output is displayed in the input section. The input that is displayed is shown below:
\[ \text{Difference Quotient} = \frac { (x+h) + log(x+h) – (x + logx)} {h} \]
Result Section
The non-simplified difference quotient for this function f(x) is displayed in the result section and it is shown below:
\[ \text{Difference Quotient} = \frac { log (h+x) + h -logx} {h} \]
Alternate Form Section
This section displays the answer in the most simplified form. The most simplified form of the difference quotient for this function is given below:
\[ \text{Difference Quotient} = \frac {h-logx} {h} + \frac {log(h+x)} {h} \]
