JUMP TO TOPIC
- What Is the Domain and Range Calculator?
- How To Use the Domain and Range Calculator?
- How Does the Domain and Range Calculator Work?
- What are Functions?
- The Domain of a Function
- Range of a Function
- How To Find Domain and Range of a Function?
- Domain and Range of Exponential Functions
- Domain and Range of Rational Functions
- Domain and Range of Absolute Value Functions
- Domain and Range of Square Root Functions
- Domain and Range of Trigonometric Functions
- Solved Examples
Domain and Range Calculator + Online Solver With Free Steps
The online Domain and Range Calculator helps you to find the domain and range of the univariate mathematical functions. The function is provided as input to the calculator.
Domain means the set of all possible values for input whereas Range is the set of resulting values of output.
The calculator outputs the set of domain and range, the number line representation for both, and displays the graph of the function in the x-y plane.

What Is the Domain and Range Calculator?
The Domain and Range Calculator is an online tool that calculates the domain and range of the input function without any hassle.
To determine the domain for the function we need to put different values of the variable and check for which values function is defined. Then we put domain values in the function to get the set of output values which is the range of the function.
The concept of domain and range of the function is widely used in real-life problems. For instance, the capacity of the fuel tanks in vehicles and the respective distance they can cover. Similarly determining the perimeter of the pitch in a cricket stadium.
Also to verify the result we need to plot the graph of function which is also a tedious task.
Thus, we have a unique tool with its root in Engineering and Calculus. It can find domains and ranges for any sort of function at a very fast speed inside your browser with no prior requirements.
How To Use the Domain and Range Calculator?
You can use the Domain and Range Calculator by putting different kinds of univariate functions in the calculator. You will need to follow the simple steps below to use the calculator correctly.
Step 1
Enter the function in the box with the name Enter the function. This is the function for which you want to find domain and range. It should have only one independent variable.
Step 2
Now simply click the Calculate Domain and Range button to acquire the calculator’s answer.
Result
The result consists of multiple sections. It starts by giving the interval for the domain and range of the input function.
Then it represents both in a form of the number line. The number line is the single plane for one variable and each value is at a uniform distance in this line.
At the last, it plots the graph for the function so that one can better understand the region of the domain and range by visualizing it in the x-y plane. It can find these for any function like trigonometric, exponential, algebraic, etc.
How Does the Domain and Range Calculator Work?
This calculator works by finding the domain and range of a given function and plotting it on the number line and cartesian coordinate system.
This calculator finds the domain and range of any function including exponential, trigonometric, and absolute valued functions.
The information about the domain and range of a function is essential to know where the function is defined but before this, we should know about the functions.
What are Functions?
The process which relates each element ’a’ of a non-empty set A to the single element ’b’ of another non-empty set B is called the function. These functions are the basic part of calculus in mathematics.
The functions are the special types of the relation. A relation is defined as a function if every element of set A has only one image in set B. It can be represented by mapping or transformations.
The Domain of a Function
The set of all input values over which the function has defined outputs is called the domain of a function. It can also be defined as the set of all possible values for independent variables.
If a function is given by f:X $\rightarrow$ Y, then the domain of f is X. The domain of a function is represented by dom(f) = {x $\in$ R}.
Range of a Function
The range of a function is defined as the set of its possible output values. Suppose that there is a function defined by f:X $\rightarrow$ Y with domain X, then the range of f is the set Y which contains all of the output values of f.
The range of a function is denoted by ran(f) = {f(x):x $\in$ domain(f)}.
How To Find Domain and Range of a Function?
The domain and range can be found by considering the rules which are physically possible in real-life examples or the laws which are permitted in mathematics.
Finding the Domain of a Function
When there is a requirement to find the domain, first determine the type of given function. The function can be quadratic, trigonometric, or rational, and then evaluate the terms within the function equation.
Afterward, write the domain with proper notation. The domain written in proper notation includes the use of both parentheses () and square brackets [].
The parentheses are used when the number in the domain is not included but when the number is included in the domain, square brackets are used. If there is a need to use the infinity symbol, always use the parentheses.
Finding the Range of a Function
While finding the range of a function, first find out the type of function since there are different methods to find the range depending on the type of function.
Afterward, substitute the different values of x into the function equation to determine whether it is positive or negative. Then find the maximum and minimum values of the function as the range is spread over all values from minimum to maximum.
Finally, write the range with proper notation like the notation written for the domain.
Domain and Range of Exponential Functions
The exponential function of the form $y= a^x$ where $a \ge 0$ is defined for all real numbers. The domain of these given functions is all real numbers.
The exponential function always outputs the positive value for any value of the input. Therefore the range of these functions is all the positive real numbers excluding zero.
The domain and range can be written in proper notation as Domain= R and Range= (0, $\infty$).
Domain and Range of Rational Functions
A rational function is a function of the form $\frac{p(x)}{q(x)}$ where $q(x) \neq 0$. The domain of these functions consists of all real numbers except those values for which the denominator q(x) goes to zero.
When the denominator goes to zero, these functions take the indeterminant form, therefore these values are not included in the domain. These values of input x can be found by equating the denominator to zero and solving for x.
The range of rational functions includes all of its possible output values. When there is a rational function $f(x)= \frac{p(x)}{q(x)}$, replace f(x) with y. Then solve the equation for x and set the denominator of resultant equation to $\neq 0$.
Solve the resultant equation for y. Therefore, except for these values of y all the real numbers are the range of rational functions.
Domain and Range of Absolute Value Functions
The absolute value function is given by y=|ax+b|. The input to these functions can be all real numbers, hence the domain is the set of all real numbers.
The absolute value function always produces positive numbers for any input value. Therefore, the range is the set of all non-negative real numbers.
The domain and range of these functions can be written in the form as Domain= R and Range= [0, $\infty$).
Domain and Range of Square Root Functions
The function represented by $y= \sqrt{ax+b}$ is called a square root function. The square root of a negative number is not defined, therefore those values of the input which result in a negative term inside the square root must not be included in the domain.
The square root functions are defined for $x \ge-b/a$ in general, therefore the domain includes all the real numbers which are greater than or equal to -b/a.
The range of these functions is the set of all non-negative real numbers because these functions always give positive values as output since the square root of any number is always positive.
Domain and Range of Trigonometric Functions
The domain and range of trigonometric functions are defined as the input and output values of trigonometric functions. The domain of these functions represents those values of angles in degrees or radians for which these functions are defined.
The range gives the output value of the trigonometric function corresponding to a particular angle in the domain.
Solved Examples
Now let’s solve some examples by using this excellent calculator. Each example is described in detail below.
Example 1
Determine the domain and range of the following function:
\[ f(x) = \sqrt{x+4} \]
Solution
The solution to this problem by the calculator is as follows:
Domain
The set of all possible input values are:
\[ { x \in \mathbb{R} : x \ge -4 } \]
Range
The set of possible outcomes are:
\[ { y \in \mathbb{R} : y \ge 0 } \]
Number Lines
The number line representation for the domain is given in figure 1. The point x=4 is included in the interval and the arrowhead at the other end indicates the interval is up to infinity.
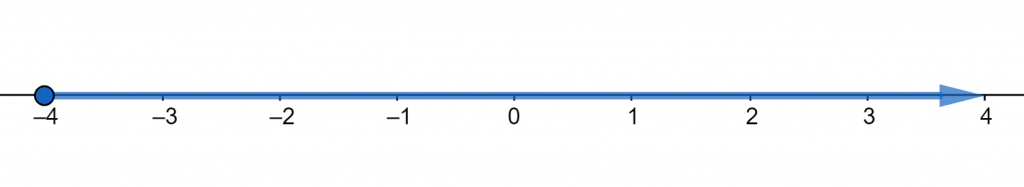
Figure 1
Similarly, the number line representation of the range is demonstrated in figure 2. It indicates the interval of y that is $[0, \inf)$
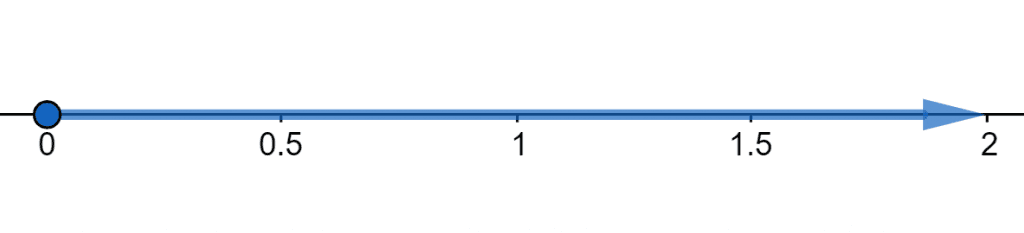
Figure 2
Plots
The plot for function $f(x)=\sqrt{x+4}$ for x=-8.2 to x=0.2 is given in figure 3.
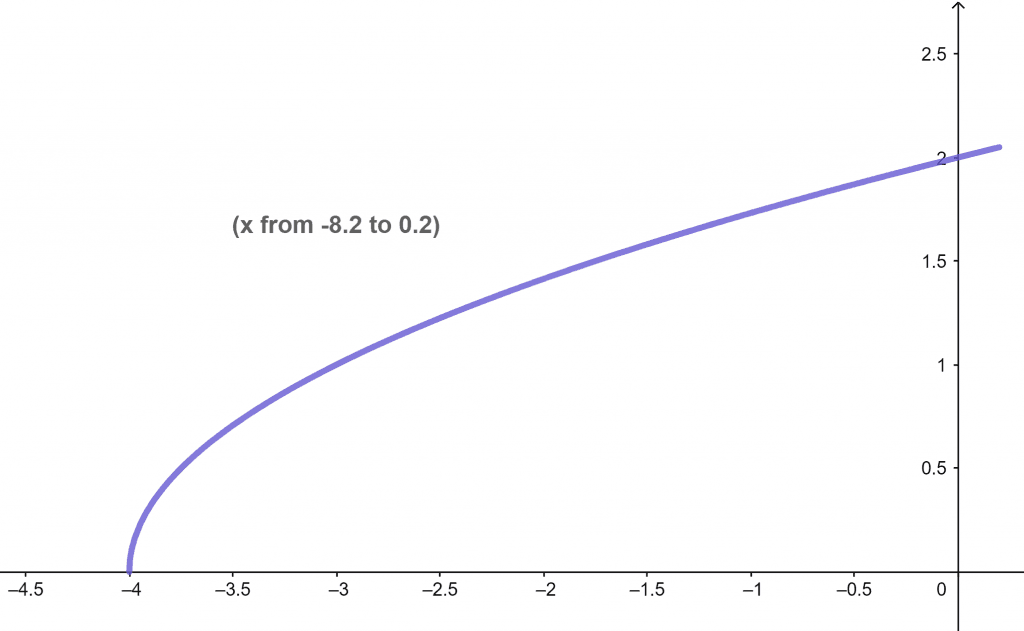
Figure 3
Figure 4 now represents the function from x=33.1 to x=25.1.
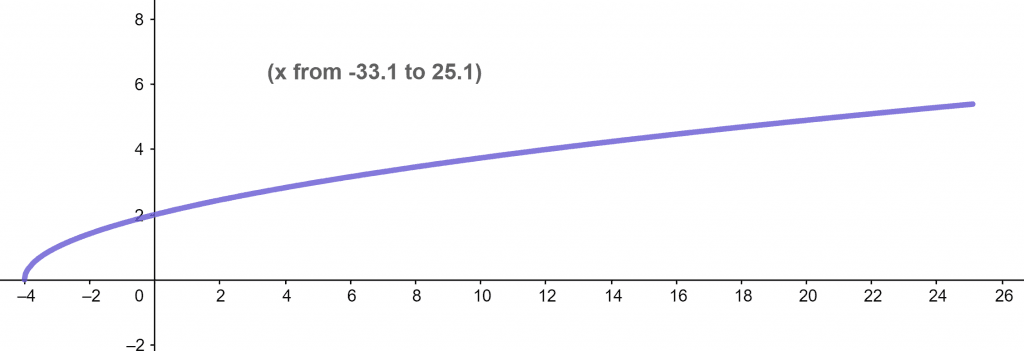
Figure 4
Example 2
Consider the below function:
f(x) = Cos(x)
Solution
Domain
The domain of function is given as:
\[ { \mathbb{R} \: (all \: real \: numbers) } \]
Range
The range of function is:
\[ { y \in \mathbb{R} : -1 \le y \le 1 } \]
Number lines
The number line representation for the domain is given in figure 5.
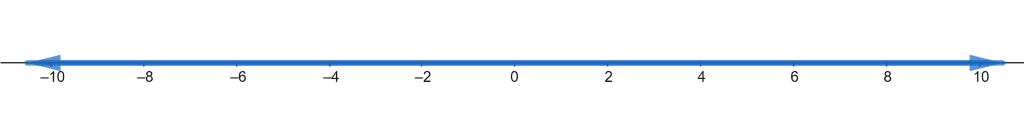
Figure 5
Similarly, the number line representation of the range is demonstrated in figure 6.
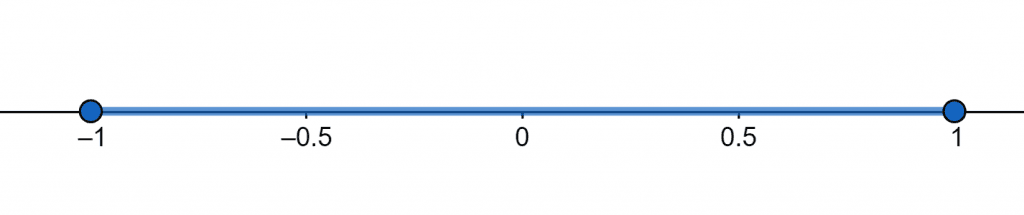
Figure 6
Plots
The plot for function f(x)=Cos(x) for smaller value of x is illustrated in following figure.
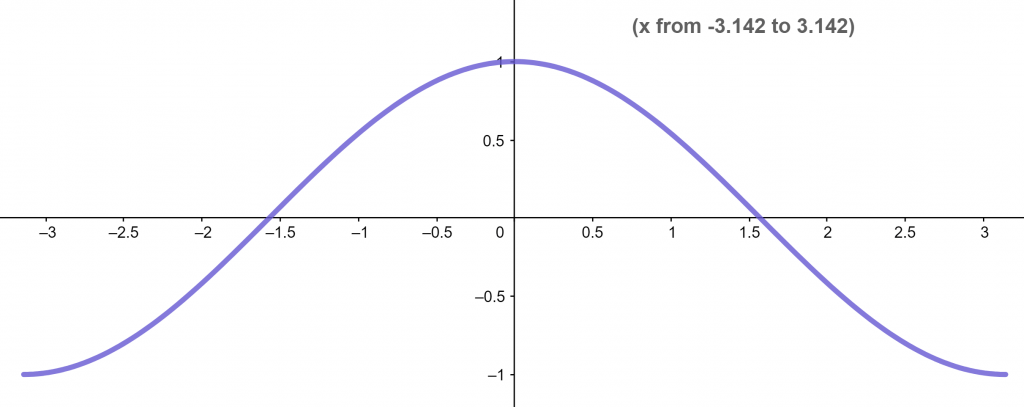
Figure 7
Now figure 8 is the graph for greater values of x.
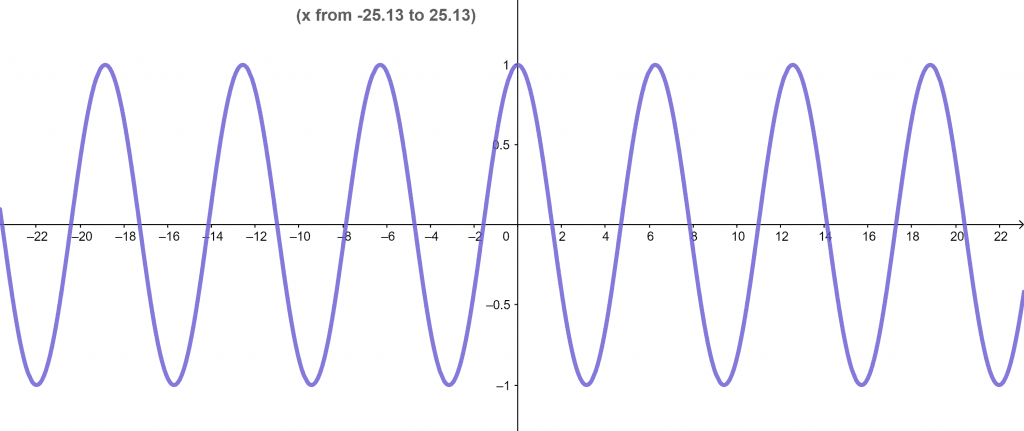
Figure 8
All the Mathematical Images/Graphs are created using GeoGebra.
