JUMP TO TOPIC
Inflection Points Calculator + Online Solver With Free Steps
The Inflection Points Calculator is a helpful tool that allows you to find the inflection point of a given function. This is the point where the concavity of a function changes its direction.
The Calculator requires the curve’s function as the input element and returns the inflection point and its graph.

What Is the Inflection Points Calculator?
The Inflection Points calculator is an online tool that can be used to find the point of inflection of a function using the function as an input. This calculator finds the point of the slope in which the rate of change of slope changes from increasing to decreasing manner or from decreasing to increasing manner. If you do this process by hand, it will take a lot of time and energy.
To quickly calculate the point of inflection without any effort, you can use the Inflection Points Calculator. The calculator works in all browsers without any need for prior downloading and installation.
This calculator performs the calculations in seconds and provides accurate values and graphs of the given function. If anyone has a good internet connection, he can use this calculator anywhere at any time.
Another feature of this calculator is that it is free and has no limit on the number of times you use it. Its usage is also very user friends, the details are mentioned in the next section.
How To Use the Inflection Points Calculator?
You can use the Inflection points calculator by adding the function of which the point of inflection you want to know in the given box. It is a calculator with a very simple window that has only one input box and a submit button for the processing of the results.
The procedure for using this calculator is very short and simple. You need to follow the steps mentioned below to properly use the calculator and get the results:
Step 1
Enter the function in the box labeled as ‘ Fit Equation’ for which you want to calculate the point of inflection. You should enter the complete equation with all the variables rightly placed and the exponents properly mentioned.
Step 2
Now click the “Submit” button to start the processing and get the results from the calculator.
Output
The output of the calculator consists of three sections. The first section shows the equation that has been entered and the calculator as worked on it. This section helps to verify the input function that you have entered.
Section two displays the mathematical results of the input functions. It displays a table in which the point of inflection, derivative, and type of curve is mentioned. This is the detailed output of the entered function.
Section three shows the plot of the function which indicates the point of inflection of the given function. This is a pictorial representation of the point of inflection.
How Does the Inflection Point Calculator Work?
The inflection points calculator works by finding the point of inflection for the given function and using the proper mathematical steps to find the inflection points of the curve.
The usage and functionality of this calculator will be cleared when you have an understanding of some basic concepts.
What Is an Inflection Point?
The inflection point or point of inflection is a point on a curve of a function at which the curvature changes its direction or sign. It is also known as flex or inflection. At this point, the concavity of the function changes.
What Is the Concavity Function?
The concavity of a function is the convex shape formed when the curve of a function bends. There are two types of concavities in a graph i.e. concave up and concave down.
How To Calculate the Inflection Point
The calculator determines the inflection point of the given point by following the steps mentioned below:
It takes the function from the user as input. Then it takes the first derivative of the entered function concerning the variable of the given function.
Then it performs the second derivative of the function and then it also solves the third derivative of the function. It confirms that the third derivative is not equal to zero.
Next, it makes the third derivative of the function equal to zero and finds the value of the variable. For knowing the maximum and minimum values it substitutes the value of the variable in the third derivative.
Now it replaces the value of the variable in the given function to find the value of the y coordinate, so the inflection point will be the obtained value from the function.
Solved Examples
For a better understanding of the Inflection Calculator, the following examples are solved step by step.
Example 1
Determine the point of inflection for the given function
f(x) = x^3 + 2
Solution
Given equation is:
y = f(x) = x^3 + 2
First, it calculates the first derivative:
f’(x) = 3x^2
Now, the second derivative:
f’’(x) = 6x
Lastly, the third derivative:
f’’’(x) = 6
It makes the second derivative equal to zero as:
6x = 0
x = 0
Now, it puts the value of x in the given function to find the value of y as:
y = 0^3 + 2
y = 2
Result
So the points of inflection are (0, 2).
Graph
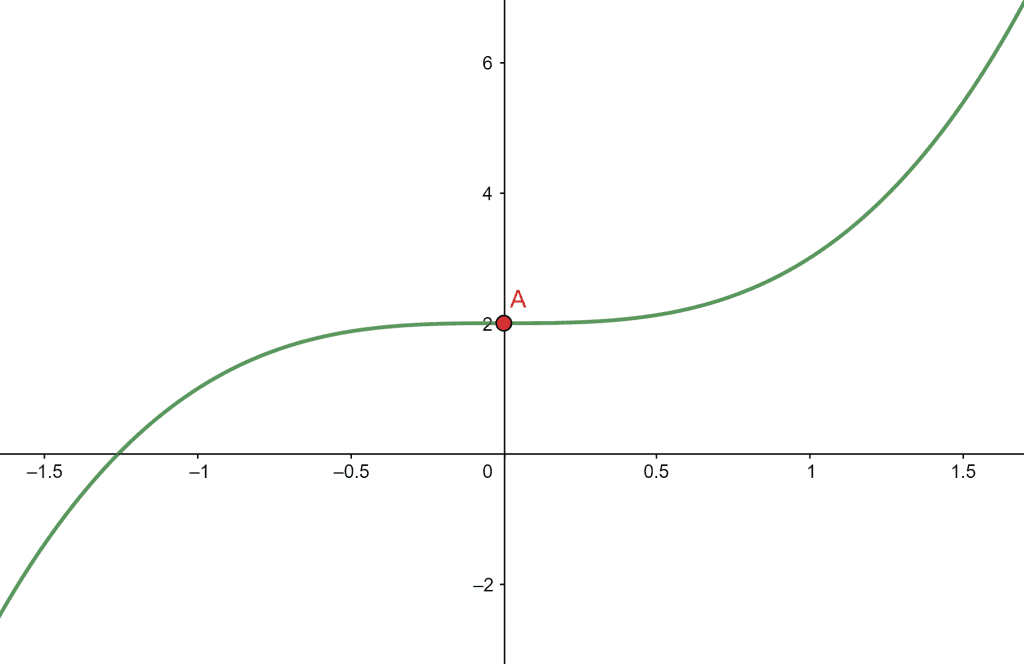
Figure 1
Example 2
Determine the point of inflection for the given function
f(x) = x^4 – 24x^2 + 11
Solution
Given equation is:
y = f(x) = x^4 – 24x^2 + 11
First, it calculates the first derivative:
f’(x) = 4x^3 – 48x
Now, the second derivative:
f’’(x) = 12x^2 – 48
Lastly, the third derivative:
f’’’(x) = 24x
It makes the second derivative equal to zero as:
12x^2 – 48 = 0
x = ± 2
Now, it puts the values of x in the given function one by one to find the value of y as:
For x = 2 :
y = 2^4 – 24(2^2) + 11
y = -69
For x = -2
y = (-2)^4 – 24(-2^2) + 11
y = -69
Result
So the points of inflection are (2, -69) and (-2, -69).
Graph
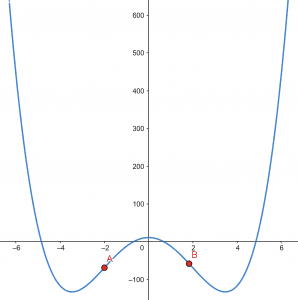
Figure 2
All the mathematical images/graphs are created using GeoGebra.
