JUMP TO TOPIC
Miller Indices Calculator + Online Solver With Free Steps
The Miller Indices Calculator is an online available widget used to determine the shape of the crystal and orientation of its plane in the crystal lattice. It is an easy-to-use calculator with a user-friendly layout that prompts the user to simply enter the value of indices and view the results.
The Miller Indices Calculator is used to observe the position and direction of the plane linked to the particular set of Miller indices that are denoted as H, K, and L.

What Is the Miller Indices Calculator?
The Miller Indices Calculator is a calculator that is used to visualize the arrangement and orientation of the internal plane of the crystal lattice that depends on the three indices generally called Miller indices.
The Miller Indices calculator uses the set of three Miller indices to identify the directions and positions of the planes of atoms in the crystal lattice. The calculator features the conception of particular planes in specified and peculiar crystal lattice structures such as cubic, body-centered cubic, etc. depending upon the defined Miller indices.
The position of the crystal plane of any crystal lattice is determined by the intersection of the plane with the crystallographic axes of the crystal structure or solid. The fractional intercepts of the three crystallographic axes (x, y, z) are defined as the miller indices which are used for identifying the particular crystal planes.
For instance, consider the cubic crystal structure shown in Figure 1:
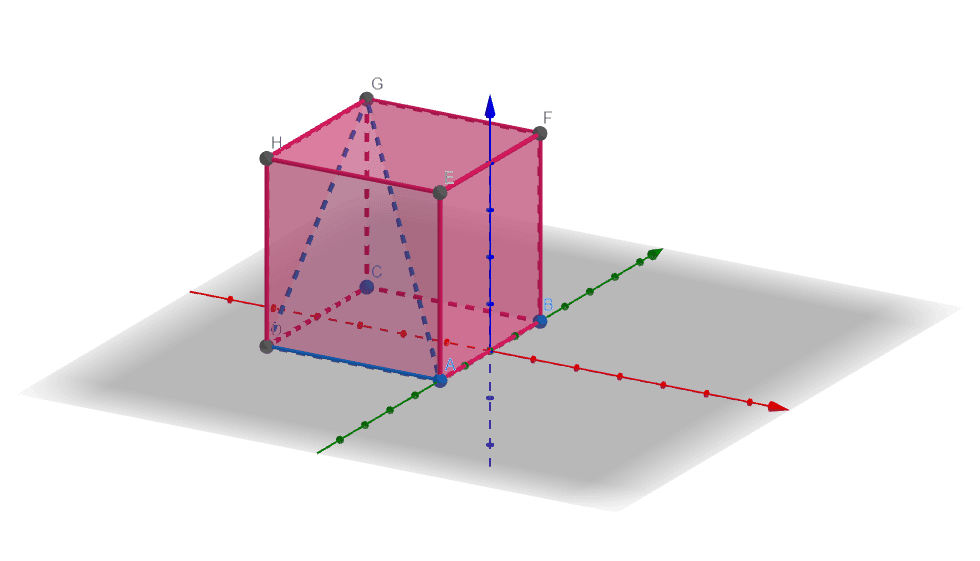
Figure 1
In this case, miller indices are given as:
H = 1
K = 1
L = 1
Therefore, this calculator produces clear visuals of the crystal plane associated with the values of Miller Indices.
How To Use the Miller Indices Calculator?
You can use the Miller Indices Calculator by entering the value of three miller indices into the appropriate blocks designed on the calculator and pressing the submit button.
The algorithm of this online calculator will make things easier for you and will instantly show you the orientation of the plane. You can get the desired results just in a second.
Here are the detailed stepwise instructions on how to use the miller indices calculator.
Step 1
First, calculate the value of Miller indices for the given crystal lattice.
Step 2
Input the values of three miller indices H, K, and L in the specified blocks on the calculator.
Step 3
After entering the required inputs, press the Submit button to view the result.
Step 4
The Result will appear in another window which shows the following two blocks:
Input Information
This block shows the data entered by the user which is the values of the Miller indices H, K, and L.
Corresponding Lattice Plane
This block shows the crystal plane of the solid related to specified miller indices.
How Does the Miller Indices Calculator Work?
The Miller Indices Calculator works by using the Miller indices to determine the position and direction of the crystal plane and creating the visualization of that plane in lattice structures.
To understand the working of the Miller Indices Calculator let’s just discover some important terms and techniques involved.
What Are Miller Indices?
Miller Indices are the three indices or numbers that define the orientation of the atomic plane of a solid crystal. Miller Indices can also be regarded as the notation system for the crystal planes in the crystal lattices. They are used to determine the shape of the lattice plane and the direction in which it is oriented.
Let’s figure out how to find the Miller indices. Here are some steps to be followed while determining the Miller indices:
- First, determine the point of intersection of the crystal plane with the crystallographic axes (x, y, z) concerning the dimensions of the unit cell.
- Now, take the reciprocal of the three intercepts which are x-intercept a, y-intercept b, and z-intercept c.
- Afterwards, clear the fraction to obtain the fractional intercepts.
- Make sure to reduce all the terms to the lowest form.
- The resulting numbers are the Miller indices.
The Miller indices are very useful for specifying the orientation and direction of the crystal planes and the atomic structures of the crystalline solids.
Solved Examples
Here are some examples solved using the Miller Indices calculator to visualize the crystal planes in the lattice structure.
Example 1
Determine the lattice structure and the orientation of the atomic plane.
The values of the miller indices are given as:
H = 1
K = 2
L = 1
Solution
Input the values of Miller indices in the specific blocks and press the submit button.
The corresponding lattice plane is shown in Figure 2 below:
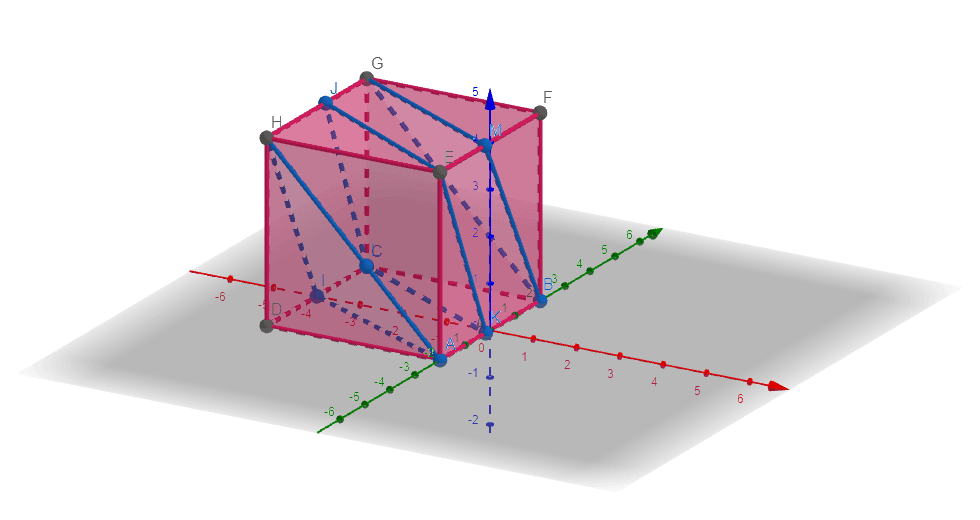
Figure 2
The specific lattice structure is Simple Cubic.
Example 2
Identify the orientation of the plane of a crystal lattice with the following Miller indices:
H = 1
K = 1
L = 0
Solution
The corresponding lattice plane for the given Miller indices is shown in Figure 3.
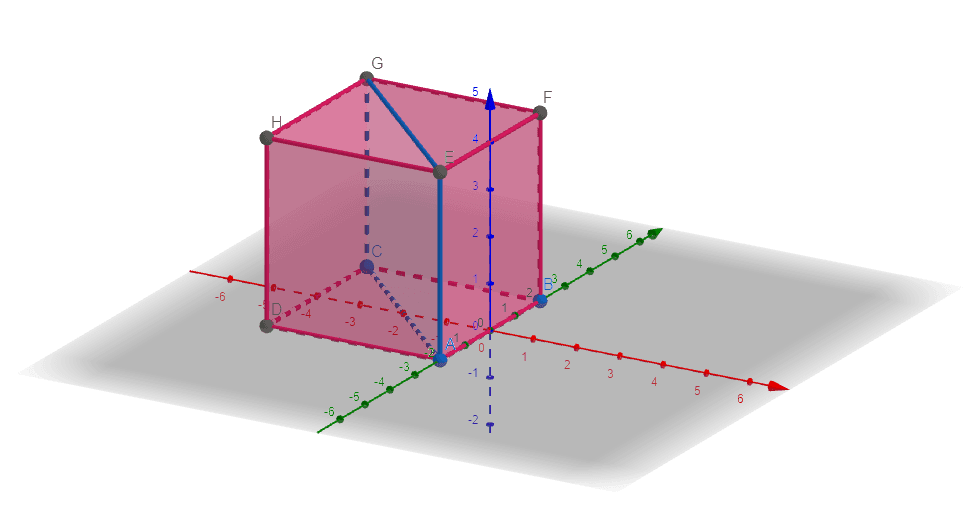
Figure 3
Therefore, the calculator can be used to determine the crystal planes.
All the images are created using GeoGebra.
