JUMP TO TOPIC
Mixture Problem Calculator + Online Solver With Free Steps
A Mixture Problem Calculator is a free tool that helps you find the quantities of different components in a mixture. The calculator takes the percentage of individual elements and the total mixture as input.
A mixture is a combination of two or more elements. The amount of the element can vary from one mixture to the other.
The calculator provides the mathematical equation for the mixture, exact values of the elements, alternate form for the equation, and graphs of the mathematical equations in the x-y plane.

What Is the Mixture Problem Calculator?
The Mixture Problem Calculator is an online calculator designed to determine the amount of each element in a mixture by using its percentage.
Mixtures are an essential element of life. For instance, the air is a mixture of several gases, seawater is a mixture of salt and water. Medicines are another classic example of a mixture. It means almost everything we observe is a mixture.
The mixtures are very significant in the fields of algebra and chemistry. The researchers by determining the portion of elements in each mixture discover its characteristics. This helps them to analyze and make new mixtures using various combinations.
The quantity of the element is determined by solving the mathematical equation of each mixture using different mathematical techniques. This method is a tedious task and also requires time to solve the problem.
Therefore, we provide you with an innovative tool that will efficiently solve your mixture problems known as Mixture Problem Calculator. It is easy to use as the calculator has a super-friendly interface.
How To Use the Mixture Problem Calculator?
You can use the Mixture Problem Calculator by entering equations for different mixtures. This calculator needs the mathematical equation and percentage of each element to solve the problem.
It can take values for up to three elements, the first two elements are components of the mixture and the last element is the resultant mixture itself.
To get the best results from the calculator you must follow every step written in the below section.
Step 1
Insert the mathematical equation for the mixture in the first row. This mathematical equation explains the relation between the mixture and components. For instance, a+b=c is mathematical equation of mixture c with its elements a and b.
Step 2
Now in the second row put the percentage of each element as a decimal. This percentage defines the portion of elements in the mixture. For example, the percentage equation is 0.5 a + 0.7 b = 1.2 c.
Step 3
Finally, click the Submit button to get the desired solution.
Result
The result is shown in multiple sections. The first section displays the input interpretation of the entered problem. It is a useful feature to allow users to check whether the calculator accurately reads their input or not.
Then it gives the accurate numerical values for each of the elements. After that, it provides a graph that plots both the general equation and percentage equation of the problem. Also, it provides two kinds of alternate forms.
The first alternate form is obtained by assuming that the quantities are the real numbers. While the second alternate form is a general form without any assumption.
How Does the Mixture Problem Calculator Work?
The calculator works by solving mathematical equations of the mixture using the substitution technique to get the values of components.
This calculator uses the percentage of the constituents to find the amount of each constituent. It can solve all types of mixture problems. We must cover a few key ideas to further understand how this calculator functions.
What Is a Mixture Problem?
Mixture problems are the problems that involve calculating the amount of each component of the mixture. Usually, mixture problems have two components and one resultant mixture. The quantity determined can be price, number, or percentage.
How To Solve Mixture Problems
You can solve the Mixture Problem by doing some simple steps. Let’s discuss them in detail with an example. For example, you want to mix 20% material and 30% another material to get 80% of the new solution.
The first step is to express the mixture in form of a mathematical equation. So for this example, we represent the first material by x, the second by y, and the final solution by z. So saline water can be represented as:
x + y = z
The second step is to express the same equation but with percentage as the coefficients with the variables. It can be written as a simple number or either in the form of decimals.
20x + 30y = 80z
The third step is the substitution method in which you represent one quantity in the form of other. For example, you represent x as:
x = z – y
Now using this value you put in the second equation to determine the value for variable y. The obtained value of y then can be used to get the value of x. This is how a simple technique solves the mixture problem.
Solved Examples
For understanding the working of the calculator, let’s discuss problems solved by Mixture Problem Calculator.
Example 1
A chemistry student needs to prepare 10 liters of 15% base solution by using the 10% and 30% base solutions for his experiment. To complete his experiment he now wants to calculate how much quantity of both available solutions he can use.
Solution
The calculator gives the following solution for the problem.
Input Interpretation
x1 + x2 = 10, 0.1 x1 + 0.3 x2 = 0.15 x 10
Equations
x1 + x2 = 10, 0.1 x1 + 0.3 x2 = 1.5
Values
x1 = 7.5 x2 = 2.5
Plots
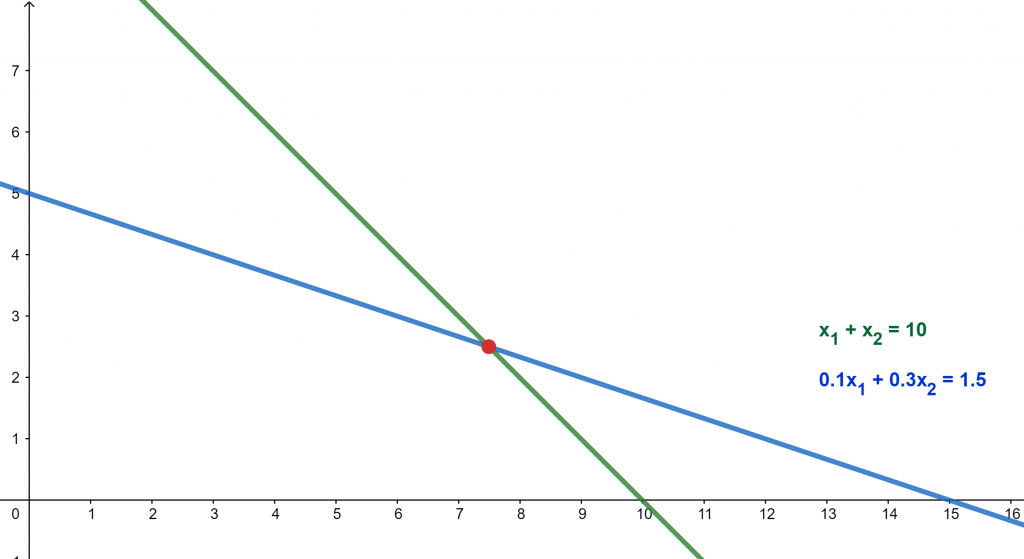
Figure 1
Alternate Forms
The alternate form assuming x1 and x2 are real is as follows:
x1 + x2 = 10, x1 + 3 x2 = 15
And,
x1 + x2 = 10, 0.1 x1 + 0.3 x2 + 0 = 1.5
Then the general alternate form is given as:
x1 + x2 = 10, x1 + 3 x2 = 15
x2 = 10 – x1, x2 = 5 – 0.333 x1
x1 + x2 = 10, 0.1 (x1 + 3 x2) = 1.5
Example 2
A civil engineer wants to build a flat. For this, he has to prepare 20 kgs of 95% concrete with the help of 45% cement and 20 % sand. Now he wants to calculate the amount for each material.
Input Interpretation
x + y = 20, 0.45 x + 0.2 y = 0.95 x 20
Equations
x + y = 20, 0.45 x + 0.2 y = 19
Values
x = 60, y = – 40
Plots
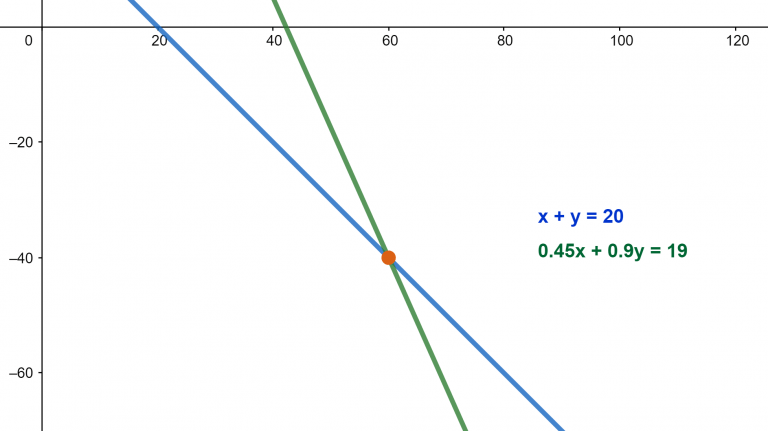
Figure 2
Alternate Forms
The alternate form assuming x and y are real is as follows:
x + y = 20, x + 0.444 y = 42.222
And,
x + y = 20, 0.45 x + 0.2 y + 0 = 19
The general alternate form is given as:
x + y = 20, x + 0.444 y = 42.222
y = 20 – x, y = 95 – 2.25 x
x + y = 20, 0.45 (x + 0.444 y) = 19
All the Mathematical Images/Graphs are created using GeoGebra.
