JUMP TO TOPIC
Mohr’s Circle Calculator + Online Solver With Free Steps
A Mohr’s Circle Calculator is a free tool that helps you to find different stress parameters of an object.
The calculator returns the mohr’s circle representation and minimum and maximum values of normal and shear stress as the output.
What Is the Mohr’s Circle Calculator?
The Mohr’s Circle Calculator is an online calculator that is designed to solve your problems involving plane stress using Mohr’s circle.
The concept of stress has a vast application in the field of physics, mechanics, and engineering. It can be used to determine the maximum pressure in a container, the extent of a stretch of an object and pressure of a fluid, etc.
Finding stress-related parameters is a difficult and hectic task. It requires a lot of time and computation for solving such problems. But this advanced tool can save you from the rigorous process.
This calculator is always accessible in your daily use browser without any installation.
How To Use the Mohr’s Circle Calculator?
You can use Mohr’s Circle Calculator by entering the parameters related to the plane stress problem in their respective boxes. The calculator’s interface is made simple so everyone can easily operate this tool.
The basic steps to use the calculator are given below.
Step 1
Insert the horizontal normal stress in the “X Direction” box and vertical normal stress in the “Y Direction” box.
Step 2
Now put the value of shear stress in the third field with the name “Shear Stress.” Also, insert the plane angle in its slot.
Step 3
Press the Submit button to get the final answer for the problem.
Result
The calculator’s result has multiple sections. The first section displays the shear stress in a new frame. The next section gives Mohr’s circle for the problem and also highlights the points of normal and shear stress.
The last section gives the average, maximum and minimum value of normal stress on the object. In addition to that, it also gives the maximum and minimum value of shear stress.
How Does the Mohr’s Circle Calculator Work?
The Mohr’s Circle Calculator works by drawing the mohr’s circle for the problem using the input elements. The circle has important parameters like shear and normal stress.
To better understand the functionality of the calculator we need to review some fundamental concepts.
Stress
Stress is a reactional force whenever an external force is applied to any surface area. It is equal in magnitude and opposite in direction to the applied force. The stress is represented as the force per unit area and its formula is as follows:
\[ S = \frac{F}{A} \]
The unit of stress is N/m$^\mathsf{2}$ or Pascal (Pa). There are two main types of stress which are Shear and Normal stress.
Normal Stress
When the force applied to an object is perpendicular to its surface area, then the resulting stress is called normal stress. Such stress can bring a change either in the length or volume of an object. The symbol of normal stress is ($\sigma$).
Shear Stress
The shear stress is a resultant force when an external force is applied to an object parallel to its surface area. This kind of stress can vary the shape of an object. The shear stress is denoted by the symbol ($\tau$).
Plane Stress
Plane stress means a condition in which stress along any particular axis is considered to be zero. It means that all stress forces acting on an object will exist on a singular plane.
Any three-dimensional object can have a maximum of three kinds of stress along the axes x, y, and z. Generally, both the normal and shear stress along the z-axis are assumed to be zero.
What Is the Mohr’s Circle?
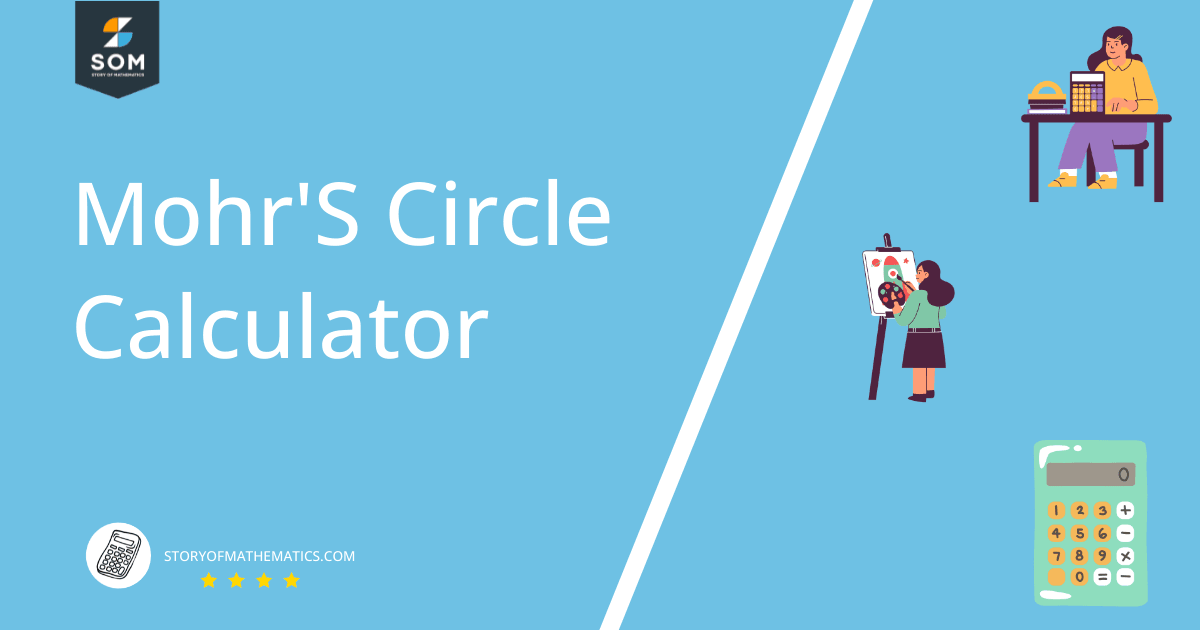
Mohr’s Circle is a method that uses graphical representation to determine the normal and shear stress acting on an object. The graph to plot mohr’s circle has normal stress on the horizontal axis and shear stress on the vertical axis.
The right side of the horizontal axis is the positive normal stress and the left side represents the negative normal stress.
On the other hand for shear stress, the upward side indicates negative and the lower side of the vertical axis represents positive stress.
Drawing Mohr’s Circle
Mohr’s circle is drawn in multiple steps on the normal-shear stress plane. The first step is to find the center of the circle, which is the average of two normal stress. It is written as:
\[ \sigma_{avg} = \frac{\sigma_{x} + \sigma_{y}}{2} \]
Then we plot two points, the first point ($\sigma_x,\, \tau_{xy}$) corresponds to stress on the x-face and the second point ($\sigma_y,\, -\tau_{xy}$). represents stress on the y-face of the object.
Now both points are joined together by a line passing through the center of the circle. This new line is the diameter of mohr’s circle which is used to draw the circle.
Each point on the circle represents normal and shear stress for different positions of the object. The radius of the circle is the maximum shear stress. It can be calculated as:
\[ R = \sqrt{\left(\frac{\sigma_{x} – \sigma_{y} }{2} \right)^2 + \tau_{xy}^2 } \]
Figure 1 shows the general form of mohr’s circle.
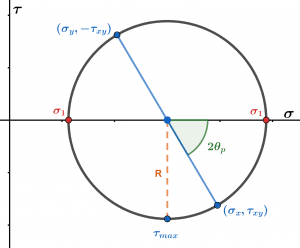
Figure 1
The shear stress will be zero at the points where the circle crosses the horizontal axis, at these points, we have maximum normal stress which is known as principal stress. To calculate them, the following formula is used.
\[ \sigma_{1,2} = \frac{\sigma_{x} + \sigma_{y}}{2} \pm \sqrt{ \left(\frac{\sigma_{x} – \sigma_{y} }{2}\right)^2 + \tau_{xy}^2 } \]
The angle between the stress element and the principal planes can also be determined by using the formula given below:
\[ \tan 2\theta_p = \frac{\tau_{xy}}{(\sigma_{x}-\sigma_{y}) \, / \, 2} \]
Solved Examples
Some of the problems solved using the calculator are explained below.
Example 1
Consider a stress element with the following characteristics:
\[ \sigma_{x} = -8 \text{ MPa}, \, \sigma_{y} = 12 \text{ MPa}, \, \tau_{xy} = 6 \text{ MPa} \]
Determine the principal and shear stresses using Mohr’s circle.
Solution
The answer provided by the calculator is given as:
Shear Stress
It gives the value of shear stress in the new frame.
\[ \text{Shear stress} = 6 \text{ MPa} = 870.2 \text{ psi} = 6 \times 10^{6} \text{ Pa} \]
Schematic
Mohr’s circle representation is given in figure 2.
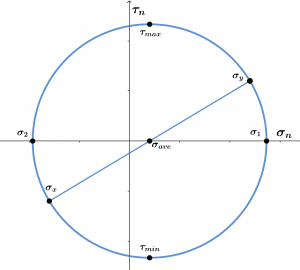
Figure 2
Mohr’s Circle Parameter
The fundamental parameters of mohr’s circle are:
\[ \text{Average Normal Stress} = 10 \text{ MPa},\: 1450 \text{ psi},\: 1 \times 10^{7} \text{ Pa} \]
\[ \text{Maximum Normal Stress} = 35.71 \text{ MPa},\: 5179 \text{ psi},\: 3.571 \times 10^{7} \text{ Pa} \]
\[ \text{Minimum Normal Stress} = -15.71 \text{ MPa},\: -2279 \text{ psi},\: -1.571 \times 10^{7} \text{ Pa} \]
\[ \text{Maximum Shear Stress} = 25.71 \text{ MPa},\: 3729 \text{ psi},\: 2.571 \times 10^{7} \text{ Pa} \]
\[ \text{Minimum Shear Stress} = -25.71 \text{ MPa},\: -3729 \text{ psi},\: -2.571 \times 10^{7} \text{ Pa} \]
Example 2
A stress element has the following forces acting on it.
\[ \sigma_{x} = 16 \text{ MPa}, \, \sigma_{y} = 4 \text{ MPa}, \, \tau_{xy} = 25 \text{ MPa} \]
Draw Mohr’s circle for the element with angle $\theta_{p} = 30^{\circ}$.
Solution
Shear Stress
\[ \text{Shear stress} = 7.304 \text{ MPa} = 1059 \text{ psi} = 7.304 \times 10^{6} \text{ Pa} \]
Schematic
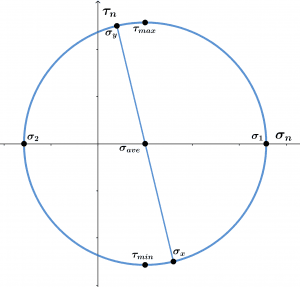
Figure 3
Mohr’s Circle Parameter
\[ \text{Average Normal Stress} = 2 \text{ MPa},\: 290.1 \text{ psi},\: 2 \times 10^{6} \text{ Pa} \]
\[ \text{Maximum Normal Stress} = 13.66 \text{ MPa},\: 1981 \text{ psi},\: 1.366 \times 10^{7} \text{ Pa} \]
\[ \text{Minimum Normal Stress} = -9.66 \text{ MPa}, \:-1401 \text{ psi},\: -9.66 \times 10^{6} \text{ Pa} \]
\[ \text{Maximum Shear Stress} = 11.66 \text{ MPa},\: 1691 \text{ psi},\: 1.166 \times 10^{7} \text{ Pa} \]
\[ \text{Minimum Shear Stress} = -11.66 \text{ MPa},\: -1691 \text{ psi},\: -1.166 \times 10^{7} \text{ Pa} \]
All the Mathematical Images/Graphs are created using GeoGebra.
