JUMP TO TOPIC
Polar Derivative Calculator + Online Solver With Free Steps
The Polar Derivative Calculator is used to accurately determine the derivatives of polar functions. The polar functions are based on the system of polar coordinates.
This calculator takes the function and the angle input from the user and calculates the polar derivative.
The Polar Derivative Calculator is a free tool that provides efficient answers. It displays the solution in two forms: mathematical form and graphical form.

What Is a Polar Derivative Calculator?
The Polar Derivative Calculator is an online tool that is used to calculate the derivative of the given polar functions.
These polar functions are defined as:
r = f($\theta$)
The Polar Derivative Calculator computes the polar derivative depending upon the polar function and the specified angle in polar coordinates system. The calculation of such derivatives is slightly different than the conventional derivatives. The Polar Derivative Calculator makes use of the following formula for the calculation of polar derivatives:
\[ \frac{dy}{dx} = \frac{\frac{dr}{d\theta} sin\theta + rcos\theta}{\frac{dr}{d\theta} cos\theta – rsin\theta} \]
How To Use the Polar Derivative Calculator?
You can use the Polar Derivative calculator by directly entering the polar equation and related angle in radians to compute the polar derivative. The Polar Derivative Calculator is extremely easy to use due to its simple user-friendly interface. This calculator has two input boxes, one box is for the equation and the other is for angle.
Here is a step-by-step guide for using this calculator.
Step 1
First, analyze the polar function and the angle for which you want to calculate the polar derivative. Make sure that the angle you use is in radians.
Step 2
After you have analyzed your function, insert the polar function in the box titled “Equation.” Similarly, enter your angle in the box titled “Angle (radians).”
Step 3
Once you have entered the input values, click on the button that says “Submit.” The solution will begin to load.
Step 4
You will get the solution in two forms — mathematical and graphical. You will also get the slope of the tangent line in the solution.
Solved Example
To enhance your concept regarding the polar derivative calculator, given below is a solved example.
Example 1
Find the polar derivative of the following function at $\frac{\pi}{2}$. The function is given below:
r = 2 sin $\theta$
Solution
As the first step, analyze the polar function and make sure that the angle given is in radians. After that, simply insert the input parameters into the calculator.
In the first input box, enter the following polar function:
r = 2 sin $\theta$
In the second input box, enter the angle in radians:
\[ \frac{\pi}{2} \]
Now simply click on “Submit” to obtain the solution. The calculator makes use of the following formula for obtaining the solution of the polar derivative:
\[ \frac{dy}{dx} = \frac{\frac{dr}{d\theta} sin\theta + rcos\theta}{\frac{dr}{d\theta} cos\theta – rsin\theta} \]
The answer obtained is:
Polar Derivative = 0
The slope of the tangent line is given as:
y =2
The calculator also provides the following graphical solution shown in Figure 1:
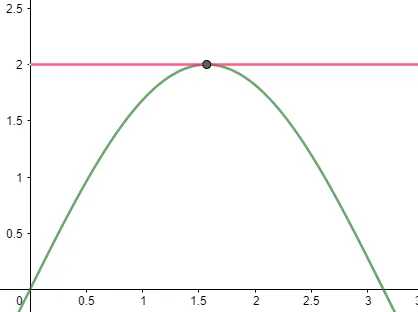
Figure 1
All Mathematical Images/Graphs are created using GeoGebra.
