JUMP TO TOPIC
Polygon Calculator + Online Solver With Free Steps
The online Polygon Calculator is a free tool that allows you to find the properties of any polygon. Polygons are shapes that have three or more sides.
The calculator requires the number of sides and the side length to create and extract the characteristics of the polygon.

What Is the Polygon Calculator?
The Polygon Calculator is an online calculator specifically designed to determine the polygon’s detailed properties and characteristics.
Polygons are one of the fundamental shapes in geometry. If one wants to determine the properties of these shapes, there are specific formulas used to calculate each of the properties.
Also, when the shape varies, the formula for each of the properties changes. For example, the heptagon and pentagon both have different formulas for area.
So you have to perform a massive rock of calculations repeatedly, which is a tedious and tiring task. But you can save time using the Polygon Calculator because it finds all necessary properties in less than a second.
How To Use the Polygon Calculator?
To use the Polygon Calculator, we simply plug in the number of sides and the side length of the polygon in the given boxes. The step-by-step guidelines on the use of the calculator are given below.
Step 1
First, insert the number of sides for your polygon in the first tab.
Step 2
Then put the value for the length of the sides of the polygon in the second tab.
Step 3
Now you can click on the ‘Submit’ to get the results.
Output
The calculator’s output consists of multiple sections. The first section shows the name of the shape and the side length provided as input by the user. The second section is a table containing nine different polygon properties.
Then it provides a visual representation of the polygon with its possible diagonals. At last, there is a table describing the polygon’s characteristics.
How Does the Polygon Calculator Work?
The polygon calculator works by finding the name, properties, and diagonals of the given polygon and providing the properties.
It inputs the number of the sides of the polygon and the side length, and as a result, it provides the polygon shape along with its properties such as area, perimeters, height, etc.
This calculator is useless without knowing about the polygons and their properties, so let’s discuss the polygons and their properties.
What Is a Polygon?
A polygon is a closed two-dimensional shape formed by three straight lines. The word “Polygon” is a greek word that means “many angles.” The polygons are classified based on their number of sides, properties, and structures.
A polygon can be identified by its characteristics which include that a polygon can not be a three-dimensional shape, it does not have any curved surfaces, and always a plane shape.
It should have more than two sides and is always in a closed shape, meaning there is no open side.
Types of Polygons
The polygons are divided into two main types based on their side length and angles. The two types are Regular polygons and Irregular polygons.
Regular polygons have equal side lengths and equal measurements of their interior and exterior angles. These convex polygons mean all interior angles are less than 180 degrees.
This calculator determines the shape and properties of Regular polygons.
The polygons whose side lengths are not equal and have unequal measurements of their exterior and interior angles at each vertex are called Irregular polygons.
Names of Polygons
The number of polygons’ sides determines the polygon’s name and shape. The shapes of the polygons, along with their number of sides, are given below:
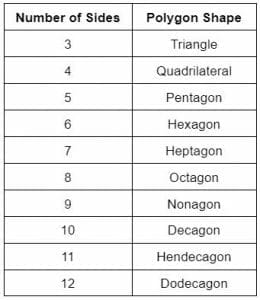
Table 1
In the same manner, as the number of sides of polygons increases, it results in a new polygon shape.
Properties of the Polygon
The polygon’s properties include its area, perimeter, angles, circumradius, and apothem. The properties of only the regular polygon are discussed below since this calculator only finds the properties of the regular polygon.
Area
The area that is surrounded by the boundary of a polygon is the area of a polygon. The space inhabited by the polygon in a two-dimensional plane can also define its area.
The following formula calculates the area of a regular polygon:
Area = 1/2 (number of sides * length of one side* apothem)
Where apothem is given by $\dfrac{l}{2 tan(180/n)}$.
Perimeter
The perimeter of a polygon is determined by taking the sum of the length of all sides of the polygon. It is also present in a two-dimensional plane. The formula to calculate the perimeter of any regular polygon is given as follows:
Perimeter = (number of sides) * (side length)
Angles of Polygon
The angles in a polygon are of two types that are interior angles and exterior angles. Those angles formed between the adjacent sides of a polygon are considered interior angles.
These angles are equal to the number of the sides of a polygon. The following formula is used to find the value of interior angles.
Interior angle = $\dfrac{180^\circ-(n-2)}{n}$
Where ‘n’ is the number of sides of the polygon.
The angle that is formed by extending any side of the polygon is known as the exterior angle of a polygon. The sum of all exterior angles is equal to 360 degrees. The value of the exterior angle is given by:
Exterior angle = $\dfrac{360^\circ}{n}$
Apothem
The line drawn from the polygon’s center to the midpoint of any side is called an apothem. The following formula calculates the length of the apothem:
a = $\dfrac{l}{2 tan(180/n)}$
Solved Examples
Let’s have a look at a few solved problems via the Polygon Calculator.
Example 1
A math student is given a polygon with five sides; its side length is 2 cm. He is asked to find the properties of the resultant polygon in an exam.
Solution
The calculator provides the solution as follows.
Properties
The polygon is a regular pentagon, and its characteristics are given below:
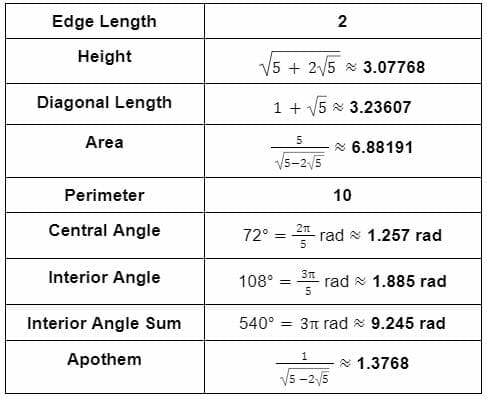
Table 2
Diagonals
The pentagon and its diagonals are shown in figure 1 below.
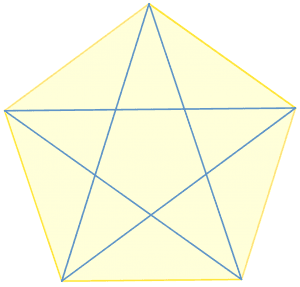
Figure 1
Some characteristics of the polygon are provided in Table 3.
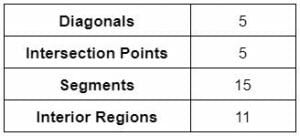
Table 3
Example 2
Consider a polygon with seven sides, and the length of each side is 4 cm. Find out the properties and number of diagonals in this polygon.
Solution
Properties
Table 4 shows the properties of the heptagon in detail.
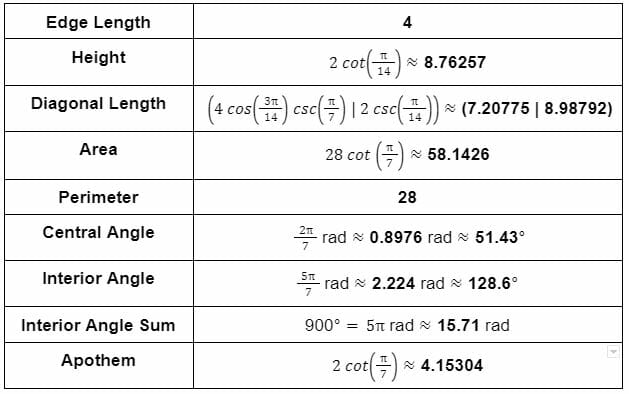
Table 4
Diagonals
Figure 2 illustrates the obtained heptagon with the diagonals highlighted in blue color.
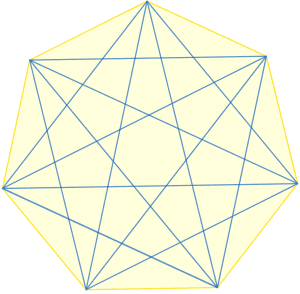
Figure 2
The heptagon has the following characteristics.
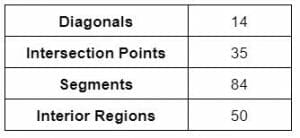
Table 5
