JUMP TO TOPIC
Power Series Calculator + Online Solver With Free Steps
The Power Series Calculator is an online tool that determines the power series for a mathematical function having one variable. The calculator can take in input details regarding the function and the point around which it evaluates power series.
Power Series is an expression with an infinite number of terms where each term has a coefficient and variable with some power. The degree of power series is also infinite as there is no fixed highest degree for the variable.
This tool outputs the power series of the given function, plots the graph of initial terms, and provides a general representation of the power series.

What Is a Power Series Calculator?
A Power Series Calculator is an online calculator which you can use to compute power series about a central point for your mathematical functions.
In the field of finance and mathematics, functions are frequently represented as power series as it helps to simplify the problem. It approximates functions around a certain point, which makes the definite integrals easy to solve.
Also, it helps to derive formulas, evaluate limits and reduce the complexity of a complicated function by eliminating insignificant terms. The point of convergence of power series plays an important role in manipulating the problems.
It is a very tedious task to find and plot power series for any function. Solving it by hand demands a lot of computation. That’s why we have this advanced calculator which solves calculus problems like power series for you in real-time.
How To Use the Power Series Calculator?
You can use the Power Series Calculator by plugging in a valid mathematical function and pivot point in their respective fields. By pressing a single button, results will be presented in a few seconds.
Follow the guidelines on how to use the Power Series Calculator given in the below section:
Step 1
First, put your function in the Power Series For box. It should be a function of only one variable x.
Step 2
Then enter the central point in the field with the name About A. This is the about which the power series is calculated.
Step 3
At the last, click the Solve button to get the entire solution to the problem.
An interesting fact about this calculator is that it can be used for a variety of functions. The function can be exponential, trigonometric and algebraic, etc. This excellent feature increases its value and makes it more reliable.
Result
The solution is provided in different portions. It starts with presenting the input interpretation made by the calculator. Then it displays the series expansion with some starting terms. These terms can vary if the central point is changed.
It also provides the graph of these starting terms about the central point in the approximation part. Then it gives the general form of the obtained power series in the form of a summation equation.
How Does the Power Series Calculator Work?
The power series calculator works by expanding the given function as a power series centered around the given value of a. It also gives the Taylor Series expansion of the function if it is differentiable.
But the question is what is the power series and its significance in mathematics? The answer to this question is explained below.
What Is the Power Series?
Power Series is a function with infinitely many terms in the form of the polynomial. It contains the terms involving variables, hence it is a special type of series. For instance, if there is a variable x, then all the terms involve the powers of x.
Power series expands the common functions or can define new functions also. A power series centered at x=a in summation is given as:
\[\displaystyle\sum_{n=0} ^{\infty} c^n (x-a)^n= c_0+c_1(x-a)+c_2(x-a)^2+….+c_n(x-a)^n\]
Where x is the variable and $c_n$ are the coefficients.
Order of the Power Series
The order of the power series is equal to the lowest power of the variable with a non-zero coefficient. This means that the order of the series is the same as the order of the first variable. If the first variable is quadratic then the order of the series is two.
Convergence of Power Series
Power Series contains infinitely many terms involving variable x but it will converge for certain values of the variable. By convergence, we mean that the series has a finite value. However, the series may diverge also for other values of the variable.
A Power Series always converges at its center which means that the sum of the series is equal to some constant. Hence it will converge for that value of variable x for which the series is centered at.
However, many power series converge for more than one value of its variable x such as it can converge either for all the real values of variable x or for a finite interval of x.
If the power series which is given by $ \displaystyle\sum_{n=0} ^{\infty} c^n (x-a)^n $ converges at center a, then it should satisfy any one of the following conditions:
- For all the values of x=a, the series converges and it diverges for all the values of $x\neq a$.
- The series converges for all the real values of x.
- For a real number R>0, the series converges if |x-a|<R and diverges for |x-a|>R. However, if |x-a|=R then the series may converge or diverge.
Interval of Convergence
The set of all values of variable $x$ for which the given series converges at its center is called the Interval of Convergence. This means that the series will not converge for all the values of $x$ rather it only converges for the specified interval.
Radius of Convergence
The power series converges if |x-a|<R for a real number R>0 where R is called the radius of convergence. If the series does not converge for a specified interval but it converges for only one value at x=a, then the radius of convergence is zero.
And if the series converges for all real values of variable x, then the radius of convergence is infinite. The radius of convergence is half of the interval of convergence.
The interval of convergence and radius of convergence is determined by applying the ratio test.
Ratio Test
The ratio test is mostly used to find the interval and radius of convergence. This test is given by:
\[L= \lim_{n\to\infty} \frac{|a_{n+1}|}{|a_n|} \]
Depending on the result of the above ratio test, three conclusions can be drawn.
- If L<1, then the series will converge absolutely.
- If L>1 or L is infinite, then the series will diverge.
- If L=1, then the test is indecisive.
Now if the ratio test is equal to L<1, then by finding the value of L and putting it to L<1 we can find all the values in the interval for which the series converges.
The radius of convergence R is given by |x-a|<R. The interval of convergence is defined by a-R<x<a+R, where a is the center of the power series.
Representing Functions as Power Series
The power series is used to represent the function as a series of infinite polynomials. Polynomials are easy to analyze because it contains fundamental arithmetic operations.
Moreover, we can easily differentiate and integrate complicated functions by representing them in power series. This calculator represents the given function by a power series. The most important power series is the Geometric series, Taylor series, and Maclaurin series.
Geometric Series
The geometric series is the sum of the finite or infinite terms of the geometric sequence. A geometric sequence is a sequence where the ratio of two consecutive terms is constant. The geometric series can be finite or infinite.
The finite geometric series is given as:
\[a+ar^2+ar^3+…+ar^{n-1}\]
And the sum of this series is as follows:
\[\frac{a(1-r^n)}{1-r}, \:when \: r\neq 1\]
Where $r$ is the common ratio.
The infinite geometric series can be written as:
\[a+ar^2+ar^3+……..\]
The sum of this infinite series is calculated by
\[\frac{a}{1-r}, \:when \: r< 1\]
The complicated function can be represented by geometric series to analyze more easily.
Taylor Series
Taylor series is an infinite sum of the terms which are expressed as derivatives of a given function. This series is useful because it expands the function using the derivatives of the function at a value where the series is centered at.
The Taylor series is represented as follows:
\[\displaystyle\sum_{n=0} ^{\infty} \frac{f^n(a)}{n!}(x-a)^n= f(a)+\frac{f^1(a)}{1!}(x-a)+\frac{f^2(a)}{2!}(x-a)^2+…+\frac{f^n(a)}{n!}(x-a)^n\]
Where f(x) is a real-valued function, a is the center of the series means the given series is centered about a.
Maclaurin Series
Maclaurin Series is a special type of Taylor series where the center of the series is at zero. It means that when center a=0, we get the Maclaurin Series.
Solved Examples
There are some problems solved using Power Series Calculator explained in detail below.
Example 1
Let the below given algebraic function as the target function.
\[ f(x) = \frac{3}{5-x} \]
and
a = -2
Compute the power series for the function about point a.
Solution
Power Series
The power series expansion for the function is given as:
\[ \frac{3}{7} + \frac{3(x+2}{49} + \frac{3(x+2)^2}{343} + \frac{3(x+2)^3}{2401} + \frac{3(x+2)^4}{16807} + \frac{3(x+2)^5}{117649} + O\left( (x+2)^6 \right) \]
converges when |x+2| < 7
The initial terms are written whereas the rest of the terms up till point $n$ are represented by O.
Graph
The approximations of the series at x = -2 are illustrated in figure 1. Some terms are represented by a straight line while the other terms with dotted lines.
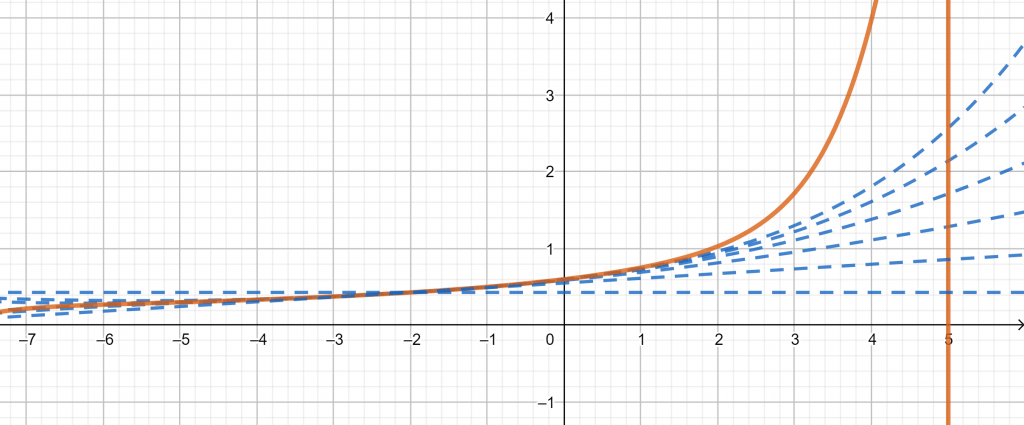
Figure 1
General Representation
The general form to represent the series is as follows:
\[ \sum_{n\ge0} 3\times7^{-1-n} (2+x)^n \]
Example 2
Consider the below algebraic function.
\[ f(x) = \frac{1}{1-x^2} \]
and
a = 0
Use the Power Series Calculator to get the series of the above function.
Solution
Power Series
The power series expansion of input function is as follows:
\[ 1 + x^2 + x^4 + O(x^6) \]
converges when x = 0
The higher-order terms are represented by O.
Graph
Figure 2 demonstrates the approximations of the series at x = 0.
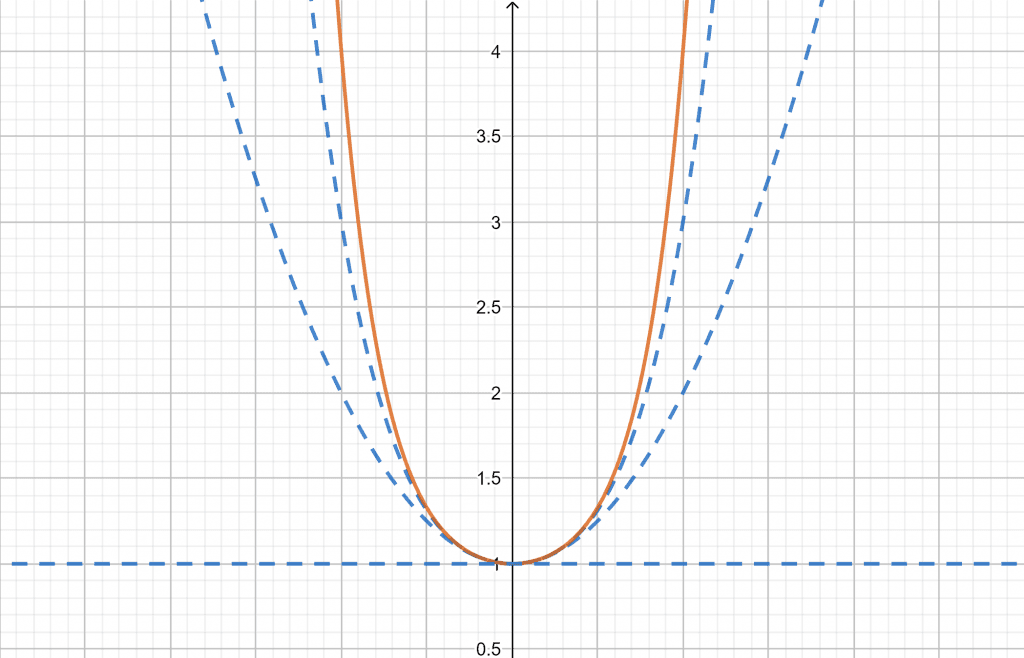
Figure 2
General Representation
The general form to represent this series is given below:
\[ \frac{1}{1-x^2} = \sum_{n=0}^{\infty} \frac{1}{2} x^{n} \left( 1+ (-1)^n \right) \]
\begin{align*}
\frac{1}{1-x^2} = \sum_{n=-\infty}^{\infty} \left(\begin{array}{lr}
-\frac{1}{2} & n = -1\\
(-1)^n\,2^{-2-n} & n \ge 0
\end{array}
\right)(-1 + x)^n
\end{align*}
All the Mathematical Images/Graphs are created using GeoGebra.
