JUMP TO TOPIC
Quadratic Formula Calculator + Online Solver With Free Steps
The Quadratic Formula Calculator is a free tool used to solve standard quadratic equations using the quadratic formula. Quadratic equations are the equations in which the highest degree of variable is two.
The quadratic formula is one of the most widely used methods to solve quadratic equations. It utilizes the coefficients of the equation to evaluate the roots.
This calculator determines the roots of quadratic equations. In addition to that, it gives the graph of equations and also plots the roots in the plane of the unknown variable.

What Is the Quadratic Formula Calculator?
The Quadratic Equation Calculator is an online tool that is used to calculate the roots and graph of any complex quadratic equation without any hassle.
The quadratic equation is a second order equation. As the degree of the equation is two, there are only two possible roots that can satisfy the equation. If the degree of the variable is greater than two, then they are called higher-order polynomials.
To solve the quadratic equation, there are many techniques but the most feasible one is the Quadratic formula. Because in the field of mathematics, all the quadratic equations can be solved with this single formula.
You can solve these equations by hand using the quadratic formula, but when the equations get complicated, especially when the coefficients are relatively bigger or the roots appear to be of a complex type, then solving such equations by hand is a nightmare for students. But don’t worry, this online widget has got you covered.
To plot the quadratic equations is another frustrating and time-intensive procedure. You need to insert different values individually in the quadratic equation and find the value of the function for the graphical demonstration. Then the resultant values are connected to get the final shape.
Therefore, you need a tool that can solve the equations quickly, irrespective of the complexity of the roots and equations. Also, a graphical visualizer is of great help for determining the shape of graphs for the given functions.
One such calculator with both the required features is the Quadratic Formula Calculator. It is not an application that needs to be installed on your device. You can run this tool easily in your daily use browser.
The quadratic equation is the backbone of many physical and engineering models. That’s why it’s very important to solve such equations precisely and efficiently.
How To Use the Quadratic Formula Calculator?
You can use the Quadratic Formula Calculator by entering the coefficients of all the terms of the equation in the specified fields on the calculator. The operation of this calculator is fairly easy and the interface is user-friendly.
The calculator is extremely reliable as it returns error-free results in a couple of seconds. The interface consists of three input boxes for the coefficients of each term of the quadratic equation. Also, there is a button used to process the equation.
The Quadratic Formula Calculator is one of the best tools to obtain the values for the quadratic equations. Once you have a standard quadratic equation, the detailed steps to use the calculator are as follows:
Step 1
First, ensure that the input equation is in standard form. Put the coefficient of the first term in the $x^2$ box.
Step 2
Then enter the coefficient of the second term in the x tab. These two terms are related to the variable portion of the function.
Step 3
Now insert the constant term in the last tab. After inserting all the elements, click the Submit button to obtain the solution.
Result
The result is demonstrated in three parts. First, it provides an x-y graph of the input equation with the highlighted location of roots.
Second, it plots the same roots in a single plane of the respective variable. Third, it displays the numerical values for the two actual roots of the quadratic equation.
How Does the Quadratic Formula Calculator Work?
The Quadratic Formula calculator works by finding the roots of a quadratic equation using the Quadratic Formula.
The Quadratic Formula is given as:
\[x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\]
The roots of the equation are solutions for which equality is satisfied.
Since it is a Quadratic Equation, therefore it has two roots. The nature of these roots depends on the value of the Discriminant. The expression $b^2-4ac$ in the Quadratic formula is called the discriminant.
This value can be zero, positive, or negative, which decides the nature of the roots.
Nature of the Roots
There are different cases for discriminant, which are explained below.
Case 1 ($b^2 – 4ac$ > 0)
When the value of the discriminant is positive, then the roots of the equation are real and unequal. For example, a and b are two roots such that $a\neq b$.
Case 2 ($b^2 – 4ac$ < 0)
When the discriminant value is negative, the roots are imaginary and unequal such as one root is ai and the other root is bi.
Case 3 ($b^2-4ac$ = 0)
When the discriminant is equal to zero, in this case, the roots are real and equal. For instance, both roots are equal such that a=b.
Case 4 ($b^2 – 4ac$ > 0 and perfect square)
When the value is positive and also a perfect square, then the solution of the equation is real, unequal, and rational numbers. This includes roots such as $\frac{a}{b}$ and $\frac{c}{d}$
Case 5 ($b^2 – 4ac$ > 0 and not perfect square)
When the value is positive but not a perfect square, then the solution is real, unequal, and irrational numbers. This includes roots such as $\sqrt{2}$ and $\sqrt{7}$.
Graphical Representation of the Roots
Here are some graphical interpretations showcasing what the graph looks like as the roots change.
Case 1
The roots are real and unequal when the discriminant value is positive. It is represented graphically as shown in Figure 1:
The parabola cut the x-axis at two distinct points, resulting in accurate and unequal solutions.
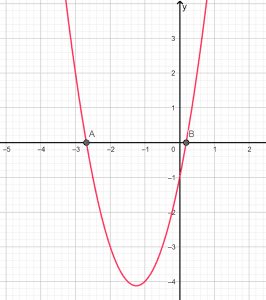
Figure 1
Case 2
The roots are imaginary and unequal since the discriminant is negative. The graphical representation is given below in Figure 2:
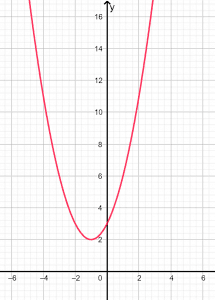
Figure 2
In the above graph, we can see that the parabola does not cut the x-axis at any point, therefore the roots are imaginary.
Case 3
When the discriminant is equal to zero, the roots are real and equal. It can be shown in a cartesian plane as in Figure 3:
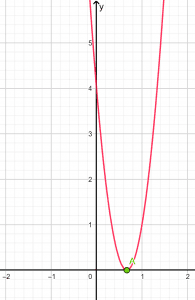
Figure 3
The parabola intersects the x-axis at only one point, which shows that the roots are real and equal.
Applications of Quadratic Equations
The quadratic equations are used in most mathematical problems. Quadratic equations can be used for solving many real-world problems, for area calculations, for an object moving in projectile motion, for for-profit and loss calculations, and for finding the speed of an object, optimization function, etc.
Now we will see some real-life applications that will help you to clear your concepts further.
Problem 1
You need to make a study table whose length is two meters more than its breadth. You have been provided with three meters square of wood. What will be the dimension of the table with the available wood?
Solution
The length of the table is 2 meters more than its width.
As we know, the formula for Area is written as:
(Length)(Breadth)= Area
(x+2)(x)= 3
\[x^2+2x-3=0\]
Here a=1, b=2 and c=3. Putting these values in the quadratic formula.
\[x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\]
After using the quadratic formula, you will get the values x=(1,3).
Problem 2
A man purchased onions for x dollars and sold them for 10 dollars. If he roughly estimates his loss percent at x%, what is the cost price of coins (x)?
Solution
Using the below-mentioned Loss percent Formula:
\[Loss Percent=\frac{Loss}{Cost \:Price}100\]
\[ x = (\frac{x-10}{x})100 \]
\[x^2=100x-100\]
\[x^2 – 100x+100=0\]
So the coefficients are a=1, b=-100, and c=1000. Now enter these values in the quadratic formula.
\[x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\]
After using the quadratic formula, you will get the values for x, which are 11.2 and 88.7.
Quadratic Formula To Find Roots
The quadratic formula is one of the most popular formulas in mathematics. This popularity is due to fact that it can solve several quadratic equations, which is rather a very tedious task if solved through the factorization technique.
For using the quadratic formula to determine the roots, the quadratic equation must be written in its standard form. The standard form is given as:
\[ ax^2 + bx + c = 0 ; \; a\neq0\ , b\neq0\ , c\neq0 \]
The quadratic formula is given as:
\[x= \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]
In the above formula, $a$ donates the coefficient of $x^2$, b donates the coefficient of x, and c is constant. To solve the equation, just plug in the values in the formula and we will have the required solution.
There are other methods that can be used to solve quadratic equations, but this formula method is mostly used due to its simplicity.
Deriving Quadratic Formula
The derivation of the Quadratic Formula from the standard form of a quadratic equation is explained below in detailed steps.
As we know, the standard form of a quadratic equation is as follows:
\[ ax^2 + bx + c = 0 \]
Step 1
Divide the standard quadratic equation. The right side will remain zero and the expression will look like this:
\[ x^2 + \frac{b x}{a} + \frac{c}{a} = 0 \]
Step 2
On both sides of the equation, add $-\frac{c}{a}$ to prepare for completing the square method.
\[ x^2 + \frac{b x}{a} = – \frac{c}{a}\]
Step 3
Also add $(\frac{b}{2a})^2$ on both sides to complete the square.
\[ x^2 + \frac{b x}{a} +(\frac{b}{2a})^2= – \frac{c}{a}+ (\frac{b}{2a})^2 \]
Step 4
Now the left side of the equation is the square of a binomial.
\[ (x +\frac{b}{2a})^2= – \frac{c}{a}+ \frac{b^2}{4a^2} \]
Step 5
Find a denominator for the addition of two fractions on the right side of the equation.
\[ (x +\frac{b}{2a})^2= – \frac{4ac}{4a^2}+ \frac{b^2}{4a^2} \]
Step 6
Add both fractions on the right side of the equation.
\[ (x +\frac{b}{2a})^2= \frac{b^2-4ac}{4a^2} \]
Step 7
Now take the square root of both sides of the equation.
\[ x +\frac{b}{2a}= \pm\frac{\sqrt{b^2-4ac}}{2a} \]
Step 8
Now add -$\frac{b}{2a}$ on both sides of the equation.
\[ x = -\frac{b}{2a} \pm\frac{\sqrt{b^2-4ac}}{2a} \]
Step 9
Add both fractions and you will get the Quadratic Formula.
\[x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\]
This is known as the Quadratic Formula. It applies to all types of quadratic equations, and it is used for finding the solution to quadratic equations. There are also other methods for finding the solutions to quadratic equations like the factorization method and completing squares method, etc.
History of Quadratic Formula
Quadratic Formulas have an interesting history and in ancient times, different types of quadratic formulas were used. The problem of finding the solution to a simple quadratic equation was first encountered by both Babylonians and Egyptians and then by the Greeks and Chinese.
While calculating areas and dimensions of plots problems occurred in quantities involving the square of quantities, Egyptians were using descriptive methods that were hard to follow. Instead of driving the formula, they noted the areas of different squares and developed a table of values.
Babylonians were the next to face the same problem. They tried to find formulas for the calculation of areas of different shapes. So they derived a complete square method for solving their problems involving areas. Babylonians were the only ones using a number system at that time.
Ancient Greeks and Chinese were also trying to solve these problems. At that time the concept of Algebra and Algebraic terms were not yet developed, so they were working to solve these problems geometrically. The Chinese were doing their mathematics using Abacus.
Then in the 9th century, a Persian scientist Muhammad bin Musa al-Khwarizmi, known as the father of algebra, introduced algebra and used symbols and the concept of equations. He first created a method to solve quadratic equations, but this method was only for positive values.
A European mathematician Girolamo Cardano combined al-Khwarizmi’s algebraic approach and the geometric approach together and he figured out how to solve these quadratic equations that will be for all values even for imaginary numbers as well.
Simon Stevin in 1594 introduced a quadratic formula that was covering all cases. The quadratic formula that we are using today was introduced by Rene Descartes in 1937; it contains all special cases of the quadratic formula.
Solved Examples
A good way to understand the tool is to solve the examples using it and analyze those examples. Some of the examples are discussed below to enhance your understanding and comprehension. The examples are solved using this calculator.
Example 1
Consider the following quadratic equation:
\[ x^2 – 3x +4 = 0 \]
Find the roots of the equation using the quadratic formula.
Solution
Root Plot
The x-y graph for the above equation is given in Figure 4. The resultant is a parabola facing upward with a global minimum above the x-axis.
The root plot is shown as:
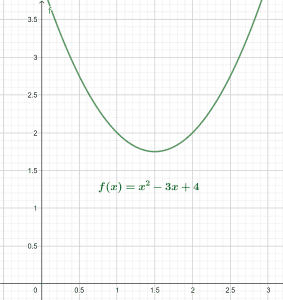
Figure 4
Roots in Complex Plane
The two roots in the complex plane are illustrated in Figure 5. It is a circular shape with the roots lying on the boundary of the shape. The values for each root are given.
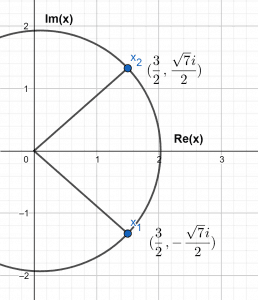
Figure 5
Roots
Now, as the discriminant of the input equation is less than zero, the calculator gives both roots of complex nature (real and imaginary).
disc < 0
The roots are given as:
\[ x_{1} = \frac{3}{2} – \frac{i\sqrt{7}}{2} \]
\[ x_{2} = \frac{3}{2} + \frac{i\sqrt{7}}{2} \]
Example 2
Determine the roots of the following equation:
\[9x^2-12x+4=0\]
Also, draw a root plot in the x-y coordinate system.
Solution
Root Plot
The roots of the equation can be represented on the cartesian coordinate system like Figure 6:
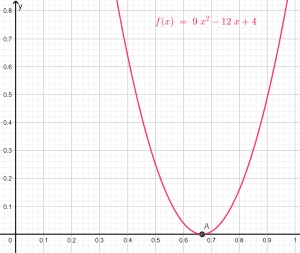
Figure 6
Number Line
The roots can also be shown on the number line. It is shown in figure 7 below:

Figure 7
Roots
When you put the expression in the calculator, you will get real and equal roots since the discriminant is zero.
disc = 0
The roots are given as:
\[x_{1,2}=\frac{2}{3} \]
Example 3
Consider the following equation:
\[ 2x^2 – 11x + 5 = 0 \]
Use the Quadratic Formula Calculator to solve the equation.
Solution
Root Plot
The root plot for the input equation is shown in Figure 8. The graph is an upward parabola with a global minimum below the x-axis. It has also highlighted the location of roots.
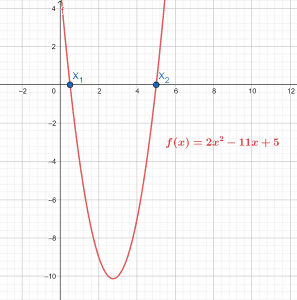
Figure 8
Number Line
The roots are simple values of x, so they are represented in the x plane as a form of the number line. The points in the x plane have only one dimension, which is demonstrated in Figure 9.

Figure 9
Roots
Now as the discriminant of the input equation is greater than zero and a perfect square, the obtained roots are real, different, and rational.
\[ x_{1} = \frac{1}{2} \]
\[ x_{2} = 5 \]
Example 4
Let’s say we have the following quadratic equation.
\[ -x^2 + 4x + 4 \]
Find the values of x that satisfy it.
Solution
Root Plot
The graph in the cartesian coordinate system for the given equation is shown in Figure 10. It is a downward parabola with a global maximum above the x-axis.
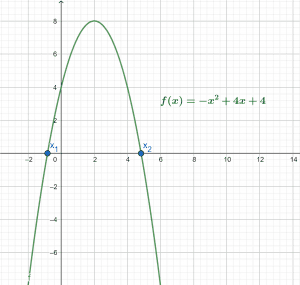
Figure 10
Number Line
As the equation has only one variable x, so the values are represented in the x plane in Figure 11.

Figure 11
Roots
Now if the discriminant is calculated, it turns out to be a positive number but not a perfect square. The calculator gives real, irrational, and distinct values.
The roots of the equation are given as:
\[ x_{1} = 2 – 2\sqrt{2} \]
\[ x_{2} = 2(1 + \sqrt{2}) \]
All the Mathematical Images/Graphs are created using GeoGebra.
