JUMP TO TOPIC
Rational Exponents Calculator + Online Solver With Free Steps
The Rational Exponents Calculator evaluates the exponent of a given input number or expression, provided the exponent is rational.
Exponents, indicated by ‘^’ or superscript as in $x^n$ with n as the exponent, depict the operation of “raising to a power.” In other words, this means multiplying the expression or number by itself n times:
\[ y^n = y \quad \underbrace{\times}_{k\,=\,1} \quad y \quad \underbrace{\times}_{k\,=\,2} \quad \cdots \quad \underbrace{\times}_{k\,=\,n-1} \quad y \quad \underbrace{\times}_{k\,=\,n} \quad y \]
Which shortens to:
\[ y^n = \prod_{k=1}^n y \]
The calculator supports variable and multi-variable inputs for both the expression and the exponent. The result sections change quite a lot depending on both the type and magnitude of the input. Thus, the calculator always presents the results in the most relevant and appropriate form.

What Is the Rational Exponents Calculator?
The Rational Exponents Calculator is an online tool that raises an input number or expression (with or without variables) to the power of a provided rational exponent. The exponent may also be variable.
The calculator interface consists of two text boxes placed next to each other, separated by a ‘^’ indicating the exponentiation. In the first text box to the left of the ^ symbol, you enter the number or expression whose exponent you want to evaluate. In the second box to the right, you enter the value of the exponent itself.
How To Use the Rational Exponents Calculator?
You can use the Rational Exponents Calculator to find the exponent of a number or an expression by entering the number/expression and the value of the exponent into the text boxes.
For example, suppose you want to evaluate $37^4$. You can use the calculator to do so using the step-by-step guidelines below.
Step 1
Enter the number/expression in the first text box to the left. For the example, enter “37” without quotes.
Step 2
Enter the exponent value in the second text box to the right. For the example, you would enter “4” without quotes here.
Step 3
Press the Submit button to get the results.
Results
The result section is expansive and depends heavily on the type and magnitude of the input. Two of these sections, however, are always displayed:
- Input: The input expression as the calculator interprets it in LaTeX format (for manual verification). For our example, 37^4.
- Result: The actual result value. For our example, this is 1874161.
Let a, b be two constant coefficients, and x, y be two variables for the following text.
Constant Value to a Constant Exponent
Our example falls in this category. The results contain (sections marked with * appear always):
- *Number Line: The number as it falls onto the number line (up to an appropriate zoom level).
- Number Name: The pronunciation of the resulting value – is only displayed if the result is in non-scientific notation.
- Number Length: The number of digits in the result – only appears when it exceeds five digits. For our example, this is 7.
- Visual Representation: The resulting value in the form of dots. This section shows only when the result is an integer value strictly smaller than 39.
- Comparison: This section shows if the resulting value compares to some known quantity. For our example, it is almost half of the possible arrangements for a 2x2x2 Rubik’s cube ($\approx$ 3.7×10^6).
Other sections might appear as well for decimal exponents.
Variable Value to a Constant Exponent
For input expressions of the type $f(x) = x^a$ or $f(x,\, y) = (xy)^a$, the following sections appear:
- 2D/3D Plot: Plot of the function over a range of the variable’s values. 2D if only one variable is present, 3D if two, and none if more than two.
- Contour Plot: The contour plot for the resulting expression – only appears if there is a 3D plot for the result.
- Roots: The roots of the expression, if they exist.
- Polynomial Discriminant: The discriminant of the resulting expression. Found using the known equations for low-degree polynomials.
- Properties as a Function: The domain, range, parity (even/odd function), and periodicity (if it exists) for the resulting expression expressed as a function.
- Total/Partial Derivatives: The total derivative of the resulting expression if only one variable is present. Otherwise, for more than one variable, these are partial derivatives.
- Indefinite Integral: The indefinite integral of the resulting function w.r.t one variable. If more than one variable is present, the calculator evaluates the integral w.r.t. the first variable in alphabetical order.
- Global Minima: The minimum value of the function – only appears when roots exist.
- Global Maxima: The maximum value of the function – only shows if roots exist.
- Limit: If the resulting expression represents a converging function, this section shows the convergence value as a limit of the function.
- Series Expansion: The result expanded about a value of the variable using a series (generally Taylor). If more than one variable, the expansion is done w.r.t. the first variable in alphabetical order.
- Series Representation: The result in the form of a series/summation – shown only if possible.
Constant Value to a Variable Exponent
For input expressions of the type $a^x$ or $a^{xy}$, the results contain the same sections as in the previous case.
Variable Value to a Variable Exponent
For input expressions of the type $(ax)^{by}$, the calculator again shows the same sections as in the previous variable cases.
Solved Examples
Example 1
Evaluate the expression $\ln^2(40)$.
Solution
Given that:
\[ \ln^2(40) = (\ln40)^2 \]
ln 40 = 3.68888
\[ \Rightarrow \, \ln^2(40) = (3.68888)^2 = \left( \frac{368888}{100000} \right)^2 = \mathbf{13.60783} \]

Figure 1
Example 2
Plot the function $f(x, y) = (xy)^2$.
Solution
Given that:
\[ (xy)^2 = x^2y^2 \]
The calculator plots the function as below:
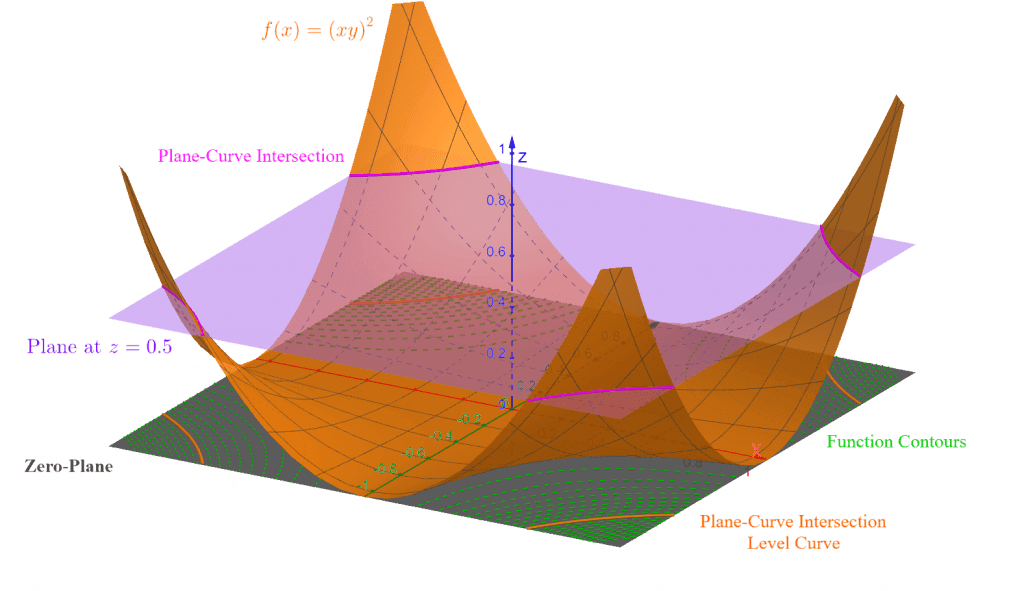
Figure 2
And the contours:
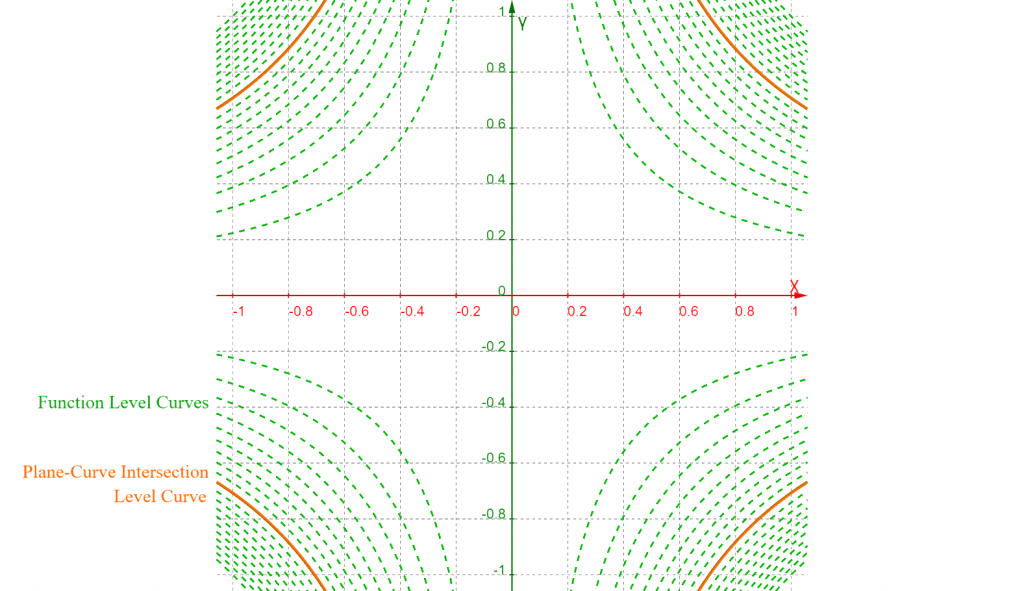
Figure 3
Example 3
Evaluate:
\[ 32^{2.50} \]
Solution
The exponent 2.50 can be expressed as the improper fraction 250/100 and simplified to 5/2.
\[ \therefore \, 32^{2.50} = 32^{ \frac{5}{2} } = \left( 32^\frac{1}{2} \right)^5 \]
\[ 32^{2.50} = \left( \sqrt[2]{32} \right)^5 = \left( \sqrt[2]{2^4 \cdot 2} \right)^5 \]
\[ \Rightarrow 32^{2.50} = (4 \sqrt[2]{2})^5 = (4 \times 1.41421)^5 = \mathbf{5792.545794} \]

Figure 4
All graphs/images were created with GeoGebra.
