JUMP TO TOPIC
Residual Calculator + Online Solver With Free Steps
The Residual Calculator is an advanced online tool that helps to find the residue of any mathematical function. The residue is the coefficient of the first term with negative power in Laurent’s series of functions about a point.
The calculator takes the information regarding the target function and point as the input and returns the residue of the provided function.

What Is the Residual Calculator?
The Residual Calculator is an online calculator that can calculate the residue of any complex function with the speed of knots.
It becomes challenging to deal with these calculations if solved manually. Therefore, we offer you the Residual Calculator that solves your problem by quickly determining the residue.
This tool’s high accuracy and precision make it reliable and efficient. It is a powerful tool for helping mathematicians and students find solutions easily and quickly.
To find the residue, you first need to find Laurent’s series and then extract the coefficient from the resultant expression at the given point. This method involves numerous calculations and approximations.
How To Use the Residual Calculator?
You can use the Residual Calculator by entering your function’s expression and a point in the provided space. You can follow the steps given below to use the calculator correctly.
Step 1
Put the expression of the function for which you want to solve the problem in the ‘Residue of’ box.
Step 2
Insert the target point where you want to calculate the residue in the same field and separate it with a comma. It is actually a pole of the complex function.
Step 3
Press the ‘Submit’ button to get the solution.
Result
The result of the calculator varies on the expression provided at the input. If the pole is defined explicitly in the input, then it gives the resultant residue at the pole.
If the pole is not provided, then the calculator finds the pole and displays the value of the pole and the residue at the pole. Also, it gives the representation of the zeros and poles of the function in a complex plane.
How Does the Residual Calculator Work?
The residual calculator works by finding the residue of a given function. It calculates the residue value at a simple pole and a higher order pole of a process. It also provides the pole-zero plot.
The usage of this calculator will be cleared by knowing the concept behind the residue value and the poles of a function.
What Is Residue?
The residue of a function ‘f’ at a value ‘c’ is the coefficient $b_{-1}$ of the first negative power term in the Laurent series expansion of function ‘f’ at constant ‘c.’
It can be defined mathematically by considering the isolated singular function ‘f(z)’ at $z_{0}$ with the Laurent series expansion of ‘f(z)’ given by:
\[f(z) = \displaystyle\sum_{n=0} ^{\infty} a_n{(z-z_o)^n} + \displaystyle\sum_{n=1} ^{\infty} \frac{b_n}{(z-z_o)^n}\]
In the above expansion, the residue of ‘f(z)’ at $z_{0}$ is the coefficient $b_{1}$ which is represented by $Res_{(z=z_{0})} f$ = $b_{1}$.
The above residue is defined for the function that has isolated singularity at $z_{0}$.
The isolated singular point $z_{0}$ of a function is that point in the complex plane for the function is defined and differentiable at every point except the point $z_{0}$ itself.
How To Find the Residue Value?
The residue value can be found through the Laurent series since the coefficient of the first negative term in the expansion represents its value. However, it is a tedious task.
The simple and standard method to determine the residue is through the formulae that find the residue at the poles of the given function. The calculation of the residues at the poles made the task very easy.
Residue at Simple Pole
The pole of the function with power equal to one is known as a simple pole. The limit formula gives the residue at a simple pole, and it is defined below.
If a function ‘f(z)’ has a simple pole at $z_{0}$ and it has an isolated singularity at $z_{0}$, then the residue at that simple pole is given by:
\[Res_{(z=z_{0})} = b_{1} = \lim_{z\to z_{0}} (z-z_{0}) f(z) \]
In the above formula, if the limit does not exist, there is no isolated singularity at $z_{0}$. If the limit is equal to zero, there is a removable singularity, and if the pole is of a higher order, then the limit results in infinity.
Residue at Higher Order Pole
The formula also gives the residue at higher order poles as at the simple poles.
If a function ‘f(z)’ has a pole of order ‘m’ at $z_{0}$ and the isolated singularity for the function exists at $z_{0}$, then the residue is calculated using the following formula:
\[Res_{(z=z_{0})} = b_{1} = \frac{1}{(m-1)!} \, \lim_{z\to z_{0}} \frac{d^{(m-1)}}{d\,z^{(m-1)}} ((z-z_{0})^m f(z)) \]
This formula is very handy in finding the residue for the poles that have low power; however, for the higher power poles, it becomes very complex. Therefore, in that case, finding the residue through Laurent series expansion becomes easier.
Solved Examples
Let’s solve problems using the Residual Calculator to enhance the concepts and working of the calculator.
Example 1
A feedback-based control system has the following transfer function.
\[ f(z) = \dfrac{z^2 + 2}{z + 3} \]
Find the poles for this function and residue at the resultant bars.
Solution
The calculator gives the following results for the above problem.
Residue
The residue for the transfer function is given below.
\[\underset{z=-3}{\text{Res}} \left(\frac{z^2 + 2}{z + 3} \right) = 11\]
Poles
The given function has only one pole, which is given below.
z = -3 (simple pole)
Pole-Zero Plot
Figure 1 shows the pole and zeros for the given function plotted in a complex plane.
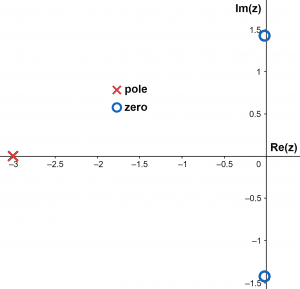
Figure 1
Example 2
Consider the function given function:
\[ f(z) = \frac{\cos{(z)}}{z^4\, – \,1} \]
Find the residue of the function at point z=i.
Solution
Residue
Now the point is defined; therefore, the calculator only returns the value of residue at this point, which is given as follows:
\[ \underset{z=i}{\text{Res}} \left(\frac{\cos{z}}{z^4\, -\, 1} \right) = \frac{1}{4}i\cosh{(1)} \]
