JUMP TO TOPIC
Sequence Convergence Calculator + Online Solver With Free Steps
The Sequence Convergence Calculator is an online tool that determines the convergence or divergence of the function.
The calculator takes a function with the variable n in it as input and finds its limit as it approaches infinity. The result is a definite value if the input function is convergent, and infinity ($\infty$) if it is divergent.
Multivariate functions are also supported, but the limit will only be calculated for the variable $n \to \infty$.

What Is the Sequence Convergence Calculator?
The Sequence Convergence Calculator is an online calculator used to determine whether a function is convergent or divergent by taking the limit of the function as the value of the variable n approaches infinity.
If n is not found in the expression, a plot of the result is returned.
The calculator interface consists of a text box where the function is entered. The input expression must contain the variable n, and it may be a function of other variables such as x and y as well. The input is termed An. The calculator evaluates the expression:
\[\lim_{n \to \infty}A_n\]
The value of convergent functions approach (converges to) a finite, definite value as the value of the variable increases or even decreases to $\infty$ or $-\infty$ respectively.
The convergence is indicated by a reduction in the difference between function values for consecutive values of the variable approaching infinity in any direction (-ve or +ve). That is given as:
\[ f(n=50) > f(n=51) > \cdots \quad \textrm{or} \quad f(n=50) < f(n=51) < \cdots \]
There is no restriction on the magnitude of the difference. That is entirely dependent on the function itself. It is also not possible to determine the convergence of a function by just analyzing an interval, which is why we must take the limit to infinity.
For near convergence values, however, the reduction in function value will generally be very small.
Divergent functions instead grow unbounded as the variable’s value increases, such that if the variable becomes very large, the value of the function is also a very large number and indeterminable (infinity).
A very simple example is an exponential function given as:
\[ f(n) = n^2 \]
How To Use Sequence Convergence Calculator?
You can use the Sequence Convergence Calculator by entering the function you need to calculate the limit to infinity. Ensure that it contains $n$ and that you enclose it in parentheses ().
For a clear explanation, let us walk through the steps to find the results for the following function:
\[ f(n) = n \ln \left ( 1+\frac{5}{n} \right ) \]
Step 1
Ensure the function contains $n$.
Step 2
Enter the function into the text box labeled “An” as inline math text. For our example, you would type:
n(ln(1+(5/n)))
Step 3
Enclose the function within parentheses (). Our input is now:
(n(ln(1+(5/n))))
Step 4
Press the Submit button to get the results.
Result
The results are displayed in a pop-up dialogue box with two sections at most for correct input.
The two sections are :
Limits
The first section named Limit shows the input expression in the mathematical form of a limit along with the resulting value.
Series Expansion at n
The second section is only shown if a power series expansion (Taylor or Laurent) is used by the calculator, and shows a few terms from the series and its type.
The resulting value will be infinity ($\infty$) for divergent functions. For example, for the function $A_n = n^2$, the result would be $\lim_{n \to \infty}(n^2) = \infty$.
Power series expansion is not used if the limit can be directly calculated. Thus for a simple function, $A_n = f(n) = \frac{1}{n}$, the result window will contain only one section, $\lim_{n \to \infty} \left( \frac{1}{n} \right) = 0$.
If a multivariate function is input, such as:
\[ A_n = f(x, n) = \dfrac{1}{1+x^n} \]
The calculator finds:
\[\lim_{n \to \infty}\left(\frac{1}{1+x^n}\right)\]
In the multivariate case, the limit may involve derivatives of variables other than n (say x). They are represented as $x’, x’’, x^{(3)}, …, x^{(k)}$ for $k^{th}$ derivative of x.
If the input function cannot be read by the calculator, an error message is displayed. If n is not included in the input function, the results will simply be a few plots of that function in different ranges.
Solved Examples
For the following given examples, let us find out whether they are convergent or divergent concerning the variable n using the Sequence Convergence Calculator. If they are convergent, let us also find the limit as $n \to \infty$. The function’s plots are drawn to verify the results graphically.
Example 1
Consider the function $f(n) = \dfrac{1}{n}$. Find whether the given function is converging or diverging.
Solution
Use the Sequence Convergence Calculator.
\[\lim_{n \to \infty}\left ( \frac{1}{n} \right ) = \frac{1}{\infty}\]
Knowing that $\dfrac{y}{\infty} \approx 0$ for all $y \neq \infty$, we can see that the above limit evaluates to zero as:
\[\lim_{n \to \infty}\left ( \frac{1}{n} \right ) = 0\]
The function is convergent towards 0.
The graph for the function is shown in Figure 1:
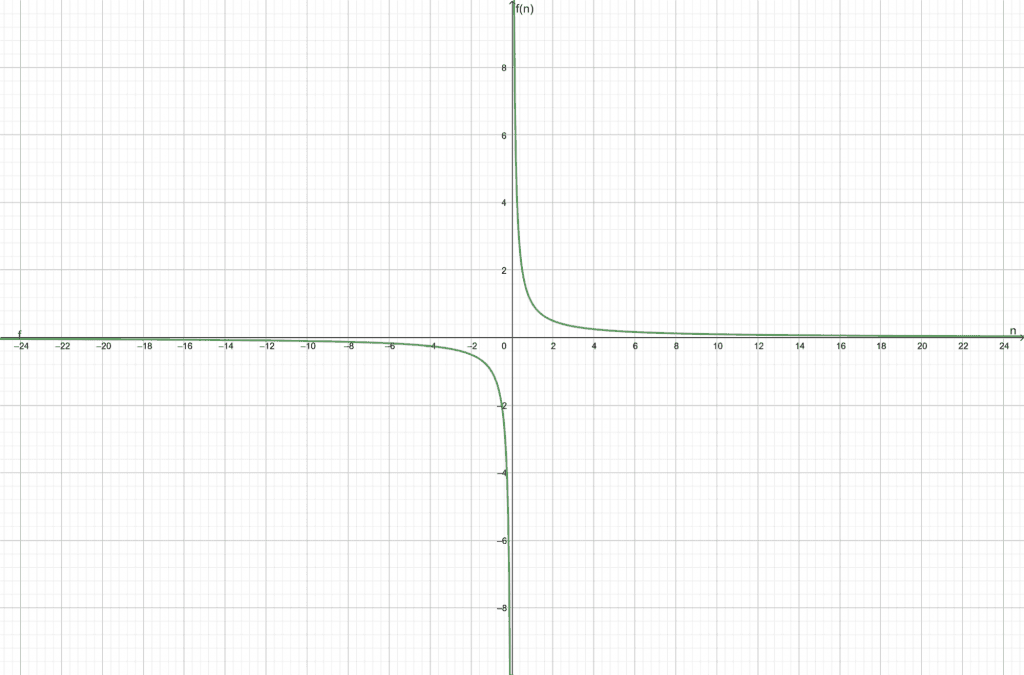
Figure 1
Example 2
The function is given as:
\[f(n) = \dfrac{1}{1-n}\]
Prove that the function is convergent.
Solution:
Using Sequence Convergence Calculator, input the function.
\[\lim_{n \to \infty}\left ( \frac{1}{1-n} \right ) = \frac{1}{1-\infty}\]
Now the calculator will approximate the denominator $1-\infty \approx \infty$ and applying $\dfrac{y}{\infty} \approx 0$ for all $y \neq \infty$, we can see that the above limit evaluates to zero. Thus:
\[\lim_{n \to \infty}\left ( \frac{1}{1-n} \right ) = 0\]
The function is convergent towards 0.
The converging graph for the function is shown in Figure 2:
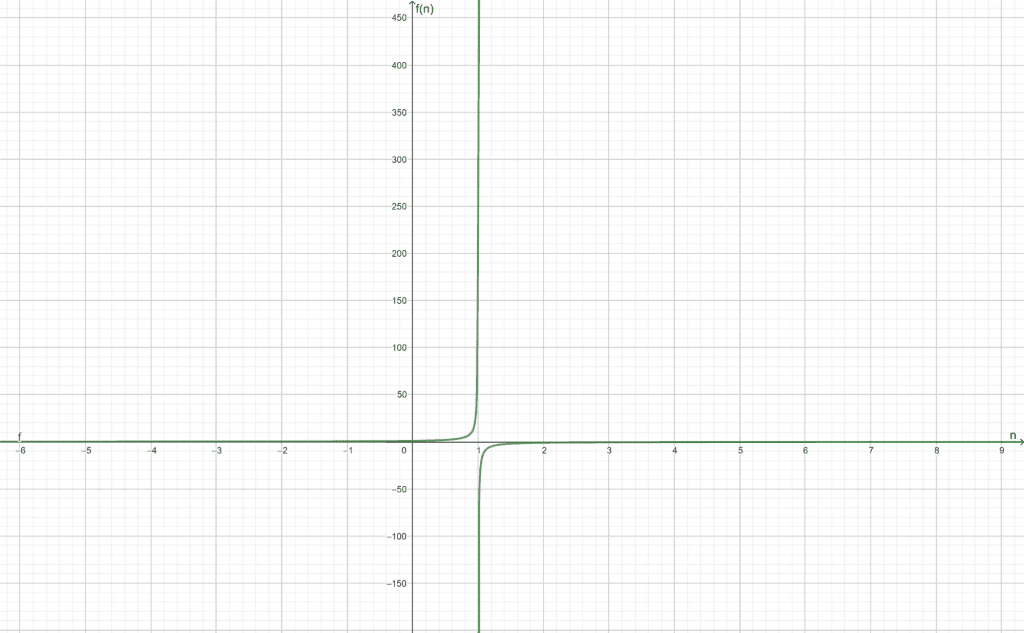
Figure 2
Example 3
Consider the multivariate function $f(x, n) = \dfrac{1}{x^n}$. Find the convergence.
Solution
The function convergence is determined as:
\[ \lim_{n \to \infty}\left ( \frac{1}{x^n} \right ) = \frac{1}{x^\infty} \]
Approximating the denominator $x^\infty \approx \infty$ and applying $\dfrac{y}{\infty} \approx 0$ for all $y \neq \infty$, we can see that the above limit evaluates to zero. Thus,
\[ \lim_{n \to \infty}\left ( \frac{1}{x^n} \right ) = 0\]
The function is convergent towards 0. Because this was a multivariate function in 2 variables, it must be visualized in 3D.
The 3D plot for the given function is shown in Figure 3:
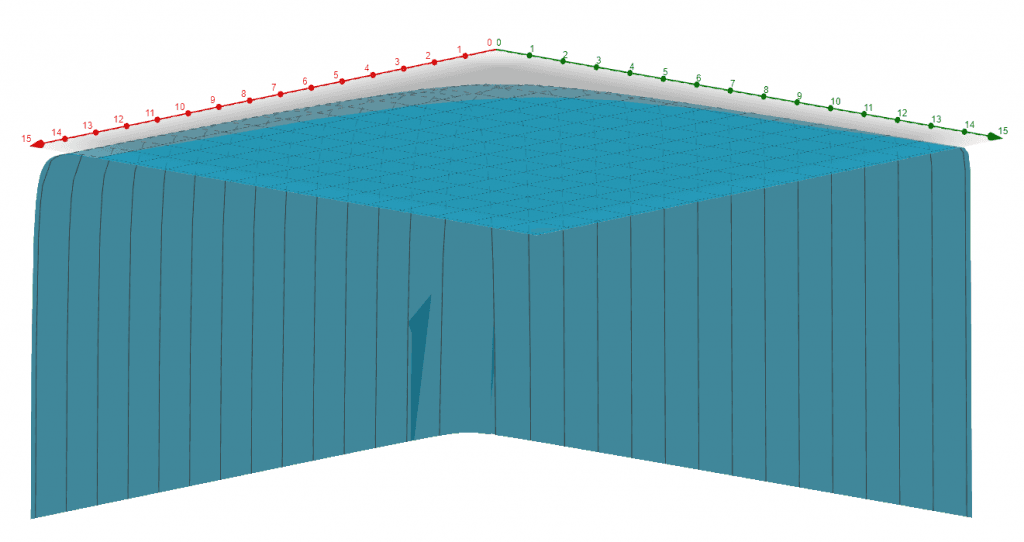
Figure 3
The 3D plot of function is in Example 3, with the x-axis in green corresponding to x, y-axis in red corresponding to n, and z-axis (curve height) corresponding to the value of the function. The curve is planar (z=0) for large values of x and $n$, which indicates that the function is indeed convergent towards 0.
Example 4
Consider the basic function $f(n) = n^2$.
Prove that the function is divergent.
Solution
\[ \lim_{n \to \infty}\left ( n^2 \right ) = \infty^2 \]
Approximating the expression $\infty^2 \approx \infty$, we can see that the function will grow unbounded to some very large value as $n \to \infty$.
So the limit is given as:
\[ \lim_{n \to \infty}\left ( n^2 \right ) = \infty \]
The function is divergent.
The plot of the function is shown in Figure 4:
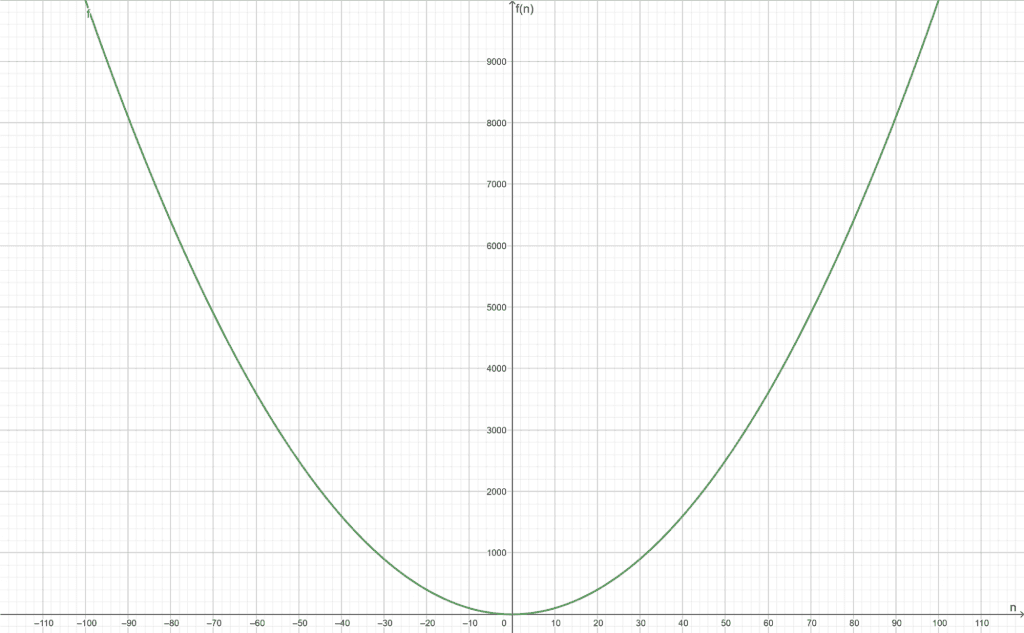
Figure 4
Example 5
Consider the logarithmic function $f(n) = n \ln \left ( 1+\dfrac{5}{n} \right )$.
Find out the convergence of the function.
Solution
This is a relatively trickier problem because f(n) now involves another function in the form of a natural log (ln). We will have to use the Taylor series expansion of the logarithm function.
Please note that the calculator will use the Laurent series for this function due to the negative powers of n, but since the natural log is not defined for non-positive values, the Taylor expansion is mathematically equivalent here.
The general Taylor series expansion around a is defined as:
\[ f(x) = \sum_{k=0}^\infty \frac{f^{(k)}(a)}{k!} (x-a)^k \]
Where a is a real or complex number and $f^{(k)}(a)$ represents the $k^{th}$ derivative of the function f(x) evaluated at point a.
The logarithmic expansion via Maclaurin series (Taylor series with a = 0) is:
\[ \ln(1+x) = x – \frac{x^2}{2} + \frac{x^3}{3} – \frac{x^4}{4} + \cdots \]
Comparing the logarithmic part of our function with the above equation we find that, $x = \dfrac{5}{n}$. Substituting this into the above equation:
\[ \ln \left(1+\frac{5}{n} \right) = \frac{5}{n} – \frac{5^2}{2n^2} + \frac{5^3}{3n^3} – \frac{5^4}{4n^4} + \cdots \]
Evaluating powers gives:
\[ \ln \left(1+\frac{5}{n} \right) = \frac{5}{n} – \frac{25}{2n^2} + \frac{125}{3n^3} – \frac{625}{4n^4} + \cdots \]
Substituting this value into our function gives:
\[ f(n) = n \left( \frac{5}{n} – \frac{25}{2n^2} + \frac{125}{3n^3} – \frac{625}{4n^4} + \cdots \right) \]
\[ f(n) = 5 – \frac{25}{2n} + \frac{125}{3n^2} – \frac{625}{4n3} + \cdots \]
Now if we apply the limit $n \to \infty$ to the function, we get:
\[ \lim_{n \to \infty} \left \{ 5 – \frac{25}{2n} + \frac{125}{3n^2} – \frac{625}{4n^3} + \cdots \ \right \} = 5 – \frac{25}{2\infty} + \frac{125}{3\infty^2} – \frac{625}{4\infty^3} + \cdots \]
Setting all terms divided by $\infty$ to 0, we are left with the result:
\[ \lim_{n \to \infty} \left \{ 5 – \frac{25}{2n} + \frac{125}{3n^2} – \frac{625}{4n^3} + \cdots \ \right \} = 5 \]
The function is thus convergent towards 5.
The plot of the logarithmic function is shown in Figure 5:
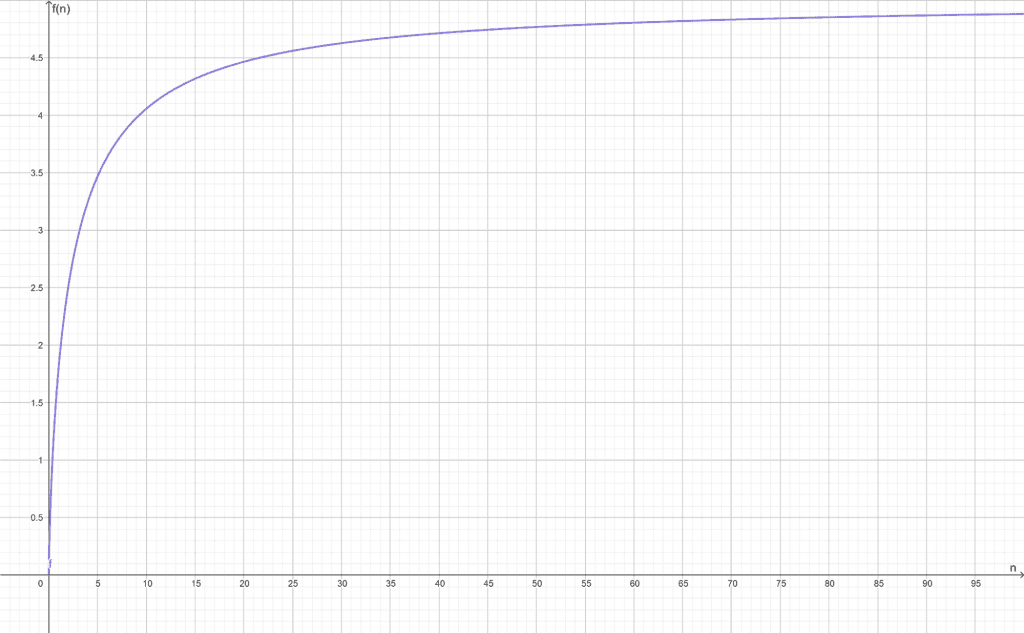
Figure 5
All the Mathematical Images/ Graphs are created using GeoGebra.
