JUMP TO TOPIC
Stoichiometry Calculator + Online Solver With Free Steps
The Stoichiometry Calculator is used to balance the chemical equations on both sides. It takes the chemical equation as input and outputs a balanced equation with the equilibrium constant and many other properties of the reactants and products.
Stoichiometry is an important branch of chemistry that deals with the relationship between quantities. It deals with obtaining equilibrium in a chemical reaction to stabilize the reaction. The reactants chemically react together to give products. The chemical reaction also contains some by-products.
Stoichiometry defines the relationship between the reactants and products by balancing their components.

What Is a Stoichiometry Calculator?
Stoichiometry Calculator is an online tool that balances a chemical reaction by equalizing the components of reactants and products resulting in a balanced equation.
It also provides the chemical structures of reactants and products.
The calculator also outputs the equilibrium constant Kc obtained from the balanced equation. It also gives the rate of reaction and the chemical names for the input reactants and products.
In the end, the calculator also provides the user with a wide range of chemical properties of the input reactants and products.
How To Use Stoichiometry Calculator
You can use the Stoichiometry Calculator by following the steps mentioned here.
Step 1
At first, enter the first reactant of the chemical equation in the Reactant 1 window. The user can enter either the name or the chemical formula for the reactant in this tab.
The first reactant set by default by the calculator is $H_{3} P O_{4}$ which is the chemical formula for phosphoric acid.
Step 2
Enter the second reactant in the Reactant 2 window of the calculator. The calculator can only input chemical equations with two reactants for the stoichiometric calculations.
The name of the reactant or the chemical formula for it can be entered in this window. The calculator sets the second reactant by default as Na OH which is sodium hydroxide.
Step 3
The chemical reaction takes place between the reactants and outputs the products. The products are completely different from the reactants as their chemical properties have now been changed.
Enter the first product obtained from the chemical reaction in the Product 1 window. It could be the name of the product or the chemical formula for it.
Both phosphoric acid $H_{3} P O_{4}$ and sodium hydroxide Na OH react to give water $H_{2} O$ which is set by default in the product 1 window by the calculator. Water $H_{2} O$ is the by-product of this reaction.
The by-products are products of a chemical reaction that are not usually desired at the end of the chemical reaction.
Step 4
Enter the second product of the chemical equation in the window below the title, Product $2$. This calculator takes in the chemical equations with two reactants and two products.
The chemical reaction between $ H_{3} P O_{4} $ and Na OH gives the product $Na_{3} P O_{4} $. This is the chemical formula for trisodium phosphate which is set by default in the Product 2 window.
Step 5
Press the Submit button of the Stoichiometry Calculator for it to process the entered chemical equation having the two reactants and two products.
Output
The calculator processes the input reactants and products and displays the output in multiple windows as follows:
Input Interpretation
The calculator processes the input reactants and products and displays the resulting chemical equation in this window. The reactants and products set by default by the calculator give the following chemical equation:
\[ H_{3} P O_{4} \ + \ Na OH \ \longrightarrow \ H_{2} O \ + \ Na_{3} P O_{4} \]
The user will find the input interpretation according to his/her entered reactants and products.
If any reactant or product is not entered, the calculator prompts Not a valid input, please try again.
Balanced Equation
The balanced equation is obtained by a series of steps performed on the entered chemical equation. A balanced equation is defined as an equation with an equal number of atoms in substances on both sides of the equation.
The balanced equation obtained from the chemical equation set by default by the calculator is:
\[ H_{3} P O_{4} \ + \ 3 Na OH \ \longrightarrow \ 3 H_{2} O \ + \ Na_{3} P O_{4} \]
Note that to balance the equation, the user needs three moles of Na OH to react with one mole of $H_{3} P O_{4}$. So, it produces three moles of $H_{2} O$ and one mole of $ Na_{3} P O_{4} $.
This window also shows the option of Show equation details. By pressing on it, the user can view all the steps to balance the input chemical equation.
Structures
The calculator displays the chemical structures of all the reactants and products in this window. The structures show the chemical bonds between the atoms of all the compounds in the chemical equation.
Word Equation
This output window shows the word equation for the entered reactants and products. It displays the names of the reactants and products in the form of an equation.
The reactants and products, set by default by the calculator, show the following word equation:
Phosphoric acid + Sodium hydroxide $\longrightarrow$ Water + Trisodium Phosphate
Equilibrium Constant
The equilibrium constant is obtained from the balanced chemical equation. The formula for the equilibrium constant Kc is:
\[ K_c = \frac{ {[Product 1]}^{M_{P_{1}}} \ {[Product 2]}^{M_{P_{2}}} }{ {[Reactant 1]}^{M_{R_{1}}} \ {[Reactant 2]}^{M_{R_{2}}} } \]
Where,
$M_{P_{1}}$ is the number of moles of the first product P1 produced in the balanced chemical reaction.
$M_{P_{2}}$ is the number of moles of the second product P2 in the balanced equation.
$M_{R_{1}}$ is the number of moles of the first reactant R1 balanced in the input equation.
$M_{R_{2}}$ is the number of moles of the second reactant R2 balanced in the equation.
The reactants and products, set by default by the calculator, gives the balanced equation as:
\[ H_{3} P O_{4} + 3 Na OH \longrightarrow 3 H_{2} O + Na_{3} P O_{4} \]
The equilibrium constant Kc is obtained from the balanced equation as:
\[ K_c = \frac{ {[ H_{2} O ]}^{3} \ [ Na_{3} P O_{4} ] }{ [ H_{3} P O_{4} ] \ { [Na OH ] }^{3} } \]
Rate of Reaction
The reaction rate is the rate at which the reaction takes place. It is defined as how slow or fast the reactants react to turn into products. The rate of reaction is also obtained from the balanced equation.
The rate of change of reactants and products gives the rate of the reaction. All the reactants and products are divided by $\Delta t$.
The number of moles in the balanced equation is also divided in the rate equation. It is because the greater the number of moles of the reactants or products, the more time it will take for the reaction to take place.
Hence, decreasing the reaction rate. So, the number of moles of the reactants or products is inversely proportional to the rate of reaction.
The rate of reaction for the default set of reactants and products by the calculator is:
\[ Rate = – \frac{ \Delta [ H_{3} P O_{4} ] }{ \Delta t} = – \frac{1}{3} \frac{ \Delta [Na OH] }{ \Delta t} = \frac{1}{3} \frac{ \Delta [H_{2} O] }{ \Delta t} = \frac{ \Delta [Na_{3} P O_{4}] }{ \Delta t} \]
The calculator obtains this equation by assuming the volume constant.
Chemical Names and Formulas
The calculator displays the formula, Hill’s formula and the names of the entered reactants and products in this window.
For the default example, it displays the Hill’s formula for phosphoric acid $H_{3} P O_{4}$ as $H_{3} O_{4} P$.
For sodium hydroxide Na OH, it displays Hill’s formula to be H Na O. For water, $H_{2} O$, Hill’s formula is the same, and for trisodium phosphate $Na_{3} P O_{4}$, Hill’s formula is $Na_{3} O_{4} P$.
For various reactants and products entered by the user, the calculator gives the results accordingly.
Substance Properties
The calculator also outputs some of the chemical properties of the substances entered in the input window. These properties are as follows:
Molar Mass
To understand molar mass, one needs to understand the concept of the mole. One mole of a substance contains 6.022 × $10^{23}$ particles.
The molar mass of a substance is the mass of one mole of that substance.
The calculator displays the molar mass of each reactant and product in this window. The molar mass for the default reactants phosphoric acid and sodium hydroxide is 97.994 g/mol and 39.997 g/mol respectively.
The molar mass for the default products water and trisodium phosphate is 18.015 g/mol and 163.94 g/mol respectively.
Phase
The calculator also displays the phase or state of the reactants and products at STP. STP stands for standard temperature and pressure.
At STP, both the phase of phosphoric acid and water is liquid. The phase of sodium hydroxide and trisodium phosphate is solid at STP.
Melting Point
The melting point of a substance is defined as the temperature at which a solid turns into liquid. The calculator displays the melting points of the reactants and products.
The melting point for the default reactants, $H_{3} P O_{4}$ and Na OH are 42.4 °C and 323 °C respectively. Similarly, for $H_{2} O$ and $Na_{3} P O_{4}$, the melting points are 0 °C and 75 °C respectively.
Boiling Point
The temperature at which a liquid turns into gas is known as the boiling point of the substance. The calculator also displays the boiling points of the input reactants and products.
So, the boiling points for $H_{3} P O_{4}$, Na OH and $H_{2} O$ are 158 °C, 1390 °C and 99.61 °C respectively.
Density
The density of a substance is defined as the mass per unit volume of a substance. The formula for density is:
\[ Density = \frac{m}{V} \]
Where $m$ is the mass and V is the volume of the substance. The calculator also displays the density of every material.
The densities of $H_{3} P O_{4}$, Na OH, $H_{2} O$ and $Na_{3} P O_{4}$ are $1.685 \ g/cm^{3} $, $2.13 \ g/cm^{3} $, $0.997048 \ g/cm^{3} $ and $2.536 \ g/cm^{3} $ respectively.
Solubility in Water
Solubility in water is defined as how much a substance dissolves in water.
In the default example, the calculator shows Na OH and $Na_{3} P O_{4}$ to be soluble and $H_{3} P O_{4}$ to be very soluble in water.
Surface Tension
The surface tension is defined as the force of material on the surface of a liquid. The calculator also displays the surface tension of the reactants and products.
The surface tension of sodium hydroxide and water is 0.07435 N/m and 0.07435 N/m respectively.
Dynamic Viscosity
The calculator also displays the dynamic viscosity of a fluid. The dynamic viscosity measures the force required by the fluid to overcome friction.
The dynamic viscosity of sodium hydroxide is 0.004 Pa.s at 350 °C and that of water is $8.9 × 10^{-4} \ Pa.s$ at 25 °C.
Odor
The odor of a substance is the smell coming from the substance.
In the default chemical equation by the calculator, phosphoric acid, water, and trisodium phosphate are all odorless substances.
Entropy and Enthalpy
The calculator also displays the calculations for entropy and enthalpy for some molecules in the chemical reaction. These are the thermodynamic properties of the particular molecules.
Solved Examples
Following are some solved examples through the Stoichiometry Calculator.
Example 1
Aluminum reacts with hydrochloric acid to give aluminum chloride and hydrogen gas. For how many moles of $Al$ and HCl, the reaction produces the above products $Al Cl_{3}$ and $H_{2}$ in a balanced equation.
Solution
The user enters the equation in the calculator’s input window as follows:
\[ Al \ + \ HCl \ \longrightarrow \ Al Cl_{3} \ + \ H_{2} \]
The calculator shows the above equation in the input interpretation.
In the next window, it shows the above equation in balanced form as follows:
\[ 2 Al \ + \ 6 HCl \ \longrightarrow \ 2 Al Cl_{3} \ + \ 3 H_{2} \]
The calculator also shows the structures of the substances in the chemical equation.
Structure of Al is given as:
\[\mathit{ Al} \]
Structure of HCl is given as:
\[ \mathit{Cl-H} \]
The structure of $AlCl_3$ is given in figure 1 as follows:
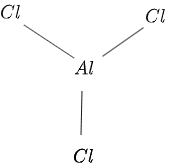
Figure 1
Structure of $H_2$ is given as:
\[ \mathit{H – H } \]
The calculator gives the word equation for the input interpretation equation as follows:
Aluminum + Hydrogen Chloride $\longrightarrow$ Aluminum Chloride + Hydrogen
The calculator also displays the reaction thermodynamics for this equation.
The enthalpy of the above chemical reaction is given as follows:
\[ \Delta {H_{rxn}}^{0} \ = \ -1408 \ kJ/mol \ – \ ( – \ 553.8 \ kJ/mol ) \ = \ – \ 854.6 \ kJ/mol \]
The negative sign of enthalpy indicates an exothermic reaction.
The entropy of the chemical reaction is calculated as follows:
\[ \Delta {S_{rxn}}^{0} \ = \ 567 \ J/(mol.K) \ – \ ( 1179 \ J/(mol.K) ) \ = \ – \ 611.6 \ J/(mol.K) \]
The negative sign of entropy of the chemical reaction indicates an exo-entropic reaction.
The equilibrium constant for the balanced equation is given as follows:
\[ K_c = \frac{ {[ Al Cl_{3} ]}^{2} \ {[ H_{2}]}^{3} }{ {[ Al ]}^{2} \ { [HCl] }^{6} } \]
The rate of reaction given by the calculator is,
\[ Rate = – \frac{1}{2} \frac{ \Delta [ Al ] }{ \Delta t} = – \frac{1}{6} \frac{ \Delta [HCl] }{ \Delta t} = \frac{1}{2} \frac{ \Delta [Al Cl_{3}] }{ \Delta t} = \frac{1}{3} \frac{ \Delta [H_{2}] }{ \Delta t} \]
The calculator also provides the chemical names and formulas for the reactants and products.
The IUPAC name for $Al Cl_{3}$ is trichloroalumane. The calculator also shows Hill’s formula for the reactants and products.
The calculator also provides the chemical properties of the reactants and products as shown in table 1.
Al | HCl | $Al Cl_{3}$ | $H_{2}$ | |
Molar Mass (g/mol) | 26.9815 | 36.46 | 133.3 | 2.016 |
Phase (at STP) | solid | gas | solid | gas |
Melting Point(°C) | 660.4 | -114.17 | 190 | -259.2 |
Boiling Point(°C) | 2460 | -85 | -252.8 | |
Density ($g/cm^{3}$) | 2.7 | 0.00149 | $8.99 × 10^{-5}$ | |
Solubility in Water | insoluble | miscible | ||
Surface Tension (N/m) | 0.817 | |||
Dynamic Viscosity (Pa.s) | $1.5 × 10^{-4}$ | $8.9 × 10^{-4}$ | ||
Odor | odorless | odorless |
Table 1
Example 2
Ammonia reacts with oxygen gas to produce water and nitric oxide. How many moles of ammonia $NH_{3}$ and oxygen $O_{2}$ are required to produce a balanced equation with water $H_{2} O$ and nitric oxide NO?
Solution
The calculator takes the input reactants and products and outputs the input interpretation of the chemical equation as follows:
\[ N H_{3} \ + \ O_{2} \ \longrightarrow \ H_{2} O \ + \ NO \]
The calculator balances the equation and shows the balanced equation as follows:
\[ 4 N H_{3} \ + \ 5 O_{2} \ \longrightarrow \ 6 H_{2} O \ + \ 4 NO \]
In the structures window, the calculator displays the structures of the reactants and products showing bonds between the atoms.
The structure of $ N H_{3} $ is shown in figure 2 as follows:
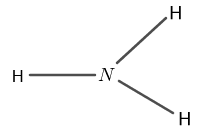
Figure 2
The structure of $O_{2}$ is given as follows:
\[ \mathit{O=O} \]
The structure for $H_{2} O$ is given in figure 3 as follows:
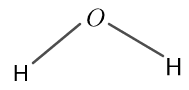
Figure 3
The structure of NO is given as follows:
\[ \mathit{N=O} \]
The calculator also provides the word equation for the chemical equation as follows:
Ammonia + Oxygen $\longrightarrow$ Water + Nitric Oxide
The Reaction thermodynamics for this equation is also displayed by the calculator.
The enthalpy of the chemical reaction is given as follows:
\[ \Delta {H_{rxn}}^{0} \ = \ -1350 \ kJ/mol \ – \ ( – \ 183.6 \ kJ/mol ) \ = \ – \ 1166 \ kJ/mol \]
The reaction is exothermic as enthalpy is negative.
The Gibbs free energy is also calculated by the calculator as follows:
\[ \Delta {G_{rxn}}^{0} \ = \ – \ 1072 \ kJ/mol \ – \ ( – \ 65.6 \ kJ/mol ) \ = \ – \ 1007 \ kJ/mol \]
The value of Gibbs free energy indicates an exergonic reaction.
The entropy of the chemical reaction is calculated as follows:
\[ \Delta {S_{rxn}}^{0} \ = \ 1263 \ J/(mol.K) \ – \ ( 1797 \ J/(mol.K) ) \ = \ – \ 533.5 \ J/(mol.K) \]
The negative sign of entropy indicates an exo-entropic chemical reaction.
The calculator gives the equilibrium constant for the balanced equation as follows:
\[ K_c = \frac{ {[ H_{2} O]}^{6} \ {[ NO ]}^{4} }{ {[ N H_{3} ]}^{4} \ { [ O_{2} ] }^{5} } \]
The rate of reaction for this equation is given by the calculator as follows:
\[ Rate = – \frac{1}{4} \frac{ \Delta [ N H_{3} ] }{ \Delta t} = – \frac{1}{5} \frac{ \Delta [ O_{2} ] }{ \Delta t} = \frac{1}{6} \frac{ \Delta [ H_{2} O ] }{ \Delta t} = \frac{1}{4} \frac{ \Delta [ NO ] }{ \Delta t} \]
The calculator also provides the chemical names and formulas for the reactants and products. Hill’s formula for ammonia is $H_{3} N$.
The calculator also displays the substance properties of the reactants and products as shown in table $2$.
$NH_{3}$ | $O_{2}$ | $H_{2} O$ | NO | |
Molar Mass (g/mol) | 17.031 | 31.998 | 18.015 | 30.006 |
Phase (at STP) | gas | gas | liquid | gas |
Melting Point (°C) | -77.73 | -218 | 0 | 163.6 |
Boiling Point (°C) | -33.33 | -183 | 99.61 | – 151.7 |
Density ($g/cm^{3}$) | $6.96 × 10^{-4}$ | 0.001429 | 0.997048 | 0.001226 |
Surface Tension (N/m) | 0.0234 | 0.01347 | 0.0728 | |
Dynamic Viscosity (Pa.s) | $1.009 × 10^{-5}$ | $2.005 × 10^{-5}$ | $8.9 × 10^{-4}$ | $1.911 × 10^{-5}$ |
Odor | odorless | odorless |
Table $2$
Therefore, the Stoichiometry Calculator is a powerful tool for determining the chemical properties of a substance.
All images are created using GeoGebra.
