• Home
  • >
  • Partial Derivatives – Definition, Properties, and Example

Partial Derivatives – Definition, Properties, and Example

Knowing how to calculate partial derivatives allows one to study and understand the behavior of multivariable functions.   This opens a wide range of applications in Calculus such as the tangent planes, Lagrange multipliers, and more. For now, it’s important that we have a strong understanding of partial differentiation.The partial derivatives allow us to understand how a multivariable function changes with respect to a specific variable.  Partial differentiation works by treating the rest of the variables as constant.In this article, we’ll cover the fundamentals of partial derivatives. This includes the partial derivative’s formal definition, common notations, and the techniques we can apply to calculate first-order, second-order, and even higher-order partial derivatives of different functions!

What Is a Partial Derivative?

The partial derivative of a function represents the derivative of the function with respect to one of the function’s variables. There are instances when functions are defined by more than one independent variable. For multivariable functions, their values will change when one or more of the input values change.\begin{aligned}f(x, y) &= x^2y + 2xy – y^2\\g(x, y) &= \sin xy – \cos xy\\h(x, y, z) &= x^2 – 2xyz + yz + z^2\end{aligned}For us to calculate the rate of change of these functions with respect to one variable, we’ll have to hold the remaining variables constant. 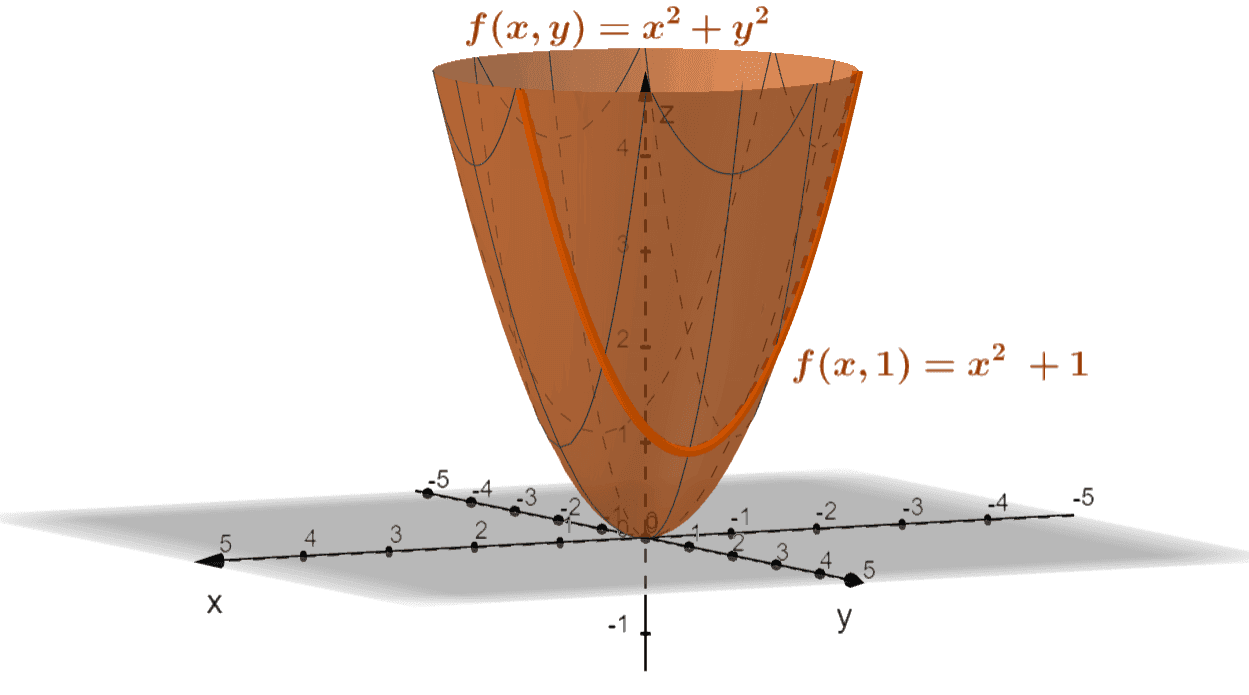We call this process partial differentiation and the rate of change to be the partial derivative of the function with respect to the variable we’re studying.graph of multivariable functionsHere’s an example of the curve formed by a function with two variables: $f(x, y)  = x^2 + y^2$. If we set $y$ to be equal to $1$, we’ll be focusing on the plane that contains all values of $f(x, y)$ where $y =1$. When this happens, we’re working with $f(x, 1) = x^2  +1$,  and it’ll be easier for us to measure the rate of change of $f(x, y)$ with respect to $x$.We’ll be using a similar process to calculate the partial derivatives of multivariable functions. To establish the partial derivative’s formal definition, we need to better understand how variables affect multivariable functions such as $f(x,y) = x^2y + 2xy – y^2$. So, why don’t we construct a table of values highlighting key values of $x$ and $y$?
\begin{aligned}\boldsymbol{x} \backslash^{\displaystyle\boldsymbol{y}}\end{aligned}\begin{aligned}-2 \end{aligned}\begin{aligned}-1 \end{aligned}\begin{aligned}0 \end{aligned}\begin{aligned}1 \end{aligned}\begin{aligned}2 \end{aligned}
\begin{aligned}-2 \end{aligned}\begin{aligned}-4 \end{aligned}\begin{aligned}\color{Teal}-1 \end{aligned}\begin{aligned}0 \end{aligned}\begin{aligned}1 \end{aligned}\begin{aligned}4 \end{aligned}
\begin{aligned}-1 \end{aligned}\begin{aligned}-2 \end{aligned}\begin{aligned}\color{Teal} 0\end{aligned}\begin{aligned}0 \end{aligned}\begin{aligned}-2\end{aligned}\begin{aligned}-6\end{aligned}
\begin{aligned}0 \end{aligned}\begin{aligned}-4 \end{aligned}\begin{aligned}\color{Teal} -1 \end{aligned}\begin{aligned}0 \end{aligned}\begin{aligned}-1 \end{aligned}\begin{aligned}-4 \end{aligned}
\begin{aligned}\color{Teal}1 \end{aligned}\begin{aligned}\color{Teal}-10 \end{aligned}\begin{aligned}\color{Teal}-4 \end{aligned}\begin{aligned}\color{Teal}0 \end{aligned}\begin{aligned}\color{Teal}2 \end{aligned}\begin{aligned}\color{Teal}2 \end{aligned}
\begin{aligned}2 \end{aligned}\begin{aligned}-20 \end{aligned}\begin{aligned}\color{Teal}-9 \end{aligned}\begin{aligned}0 \end{aligned}\begin{aligned}7 \end{aligned}\begin{aligned}12\end{aligned}
We’ve highlighted one column and one row to focus our understanding on what happens when we set either $x$ or $y$ as a constant variable. Let’s say we want to observe a focus on the behavior of $f(x, y)$ when $y = -1$. We can estimate $f\prime(x)$ when $x = 1$ by the formal definition of rates of change as shown below.\begin{aligned}f\prime(1) &= \lim_{h \rightarrow 0} \dfrac{f(1 + h) – f(1)}{h}\\&= \lim_{h \rightarrow 0} \dfrac{f(1 + h, -1) – f(1, -1)}{h}\end{aligned}We can approximate the rate of change with respect to $x$ by using $h = 1$ and $h = -1$.
\begin{aligned}\boldsymbol{h = -1}\end{aligned}\begin{aligned}\boldsymbol{h = 1}\end{aligned}
\begin{aligned}f\prime(1) &=\dfrac{f(1 + -1) – f(1)}{-1}\\&= \dfrac{f(1 + -1, -1) – f(1, -1)}{-1}\\ &=\dfrac{f(0, -1) – f(1, -1)}{-1}\\&= \dfrac{1 – -4}{-1}\\&= -5\end{aligned}\begin{aligned}f\prime(1) &=\dfrac{f(1 + 1) – f(1)}{1}\\&= \dfrac{f(1 + 1, -1) – f(1, -1)}{1}\\&=\dfrac{f(2, -1) – f(1, -1)}{1}\\&= \dfrac{-9 – -4}{1}\\&= -5\end{aligned}
From this, we can see that the derivative of $f\prime(1)$ is approximately equal to $-5$.  What does this mean? When $x = 1$ and $y = -1$, the average value of $f(x, y)$ decreases by $5$ for every value of $x$ and $y$ increases.Now, let’s expand our understanding of partial derivatives by formally defining them in terms of limits then eventually set up a simpler process to represent partial derivatives.

Partial Derivative Definition

To understand the underlying principles behind partial derivatives, let’s first understand the formal definition of partial derivatives through limits. Let’s say we have a continuous function, $z = f(x, y)$, we can define the following:i. The partial derivative of $\boldsymbol{f(x, y)}$ with respect to $\boldsymbol{x}$ can be defined as:\begin{aligned}f_x(x, y) &= \lim_{h \rightarrow 0} \dfrac{f(x + h, y) – f(x, y)}{h}\end{aligned}ii. The partial derivative of $\boldsymbol{f(x, y)}$ with respect to $\boldsymbol{y}$ can be defined as:\begin{aligned}f_y(x, y) &= \lim_{h \rightarrow 0} \dfrac{f(x , y + h) – f(x, y)}{h}\end{aligned}For example, we can show that when $f(x, y) = x^2 + y^2$, $f_x(x, y) = 2x$ by using the limit-based definition of $f(x, y)$ as shown below.\begin{aligned}f_x(x, y) &= \lim_{h \rightarrow 0} \dfrac{f(x + h, y) – f(x, y)}{h}\\&= \lim_{h \rightarrow 0} \dfrac{(x + h)^2 + y^2 – (x^2 + y^2)}{h}\\&= \lim_{h \rightarrow 0} \dfrac{x^2 + 2xh + h^2 +y^2 – x^2 – y^2}{h}\\ &= \lim_{h \rightarrow 0} \dfrac{2xh + h^2}{h}\\& = \lim_{h \rightarrow 0} \dfrac{h(2x + h)}{h}\\&= \lim_{h \rightarrow 0} (2x + h)\\&= 2x\end{aligned}This confirms that the partial derivative of $f(x, y)$ with respect to $x$ is equal to $2x$. As with our derivative lessons in the past, calculating the derivative of a function is tedious if we use the limit-based definition. This is why it’s important that we establish easier notations and processes for partial differentiation.

Partial Derivative Notation

There are different notations we can use to represent partial derivatives. One of the most common notations is $\dfrac{\partial f}{\partial x}$ or $\dfrac{\partial f}{\partial y}$. We call the symbol $\partial$, “del”, and this is one of the surest ways to know that we’re evaluating the partial derivative of the function.Let’s say we have $f(x, y) = 2x^2 – 4xy + y^2$, we can represent the partial derivatives:
  • with respect to $x$ as $\dfrac{\partial f}{\partial x}$
  • with respect to $y$ as $\dfrac{\partial f}{\partial y}$
\begin{aligned}\boldsymbol{\dfrac{\partial f}{\partial x}}\end{aligned}\begin{aligned}\boldsymbol{\dfrac{\partial f}{\partial y}}\end{aligned}
\begin{aligned}\dfrac{\partial f}{\color{Teal}\partial x} &=\underbrace{\dfrac{\partial }{\color{Teal}\partial x} (2{\color{Teal}x^2} – 4{\color{Teal}x}y + y^2)}_{\displaystyle{\text{Take the derivative of }x}}\\&\phantom{xxx}\text{Treat} y \text{ as a constant}\\&= 2({\color{Teal}2x}) – 4({\color{Teal}1})y + 0\\&= 4x – 4y \end{aligned}\begin{aligned}\dfrac{\partial f}{\color{DarkOrange}\partial y} &=\underbrace{\dfrac{\partial }{\color{DarkOrange}\partial y} (2{x^2} – 4x{\color{DarkOrange}y} + {\color{DarkOrange}y^2})}_{\displaystyle{\text{Take the derivative of }y}}\\&\phantom{xxx}\text{Treat} x \text{ as a constant}\\&= 0- 4x({\color{DarkOrange}1}) + {\color{DarkOrange}2y}\\&= -4x + 2y\\&= 2y – 4x \end{aligned}
 There are other ways for us to represent partial derivatives such as $f_x$ or $f_1$. For $f_1$, the number represents the order of the variable, so for this case, we want to take the partial derivative of $f$ with respect to the first variable.
Suppose that $z = f(x, y)$ is a continuous function, we can write their partial derivatives using any of the following notations:\begin{aligned}f_x(x, y) = f_x = \dfrac{\partial}{\partial x}f(x, y) = \dfrac{\partial z}{\partial x} = f_1 = D_1f = D_xf\\f_y(x, y) = f_y = \dfrac{\partial}{\partial y}f(x, y) = \dfrac{\partial z}{\partial y} = f_2 = D_2f = D_yf\end{aligned}
Here are some common phrases you’ll hear when working with $\dfrac{\partial f}{\partial x}$:
  • “Del $f$ over del $x$.”
  • “Partial of $f$ with respect to $x$.”
  • “The partial derivative of $f$ with respect to $x$.”
  • “Partial derivative of $f$ with respect to the first variable.”
In the past, we’ve learned about second derivatives and higher order derivatives. The concept can be extended to partial derivatives, but this time, we can have mixed partial derivatives such as $f_{xy}$ or $f_{yx}$. Let us summarize the notations for second partial derivatives:i. The second partial derivative of $\boldsymbol{f(x, y)}$ with respect to $\boldsymbol{x}$ then $\boldsymbol{x}$ can be represented as:\begin{aligned}\dfrac{\partial}{\partial x}\left( \dfrac{\partial f}{\partial x}\right ) = \dfrac{\partial^2 f}{\partial x^2} = f_{xx}\end{aligned}ii. The second partial derivative of $\boldsymbol{f(x, y)}$ with respect to $\boldsymbol{y}$ then $\boldsymbol{y}$ can be represented as:\begin{aligned}\dfrac{\partial}{\partial y}\left( \dfrac{\partial f}{\partial y}\right ) = \dfrac{\partial^2 f}{\partial y^2} = f_{yy}\end{aligned}iii. The second partial derivative of $\boldsymbol{f(x, y)}$ with respect to $\boldsymbol{x}$ then $\boldsymbol{y}$ can be represented as:\begin{aligned}\dfrac{\partial}{\partial y}\left( \dfrac{\partial f}{\partial x}\right ) = \dfrac{\partial^2 f}{\partial y \partial x} = f_{xy}\end{aligned}iv. The second partial derivative of $\boldsymbol{f(x, y)}$ with respect to $\boldsymbol{y}$ then $\boldsymbol{x}$ can be represented as:\begin{aligned}\dfrac{\partial}{\partial x}\left( \dfrac{\partial f}{\partial y}\right ) = \dfrac{\partial^2 f}{\partial x \partial y} = f_{yx}\end{aligned}Keep in mind that these notations will only be valid when the limit exists for each condition. We can also apply a similar process to represent higher-order partial derivatives, but for now, let’s understand how we can calculate partial derivatives and second partial derivatives.

How To Do Partial Derivatives?

We can calculate partial derivatives by applying the definition of partial differentiation. Keep in mind that we only need to find the derivative of functions with respect to one variable by keeping the rest of the variables constant.Here are some pointers to remember when calculating first-order partial derivatives:
  • Identify the variable we’re differentiating. For example, when working with $\dfrac{\partial f}{\partial x}$, we different $f(x)$ with respect to $x$.
  • Treat the rest of the variables as constants.
  • Apply fundamental derivative rules to different $f(x)$ with respect to our variable.
This means that when we’re given $f(x, y) = 2x^2y – 4xy$, we can calculate their partial derivatives with respect to $x$ by treating $x$ as the sole variable and $y$ as a constant. Apply the appropriate derivative rules we need to simplify the expression.\begin{aligned}\dfrac{\partial f}{\partial {\color{Teal}x}} &=\dfrac{\partial }{\partial {\color{Teal}x}} (2{\color{Teal}x^2}y – 4{\color{Teal}x}y) \\&= 2 ({\color{Teal} 2x^{2 -1}})y – 4({\color{Teal}1})y\\&= 4xy – 4y  \end{aligned}We can use a similar process to evaluate $\dfrac{\partial f}{\partial y}$ – differentiate $f(x, y)$ with respect to $y$ and by treating $x$ as a constant.\begin{aligned}\dfrac{\partial f}{\partial {\color{DarkOrange}y}} &=\dfrac{\partial }{\partial {\color{DarkOrange}y}} (2x^2{\color{DarkOrange}y} – 4x{\color{DarkOrange}y}) \\&= 2x^2 ({\color{DarkOrange} 1}) – 4x({\color{DarkOrange}1})\\&= 2x^2 – 4x \end{aligned}Hence, the partial derivatives of $f(x, y)$ are:
  1. $\dfrac{\partial f}{\partial x} = f_x = 4xy – 4$
  2. $\dfrac{\partial f}{\partial y} = f_y = 2x^2 – 4x$
Now, let’s break down the steps of taking second order partial derivatives such as $\dfrac{\partial f}{\partial v_2 \partial v_1} = (f_{v_1})_{v_2}$.
  • Start differentiating $f(x)$ with respect to the first variable, $v_1$.
  • Differentiate the resulting expression with respect to $v_2$ and treating $v_1$ as constant.
Let us show you two examples on how we can evaluate second order partial derivatives: finding 1) $\dfrac{\partial^2 f}{\partial x^2}$ and 2) $\dfrac{\partial^2 f}{\partial x \partial y}$ of the function, $f(x, y) = 12x^2y – 3xy^2$.For the first problem, $\dfrac{\partial^2 f}{\partial x^2}$, we need to take the derivative of $f(x,y )$ with respect to $x$ twice. For two consecutive partial derivatives, we’ll consider $y$ as a constant and only work on differentiating terms with respect to $x$.\begin{aligned}\dfrac{\partial^2 f}{\partial x^2} &= \dfrac{\partial^2}{\partial x^2} (12x^2y – 3xy^2)\\&= \dfrac{\partial}{\partial x}\left[\dfrac{\partial}{\partial {\color{Teal}x}} (12{\color{Teal}x^2}y – 3{\color{Teal}x}y^2) \right] \\&= \dfrac{\partial}{\partial x} [12(2x)y – 3(1)y^2]\\&= \dfrac{\partial}{\partial x} (24xy – 3y^2)  \end{aligned}Now, differentiate the resulting expression with respect to $x$ once more.\begin{aligned}\dfrac{\partial}{\partial {\color{Teal}x}} (24{\color{Teal}x}y – 3y^2) &=  24({\color{Teal}1})y – {\color{Teal}0}\\&= 24y \end{aligned}This means that $\dfrac{\partial^2 }{\partial x^2} f(x, y)$ is equal to $24y$. When asked to determine $\dfrac{\partial^2 f}{\partial y^2}$, apply a similar process but this time, we’ll consider $x$ as the constant.Let’s now move on to $\dfrac{\partial^2 f}{\partial x \partial y}$ – it helps to rewrite $\dfrac{\partial^2 f}{\partial x \partial y}$ as $\dfrac{\partial}{\partial x}\left(\dfrac{\partial f}{\partial y}\right)$ to guide you in determining the order of the operation.\begin{aligned}\dfrac{\partial f}{\partial x \partial y} &= \dfrac{\partial }{\partial x} \left(\dfrac{\partial f}{\partial y} \right )\\&= \dfrac{\partial }{\partial x} \left[\dfrac{\partial }{\partial {\color{DarkOrange}y}} (12x^2{\color{DarkOrange}y} – 3x{\color{DarkOrange}y^2 })\right] \\&= \dfrac{\partial}{\partial x}[12x^2({\color{DarkOrange}1}) – 3x({\color{DarkOrange}2y})]\\&= \dfrac{\partial}{\partial x}(12x^2 – 6xy) \end{aligned}After differentiating $f(x, y)$ with respect to $y$, differentiate the resulting expression with respect to $x$.\begin{aligned}\dfrac{\partial}{\partial {\color{Teal}x}}(12{\color{Teal}x^2} – 6{\color{Teal}x}y) &= 12({\color{Teal}2x}) – 6y({\color{Teal}1}) \\&= 24x – 6y\end{aligned}This example shows how we can apply the partial derivatives twice in a row to evaluate second-order partial derivatives. We can apply a similar process when evaluating multiple order partial derivatives, but we’ll leave that for you to work on in the section below!Example 1Use the formal definition of partial derivative to find $f_x(x, y)$ when we have the function, $f(x, y) = xy^2 + x^2y$. SolutionAs we have discussed earlier, we can define the partial derivative of a function in terms of limits as shown below.\begin{aligned}f_x(x, y) &= \lim_{h \rightarrow 0} \dfrac{f(x + h, y) – f(x, y)}{h}\end{aligned}Use this definition then simplify the numerator as shown below.\begin{aligned}f_x(x, y) &= \lim_{h \rightarrow 0} \dfrac{f(x + h, y)- f(x, y)}{h}\\ &= \lim_{h \rightarrow 0} \dfrac{(x + h)y^2 + (x + h)^2y- (xy^2 + x^2y)}{h}\\&= \lim_{h \rightarrow 0} \dfrac{(xy^2 + y^2h) + (x^2 + 2xh + h^2)y – xy^2 – x^2y}{h}\\&= \lim_{h \rightarrow 0} \dfrac{xy^2 + y^2h + x^2y + 2xhy + h^2y- xy^2 – x^2y}{h}\end{aligned}Cancel the common factor, $h$, shared by the numerator and denominator then evaluate the limit of the resulting expression as $h \rightarrow 0$.\begin{aligned}f_x(x, y) &=  \lim_{h \rightarrow 0}  y^2 + 2xy + hy\\&= y^2 + 2xy\end{aligned}This means that the partial derivative of $f(x, y)$ with respect to $x$ is equal to $y^2 + 2xy$.Example 2Determine all of the first-order partial derivatives of the following functions.a. $f(x, y) = x^3 – 2\sqrt{y} + \dfrac{5}{x} – 6$ b. $f(x, y, z) = x^2y + 6yz^2 – 6\sin x \cos y + 8xz$SolutionWe’re being asked to write down all of the first-order partial derivatives of each of the functions, so for our first function, we need to determine $\dfrac{\partial f}{\partial x}$ and $\dfrac{\partial f}{\partial y}$.
  • To calculate $\dfrac{\partial f}{\partial x}$ or $f_x(x, y)$, we’ll take the derivative of the function with respect to $x$ by treating $y$ as a constant.
  • Similarly, we can calculate $\dfrac{\partial f}{\partial y}$ or $f_y(x, y)$ by treating $x$ as a constant.
We’ll summarize the calculations for the two partial derivatives of $f(x, y)$ in this table. Apply the derivative rules we’ve learned in the past.
\begin{aligned}\boldsymbol{\dfrac{\partial f}{\partial x} = f_x(x, y)}\end{aligned}\begin{aligned}\dfrac{\partial }{\partial x} f(x, y) &= \dfrac{\partial f}{\partial {\color{Teal}x}}\left({\color{Teal}x^3} – 2\sqrt{y} + {\color{Teal}\dfrac{5}{x} }- 6 \right )\\&= ({\color{Teal}3x^2}) – 0 + ({\color{Teal}-5x^{-1 -1}}) – 0\\&= 3x^2 – 5x^{-2}\\&= 3x^2 – \dfrac{5}{x^2}\end{aligned}
\begin{aligned}\boldsymbol{\dfrac{\partial f}{\partial y} = f_y(x, y)}\end{aligned}\begin{aligned}\dfrac{\partial }{\partial x} f(x, y) &= \dfrac{\partial f}{\partial {\color{DarkOrange}y}}\left(0 – {\color{DarkOrange} 2\sqrt{y} } +\dfrac{5}{x} {\color{DarkOrange} – 6} \right )\\&= x^3 – \left({\color{DarkOrange}2 \cdot \dfrac{1}{2}y^{\frac{1}{2}-1}}\right) + 0 + ({\color{DarkOrange} 0})\\&=- y^{-\frac{1}{2}}\\&= -\dfrac{1}{\sqrt{y}}\end{aligned}
a. This means that the partial derivatives of $f(x, y)$ are: $f_x = 3x^2 – \dfrac{5}{x^2}$ and $f_y = -\dfrac{1}{\sqrt{y}}$.For the second item, we’re now working with three components, so we’re expecting three partial derivatives. Apply the same process – taking the derivative with respect to $x$, $y$, or $z$ then treating the rest of the variables constant.Here’s a summary of our calculation for all three partial derivatives:
\begin{aligned}\boldsymbol{\dfrac{\partial f}{\partial x} = f_x(x, y, z)}\end{aligned}\begin{aligned}\dfrac{\partial }{\partial x} f(x, y, z) &= \dfrac{\partial f}{\partial {\color{Teal}x}} ({\color{Teal}x^2}y + 6yz^2 – 6{\color{Teal}\sin x} \cos y + {\color{Teal}8x}z)\\&= ({\color{Teal} 2x})y + 0 – 6({\color{Teal}}\cos x)\cos y + ({\color{Teal}8 \cdot 1})z\\&= 2xy – 6 \cos x\cos y + 8z\end{aligned}
\begin{aligned}\boldsymbol{\dfrac{\partial f}{\partial y} = f_y(x, y, z)}\end{aligned}\begin{aligned}\dfrac{\partial }{\partial x} f(x, y, z) &= \dfrac{\partial f}{\partial {\color{DarkOrange}y}} (x^2{\color{DarkOrange}y} + {\color{DarkOrange}6y}z^2 – 6\sin x{\color{DarkOrange}\cos y}  + 8xz)\\&= x^2({\color{DarkOrange} 1}) + 6({\color{DarkOrange}1})z^2 – 6\sin x \cdot{\color{DarkOrange}-\sin y} + 0\\&= x^2 + 6z^2 + 6\sin x \sin y\end{aligned}
\begin{aligned}\boldsymbol{\dfrac{\partial f}{\partial y} = f_z(x, y, z)}\end{aligned}\begin{aligned}\dfrac{\partial }{\partial x} f(x, y, z) &= \dfrac{\partial f}{\partial {\color{Purple}z}} (x^2y + 6y{\color{Purple}z^2 }- 6\sin x\cos y  + 8x{\color{Purple}z})\\&= 0 + 6y({\color{Purple}2z}) – 0 + 8x({\color{Purple}1})\\&= 12yz + 8x\end{aligned}
b. Hence, $f(x, y, z) = x^2y + 6yz^2 – 6\sin x \cos y + 8xz$ has the following partial derivatives: $f_x = 2xy – 6 \cos x\cos y + 8z$, $f_y = x^2 + 6z^2 + 6\sin x \sin y$, and $12yz + 8x $.Example 3Suppose that we have $f(x,y, z) = x^2y^4z – 2x^2y + 12xy^2z^2$, determine the following higher order partial derivatives:a. $\dfrac{\partial^2 f}{\partial y^2}$ b. $\dfrac{\partial^2 f}{\partial x \partial z}$ c. $\dfrac{\partial^3 f}{\partial y \partial x \partial z}$SolutionTo evaluate $\dfrac{\partial^2 f}{\partial y^2}$, we’ll need to differentiate $f(x, y, z)$ with respect to $y$ twice in a row. Treat both $x$ and $z$ as constant values as shown below.\begin{aligned}\dfrac{\partial^2 f}{\partial y^2}&= \dfrac{\partial }{\partial y}\left(\dfrac{\partial f}{\partial y} \right ) \\&= \dfrac{\partial }{\partial y}\left[\dfrac{\partial }{\partial y} (x^2y^4z – 2x^2y + 12xy^2z^2)  \right]\\&= \dfrac{\partial}{\partial y}\left[ x^2(4y^3)z – 2x^2(1) + 12xz^2(2y)\right]\\&= \dfrac{\partial}{\partial y}\left(4x^2y^3z – 2x^2 + 24xyz^2 \right )  \end{aligned}Repeat the process to find the expression for $\dfrac{\partial^2 f}{\partial y^2}$.\begin{aligned}\dfrac{\partial^2 f}{\partial y^2} &= \dfrac{\partial}{\partial y}\left(4x^2y^3z – 2x^2 + 24xyz^2 \right ) \\&= 4x^2(3y^2)z – 0 + 24xz^2(1)\\&= 12x^2y^2z + 24xz^2 \end{aligned}a. This means that $\dfrac{\partial^2 f}{\partial y^2}$ is equal to $12x^2y^2z + 24xz^2$.For the next time, we’ll take the partial derivative of $f(x, y, z)$ with respect to $z$ first.\begin{aligned}\dfrac{\partial^2 f}{\partial x \partial z} &= \dfrac{\partial}{\partial x}\left[\dfrac{\partial}{\partial z} (x^2y^4z – 2x^2y + 12xy^2z^2) \right] \\&= \dfrac{\partial}{\partial x} \left[x^2y^4 (1) – 0 + 12xy^2(2z) \right ]\\&= \dfrac{\partial}{\partial x}\left(x^2y^4 + 24xy^2z \right ) \end{aligned}Now, differentiate the resulting expression with respect to $x$.\begin{aligned}\dfrac{\partial^2 f}{\partial x \partial z} &= \dfrac{\partial}{\partial x}\left(x^2y^4 + 24xy^2z \right )\\&= y^4(2x) + 24yz(1)\\&= 2y^4x + 24y^2z \end{aligned}b. Hence, $\dfrac{\partial^2 f}{\partial x \partial z}$ is equivalent to $2y^4x + 24y^2z$.We can rewrite $\dfrac{\partial^3 f}{\partial y \partial x \partial z}$ as $\dfrac{\partial}{\partial y} \left(\dfrac{\partial^2 f}{\partial x \partial z} \right)$, so let’s use our result from the Q3b then differentiate it with respect to $y$.\begin{aligned}\dfrac{\partial^3 f}{\partial y \partial x \partial z} &= \dfrac{\partial}{\partial y}\left( \dfrac{\partial^2 f}{\partial x \partial z}\right ) \\ &= \dfrac{\partial}{\partial y} (2y^4x + 24y^2z ) \\&= 2x(4y^3) + 24z(2y)\\&= 8xy^3 + 48yz\end{aligned}c. This means that $\dfrac{\partial^3 f}{\partial y \partial x \partial z}$ is equal to $8xy^3 + 48yz$.

Practice Question

1. Use the formal definition of partial derivative to find $f_y(x, y)$ when we have the function, $f(x, y) = x^2 – 2xy + y^2$.2. Determine all of the first-order partial derivatives of the following functions. a. $f(x, y) = 2y^2 – 3\sqrt{x} + 4xy^2 – \dfrac{x}{y}$ b. $f(x, y, z) = x – 6xyz + y\sin x\cos z – \sqrt{yz}$ c. $f(x, y,z) = \sin(x^3y + z) – \cos(y^2 – xz)$3. Suppose that we have $f(x,y, z) = -3x^2y + 3xyz – 4y^2z^2 + 6\sin x \cos z$, determine the following higher order partial derivatives: a. $\dfrac{\partial^2 f}{\partial x^2}$ b. $\dfrac{\partial^2 f}{\partial y \partial z}$ c. $\dfrac{\partial^3 f}{\partial x \partial y \partial z}$

Answer Key

1. $ \begin{aligned}f_y(x, y) &= \lim_{h \rightarrow 0} \dfrac{[x^2 – 2x(y + h) + (y + h)^2] – (x^2 – 2xy + y^2)}{h}\\&= \lim_{h \rightarrow 0} \dfrac{(x^2 – 2xy – 2hx + y^2 + 2yh + h^2 – x^2 + 2xy – y^2)}{h}\\&=\lim_{h \rightarrow 0} \dfrac{(- 2hx + 2yh + h^2)}{h}\\&=\lim_{h \rightarrow 0} -2x + 2y + h\\&= -2x + 2y\end{aligned}$ 2. a. $f_x = 4y^2- \dfrac{1}{y}- \dfrac{3}{2\sqrt{x}}$, $f_y = y+ 8yx+ \dfrac{x}{y^2}$ b. $f_x = y\cos x \cos z – 6yz +1$, $f_y = -6xz+\sin x \cos z- \dfrac{\sqrt{z}}{2\sqrt{y}}$, $f_z = -6xy- y\sin x \sin z- \dfrac{\sqrt{y}}{2\sqrt{z}}$ c. $f_x = \cos \left(x^3y +z\right) \cdot \:3yx^2 – z\sin \left(y^2 – zx\right)$, $f_y = x^3 \cos \left(x^3y + z\right) + 2y\sin \left(y^2 – xz\right)$, $f_z = \cos \left(x^3y + z\right) – x\sin \left(y^2 – xz\right)$ 3. a. $\dfrac{\partial^2 f}{\partial x^2} = -6y – 6\sin x\cos z$ b. $\dfrac{\partial^2 f}{\partial y \partial z} = 3x – 16yz$ c. $\dfrac{\partial^3 f}{\partial x \partial y \partial z} = 3$3D images/mathematical drawings are created with GeoGebra.