JUMP TO TOPIC
Tautology – Definition and Examples
A tautology is a logical statement that must be true under any and all circumstances.
Mathematical proofs rely on tautologies. If they were built on statements that could be false, there would be exceptions to mathematical rules.
All branches of mathematics rely on tautologies. They are especially important to logic, though.
This section covers:
- What is a Tautology?
- Tautology Definition
- Tautology Example
What Is a Tautology?
A tautology is a statement that is always true.
In everyday language, tautology is a redundant statement like “it is what it is.” Clearly, this statement is always true.
Mathematically, however, tautologies are logical statements that are true regardless of the subject.
To better understand this, it is helpful to look at statements that are not tautologies.
A classic example of a statement that is not a tautology is “If \$P\$, then not \$P\$. In formal logic, this statement is $P \rightarrow \neg P$.
In this case, $P$ is an event, like “even number” or “rain” or “fish.”
Then it doesn’t make sense to say, “If $P$, then not $P$.” How can something simultaneously be an even number and not an even number? How can it be raining and not raining at once? Lastly, how can an animal be a fish and not a fish?
Statements that are sometimes, but not always, true are also not tautologies. An example of this is “$P$ implies $Q$.”
If this statement were a tautology, it would be true regardless of whether $P$ was true or $Q$ was true. That is not the case.
It is required to use a truth table to show this.
Truth Table
A truth table is a table that analyzes a logical statement to determine the circumstances for which it is true. The left side includes a column for each event in the statement, and the right side includes the final statement.
Sometimes, there are intermediary columns for sub-statements within the final statement. For example, the statement $(\neg P \cup \neg Q) \cup (P \cup Q)$ (read “not $P$ or not $Q$ or $P$ or $Q$) would include columns for $P$, $Q$, $\neg P \cup \neg Q$, $P \cup Q$, and $(\neg P \cup \neg Q) \cup (P \cup Q)$.
In the case of $P \rightarrow Q$, however, only three columns ($P$, $Q$, and $P \rightarrow Q$) are necessary.

If $P \rightarrow Q$, then it is possible to have situations where $P$ and $Q$ are both true or both false (the top and bottom rows).
It is also possible to have a situation where $P$ is false, but $Q$ is still true. Think, for example, of the statement, “If it is a cat, then it is a mammal.” In this case, $P$ is “cat,” and $Q$ is “mammal.” Clearly, there are mammals other than cats, such as dogs, etc.
However, it is impossible to have $P$ but not $Q$ if $P \rightarrow Q$. Thus, $P \rightarrow Q$ is not a tautology. Its truth depends on the statements given.
Tautology Definition
A tautology is a logical statement that is always true regardless of its component parts’ true or false values.
Each tautology will consist of one or more events, $P_k$. If $P_1,$ …, $P_n$ are true, then the tautology is true. If $P_1,$ …, $P_n$ are false, then the tautology is still true. And if there is any combination of true and false among the $P_k$ events, the tautology is still true.
Tautology Example
The simplest example of tautology is $P \cup \neg P$, which is read as “$P$ or not $P$.”
In logic, all events are either true or false. There is no in-between. Therefore, it makes intuitive sense that an event $P$ either is or is not.
In this truth table, there is only one event, $P$. There is also the sub-event, $\neg P$, and the statement itself, $P \cup \neg P$. Therefore, it is just a $3 \times 3$ table.

In this case, the truth value of $\neg P$ depends on the truth value of $P$. Therefore, it is impossible for both $P$ and $\neg P$ to have the same truth value.
Thus, the only two options are that $P$ is true or $P$ is false. When $P$ is true, $P \cup \neg P$ is true. When $P$ is false, $\neg P$ is true so $P \cup\neg P$ is still true.
Thus, whether $P$ is true or false, $P \cup \neg P$ is true. This means $P \cup \neg P$ is a tautology.
Examples
This section covers common examples of tautologies and their step-by-step solutions.
Example 1
Use the given truth table to determine whether the relationship $(Q \rightarrow P) \cup (P \rightarrow Q)$ is a tautology or not.

Solution
A tautology is true under any and all circumstances. Therefore, in a truth table, the tautology will always be true. That is, all the columns below it will have a “T.”
In this case, $(Q \rightarrow P) \cup (P \rightarrow Q)$ has all T’s beneath it. That is, it is always true that either $Q \rightarrow P$ is true, $P \rightarrow Q$ is true, or both.
Example 2
“On Saturday, I will either see a play or go to dinner and see a play.”
Convert this sentence into logical notation. Does it denote a tautology? Why or why not?
Solution
There are two events here. The first is “I will see a play on Saturday.” The second is “I will go to dinner on Saturday.”
Let the first event, “I will see a play on Saturday,” be $P$. Let the second event, “I will go to dinner on Saturday,” be $Q$.
Then, the relationship is $P \cup (P \cap Q)$.
If $P$ is true, the relationship is true.
But, if $P$ is false, both $P$ and $P \cap Q$ are false. That is, the statement $P \cup (P \cap Q)$ is false.
Therefore, the statement is not a tautology.
The truth table for this relationship looks like this:
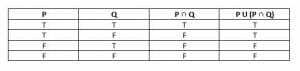
Example 3
Create a truth table for $(P \cup Q) \cup \neg P$. Is $(P \cup Q) \cup \neg P$ a tautology?
Solution
If $P$ is true, $P \cup Q$ is also true.
If $P$ is false, $\neg P$ is true.
Therefore, this statement is always true. The truth table is below.

Note that this is essentially the same as $P \cup \neg P$ with an extraneous event, $Q$ added in.
Example 4
The statement $(P \rightarrow Q) \cup (\neg Q \rightarrow \neg P)$ is not a tautology. Explain why using real events.
Solution
Let $P$ be the event “it is a fish,” and $Q$ be the event “it swims” as before.
This statement is false when $P$ is true, and $Q$ is false. In this case, “it is a fish, but it does not swim.” It is impossible then for it being a fish to imply it swims.
Likewise, the statement, “it does not swim, so it is not a fish,” also does not hold. Remember that $P$ being true and $Q$ being false translates to “it is a fish, but it does not swim.” These two statements are contradictions. Thus, $\neg Q \rightarrow \neg P$ is also false when $P$ is true, and $Q$ is false.
Therefore, both statements are false, so $(P \rightarrow Q) \cup (\neg Q \rightarrow \neg P)$ is false.
Example 5
Create a truth table for $P \rightarrow Q \cap Q \rightarrow P$. Is this a tautology?
Solution
As above, this statement is not a tautology. In fact, it is only true when $P$ and $Q$ have the same truth values.
It also represents a common logical fallacy that a first thing implies a second, so the second implies the first.
Here is the truth table for this situation.

The statements $P \rightarrow Q$ and $Q \rightarrow P$ are both true only when $P$ and $Q$ have the same truth value. Therefore, it is not a tautology.
Practice Problems
- Show that $(P \rightarrow \neg P) \cup (\neg P \rightarrow P)$ is a tautology using truth tables.
- Show that the statement “P and Q are both true or P and Q are both false” is not a tautology. Then, illustrate this with a real-world example.
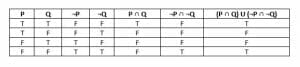
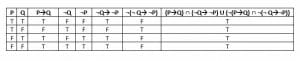
- If a conditional statement $P \rightarrow Q$ is true, then so is its contrapositive, $\neg Q \rightarrow \neg P$. Prove this by showing $P \rightarrow Q \cap \neg P \rightarrow \neg Q \cup \neg (P \rightarrow Q) \cap \neg (\neg Q \rightarrow \neg P)$.
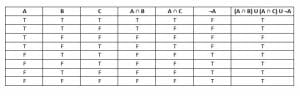
- If $A, B,$ and $C$ are events, is $(A \cap B) \cup (A \cap C) \cup \neg A)$ a tautology?
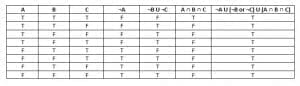
- If $A, B,$ and $C$ are events, is $\neg A \cup (\neg B \cup \neg C) \cup (A \cap B \cap C)$ a tautology?
Answer Key


Consider a situation where P is “Cat” and Q is “mammal.” P and Q can happen, but Q can still be true if P is false (say, a dog).


This is not a tautology because the statement is not true when $A$ is true, but $B$ and $C$ are false.

Yes, because the statement is true regardless of whether $A$, $B$, and $C$ are true.