Triangle Inequality – Explanation & Examples
In this article, we will learn what the triangle inequality theorem is, how to use the theorem, and lastly, what reverse triangle inequality entails. At this point, most of us are familiar with the fact that a triangle has three sides.
The three sides of a triangle are formed when three different line segments join at the vertices of a triangle. In a triangle, we use the small letters a, b and c to denote a triangle’s sides.
In most cases, letter a and b are used to represent the first two short sides of a triangle, whereas letter c is used to represent the longest side.
What is Triangle Inequality Theorem?
As the name suggests, the triangle inequality theorem is a statement that describes the relationship between the three sides of a triangle. According to the triangle inequality theorem, the sum of any two sides of a triangle is greater than or equal to the third side of a triangle.
This statement can symbolically be represented as;
- a + b > c
- a + c > b
- b + c > a
Therefore, a triangle inequality theorem is a useful tool for checking whether a given set of three dimensions will form a triangle or not. Simply put, it will not form a triangle if the above 3 triangle inequality conditions are false.
Let’s take a look at the following examples:
Example 1
Check whether it is possible to form a triangle with the following measures:
4 mm, 7 mm, and 5 mm.
Solution
Let a = 4 mm. b = 7 mm and c = 5 mm. Now apply the triangle inequality theorem.
a + b > c
⇒ 4 + 7 > 5
⇒ 11> 5 ……. (true)
a + c > b
⇒ 4 + 5 > 7
⇒ 9 > 7…………. (true)
b + c > a
⇒7 + 5 > 4
⇒12 > 4 ……. (true)
Since all three conditions are true, it is possible to form a triangle with the given measurements.
Example 2
Given the measurements; 6 cm, 10 cm, 17 cm. Check if the three measurements can form a triangle.
Solution
Let a = 6 cm, b = 10 cm and c = 17 cm
By triangle inequality theorem, we have;
a + b > c
⇒ 6 + 10 > 17
⇒ 16 > 17 ………. (false, 17 is not less than 16)
a + c > b
⇒ 6 + 17 > 10
⇒ 23 > 10…………. (true)
b + c > a
10 + 17 > 6
17 > 6 ………. (true)
Since one of the conditions is false, therefore, the three measurements cannot form a triangle.
Example 3
Find the possible values of x for the triangle shown below.
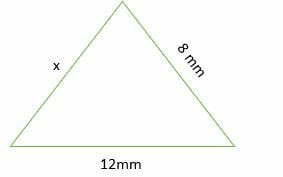
Solution
Using the triangle inequality theorem, we get;
⇒ x + 8 > 12
⇒ x > 4
⇒ x + 12 > 8
⇒ x > –4 ……… (invalid, lengths can never be negative numbers)
12 + 8 > x
⇒ x < 20 Combine the valid statements x > 4 and x < 20.
4 < x < 20
Therefore, the possible values of x are; 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 and 19.
Example 4
The dimensions of a triangle are given by (x + 2) cm, (2x+7) cm, and (4x+1). Find the possible values of x that are integers.
Solution
By the triangle inequality theorem; let a = (x + 2) cm, b = (2x+7) cm and c = (4x+1).
(x + 2) + (2x + 7) > (4x + 1)
3x + 9 > 4x + 1
3x – 4x > 1 – 9
– x > – 8
Divide both sides by – 1 and reverse the direction of the inequality symbol.
x < 8 (x + 2) + (4x +1) > (2x + 7)
5x + 3 > 2x + 7
5x – 2x > 7 – 3
3x > 4
Divide both sides by 3 to get;
x > 4/3
x > 1.3333.
(2x + 7) + (4x + 1) > (x + 2)
6x + 8 > x + 2
6x – x > 2 – 8
5x > – 6
x > – 6/5 …………… (impossible)
Combine the valid inequalities.
1.333 < x <8
Therefore, the possible integer values of x are 2, 3, 4, 5, 6, and 7.
Reverse Triangle Inequality
According to reverse triangle inequality, the difference between two side lengths of a triangle is smaller than the third side length. In other words, any side of a triangle is larger than the subtracts obtained when the remaining two sides of a triangle are subtracted.
Consider triangle PQR below;
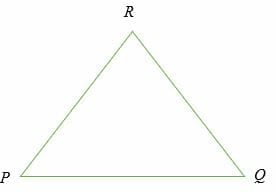
The reverse triangle inequality theorem is given by;
|PQ|>||PR|-|RQ||, |PR|>||PQ|-|RQ|| and |QR|>||PQ|-|PR||
Proof:
- |PQ| + |PR| > |RQ| // Triangle Inequality Theorem
- |PQ| + |PR| -|PR| > |RQ|-|PR| // (i) Subtracting the same quantity from both side maintains the inequality
- |PQ| > |RQ| – |PR| = ||PR|-|RQ|| // (ii), properties of absolute value
- |PQ| + |PR| – |PQ| > |RQ|-|PQ| // (ii) Subtracting the same quantity from both side maintains the inequality
- |PR| > |RQ|-|PQ| = ||PQ|-|RQ|| // (iv), properties of absolute value
- |PR|+|QR| > |PQ| //Triangle Inequality Theorem
- |PR| + |QR| -|PR| > |PQ|-|PR| // (vi) Subtracting the same quantity from both side maintains the inequality
- |QR| > |PQ| – |PR| = ||PQ|-|PR|| // (vii), properties of absolute value
