JUMP TO TOPIC
Types of Numbers – Difference and Classification
 Can you imagine how your life would be if you didn’t have any way to represent ages, weight, birthdays, time, scores, bank accounts, and telephone numbers? The ten mathematical digits (0 to 9) are used to define all of these quantities.
Can you imagine how your life would be if you didn’t have any way to represent ages, weight, birthdays, time, scores, bank accounts, and telephone numbers? The ten mathematical digits (0 to 9) are used to define all of these quantities.
Numbers are strings of digits used to represent a quantity. The magnitude of a number indicates the size of the quantity. It can be either large or small. They exist in different forms, such as 3, 999, 0.351, 2/5, etc.
Types of Numbers in Math
Just like different family members live in different homes, different numbers are of the same family but have different types. Over time, different patterns of ten digits have been classified into a variety of number types. These patterns of numbers are different from each other due to different representations and properties.
Natural Numbers
Natural numbers or counting numbers are the most basic types of numbers you learned for the first time as toddlers. They start from 1 and go to infinity, i.e., 1, 2, 3, 4, 5, 6, and so on. They are also called positive integers. In the set form, they can be written as:
{1, 2, 3, 4, 5, …}
Natural numbers are represented by the symbol N.
Whole Numbers
Whole numbers are the set of natural numbers, including zero. This means they start from 0 and go up to 1, 2, 3, and so on, i.e.
{0, 1, 2, 3, 4, 5, …}
Whole numbers are represented by the symbol W.
Integers
Integers are the set of all whole numbers and the negatives of natural numbers. They contain all the numbers which lie between negative infinity and positive infinity. They can be positive, zero, or negative but cannot be written in decimal or fraction. Integers can be written in set form as
{…, -3, -2, -1, 0, 1, 2, 3, …}
We can say that all whole numbers and natural numbers are integers, but not all integers are natural numbers or whole numbers.
The symbol Z represents integers.
Fractions
A fraction represents parts of a whole piece. It can be written in the form a/b, where both a and b are whole numbers, and b can never be equal to 0. All fractions are rational numbers, but not all rational numbers are fractions.
Fractions are further reduced to proper and improper fractions. Improper fractions are ones in which the numerator is greater than the denominator while the opposite is true in proper functions, i.e., the denominator is greater than the numerator. Examples of proper fractions are 3/7 and 99/101, while 7/3 and 101/99 are improper fractions. This means the improper fractions are always greater than 1.
All terminating decimals and repeating decimals can be written as fractions. You can write the terminating decimal 1.25 as 125/100 = 5/4. A repeating decimal 0.3333 can be written as 1/3.
Rational Numbers
You can write rational numbers in fraction form. The word “rational” is derived from the word “ratio, ” as rational numbers are the two integers’ ratios. For example, 0.7 is a rational number because it can be written as 7/10. Other examples of rational numbers are -1/3, 2/5, 99/100, 1.57, etc.
Consider a rational number p/q, where p and q are two integers. Here, the numerator p can be any integer (positive or negative), but the denominator q can never be 0, as the fraction is undefined. Also, if q = 1, then the fraction is an integer.
The symbol Q represents rational numbers.
Irrational Numbers
Irrational numbers cannot be written in fraction form, i.e., they cannot be written as the ratio of the two integers. A few examples of irrational numbers are √2, √5, 0.353535…, π, and so on. You can see that the digits in irrational numbers continue for infinity with no repeating pattern.
The symbol Q represents irrational numbers.
Real Numbers
Real numbers are the set of all rational and irrational numbers. This includes all the numbers which can be written in decimal form. All integers are real numbers, but not all real numbers are integers. Real numbers include all the integers, whole numbers, fractions, repeating decimals, terminating decimals, and so on.
The symbol R represents real numbers.
Imaginary Numbers
Numbers other than real numbers are imaginary or complex numbers. When we square an imaginary number, it gives a negative result, which means it is a square root of a negative number, for example, √-2 and √-5. When we square these numbers, the results are -2 and -5. The square root of negative one is represented by the letter i, i.e.
i = √-1
Example 1
What is the square root of -16? Write your answer in terms of the imaginary number i.
Solution
- Step 1: Write the square root form.
√(-16)
- Step 2: Separate -1.
√(16 × -1)
- Step 3: Separate square roots.
√(16) × √(-1)
- Step 4: Solve the square root.
4 × √(-1)
- Step 5: Write in the form of i.
4i
Sometimes you get an imaginary solution to the equations.
Example 2
Solve the equation,
x2 + 2 = 0
Solution
- Step 1: Take the constant term on other side of the equation.
x2 = -2
- Step 2: Take the square root on both sides.
√x2 = +√-2 or -√-2
- Step 3: Solve.
x = √(2) × √(-1)
x = +√2i or -√2i
- Step 4: Verify the answers by plugging values in the original equation and see if we get 0.
x2 + 2
(+√2i)2 + 2 = -2 + 2 = 0 (as i = √-1 and square of i is -1)
(-√2i)2 + 2 = -2 + 2 = 0 (as i = √-1 and square of i is -1)
Just because their name is “imaginary” does not mean they are useless. They have many applications. One of the greatest applications of imaginary numbers is their use in electric circuits. The calculations of current and voltage are done in terms of imaginary numbers. These numbers are also used in complex calculus computations. In some places, the imaginary number is also represented by the letter j.
Complex Numbers
An imaginary number is combined with a real number to obtain a complex number. It is represented as a + bi, where the real part and b are the complex part of the complex number. Real numbers lie on a number line, while complex numbers lie on a two-dimensional flat plane.
Like imaginary numbers, complex numbers are also not useless. They are used in many applications like Signals and Systems and Fourier Transform.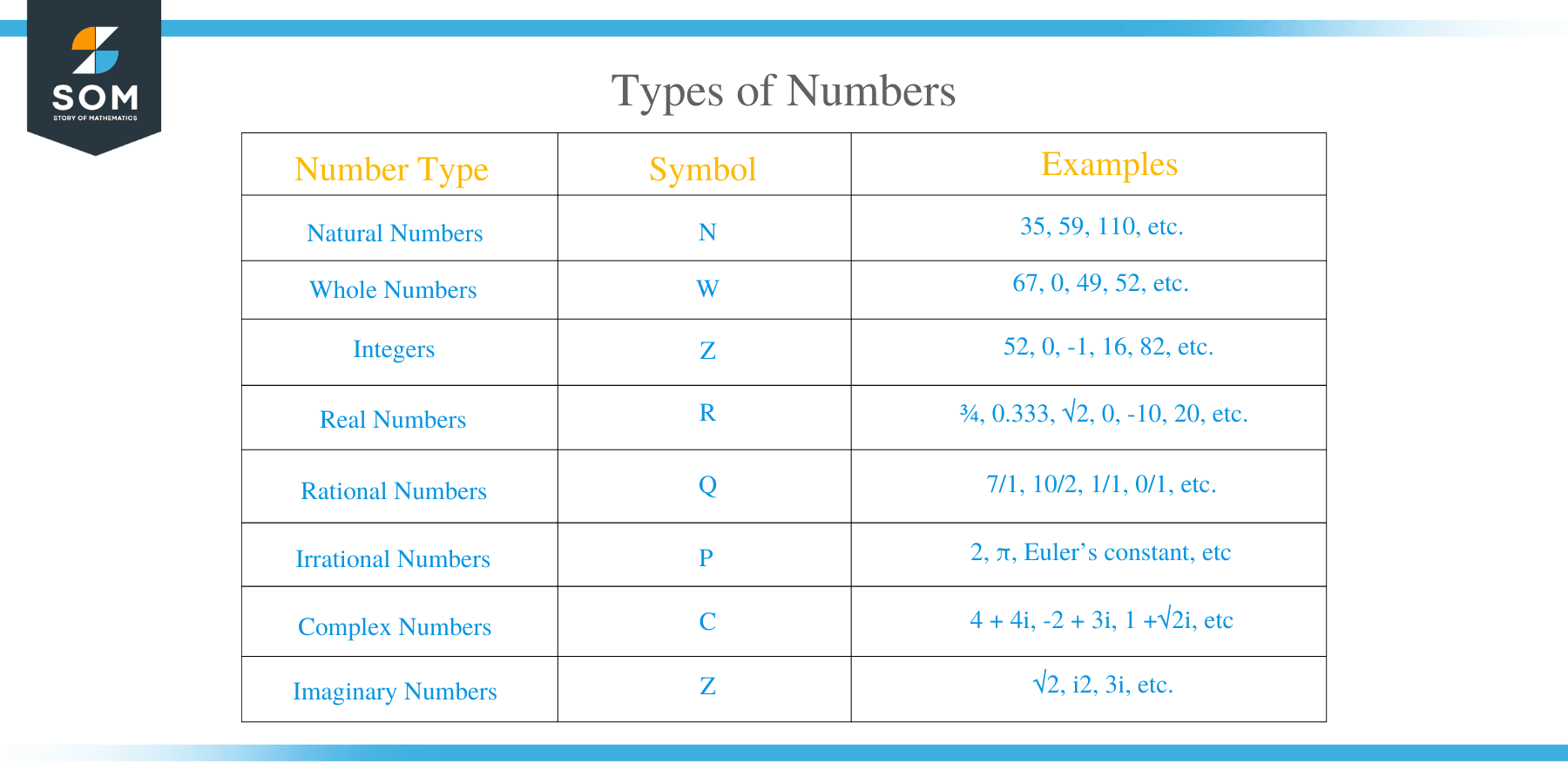
Prime Numbers and Composite Numbers
Prime and composite numbers are opposite of each other. Prime numbers are the type of integers with no factors other than themselves and 1, for example, 2, 3, 5, 7, and so on. The number 4 is not a prime number because it is divisible by 2. Similarly, 12 is also not a prime number because it is divisible by 2, 3, and 4. Therefore, 4 and 12 are the examples of composite numbers.
Transcendental Numbers
The numbers which can never be the zero (or root) of a polynomial equation with rational coefficients are called transcendental numbers. Not all irrational numbers are transcendental numbers, but all transcendental numbers are irrational numbers.
Classification of Numbers
The family of numbers we saw above can be classified in different categories as well. It is like a family has 20 members, but they live in two joint family houses of 10 members each, which means 10 members live in the same house. We can say two or more types of numbers can fall under one category.
Discrete and Continuous Numbers
The types of countable numbers are referred to as discrete numbers, and the types of numbers that cannot be counted are called continuous numbers. All natural numbers, whole numbers, integers, and rational numbers are discrete. This is because each of their sets is countable. The set of real numbers is too big and cannot be counted, so it is classified as continuous numbers. If we randomly take the two closest real numbers, there still exist infinitely more real numbers between them; hence they cannot be counted.
Sets of Numbers
Numbers can also be classified in the form of sets. Every type of number is a subset of another type of number. For example, natural numbers are the subset of whole numbers. Similarly, whole numbers are the subset of integers. The set of rational numbers contains all integers and fractions. The sets of rational numbers and irrational numbers form the real numbers. The real numbers fall under complex numbers with the imaginary part as 0. We can classify these numbers in a hierarchical chart as below:
Natural numbers can be further reduced to even, odd, prime, co-prime, composite, and perfect square numbers.
